A framework for compressing unstructured scientific data via serialization

We present a general framework for compressing unstructured scientific data with known local connectivity. A common application is simulation data defined on arbitrary finite element meshes. The framework employs a greedy topology preserving reordering of original nodes which allows for seamless integration into existing data processing pipelines. This reordering process depends solely on mesh connectivity and can be performed offline for optimal efficiency. However, the algorithm's greedy nature also supports on-the-fly implementation. The proposed method is compatible with any compression algorithm that leverages spatial correlations within the data. The effectiveness of this approach is demonstrated on a large-scale real dataset using several compression methods, including MGARD, SZ, and ZFP.

Dealing Doubt: Unveiling Threat Models in Gradient Inversion Attacks under Federated Learning, A Survey and Taxonomy

Federated Learning (FL) has emerged as a leading paradigm for decentralized, privacy preserving machine learning training. However, recent research on gradient inversion attacks (GIAs) have shown that gradient updates in FL can leak information on private training samples. While existing surveys on GIAs have focused on the honest-but-curious server threat model, there is a dearth of research categorizing attacks under the realistic and far more privacy-infringing cases of malicious servers and clients. In this paper, we present a survey and novel taxonomy of GIAs that emphasize FL threat models, particularly that of malicious servers and clients. We first formally define GIAs and contrast conventional attacks with the malicious attacker. We then summarize existing honest-but-curious attack strategies, corresponding defenses, and evaluation metrics. Critically, we dive into attacks with malicious servers and clients to highlight how they break existing FL defenses, focusing specifically on reconstruction methods, target model architectures, target data, and evaluation metrics. Lastly, we discuss open problems and future research directions.

MGARD: A multigrid framework for high-performance, error-controlled data compression and refactoring

We describe MGARD, a software providing MultiGrid Adaptive Reduction for floating-point scientific data on structured and unstructured grids. With exceptional data compression capability and precise error control, MGARD addresses a wide range of requirements, including storage reduction, high-performance I/O, and in-situ data analysis. It features a unified application programming interface (API) that seamlessly operates across diverse computing architectures. MGARD has been optimized with highly-tuned GPU kernels and efficient memory and device management mechanisms, ensuring scalable and rapid operations.

Spatiotemporally adaptive compression for scientific dataset with feature preservation -- a case study on simulation data with extreme climate events analysis

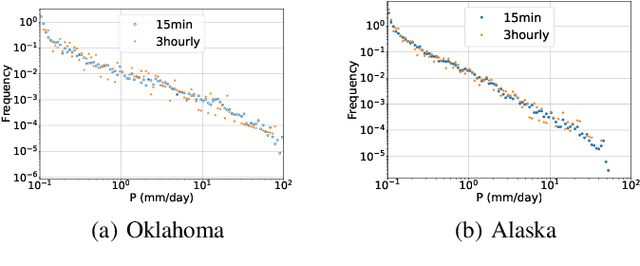
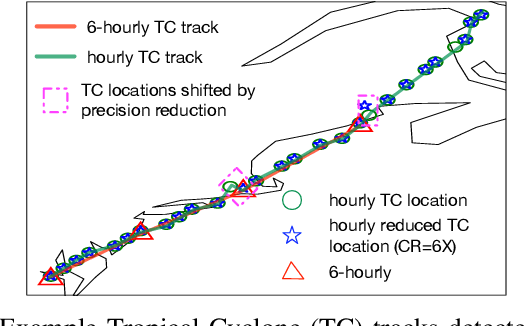
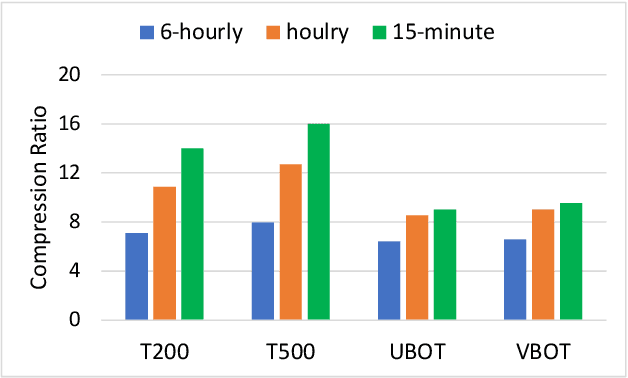
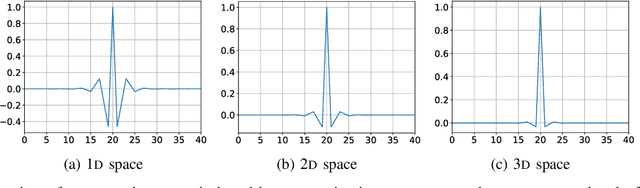
Scientific discoveries are increasingly constrained by limited storage space and I/O capacities. For time-series simulations and experiments, their data often need to be decimated over timesteps to accommodate storage and I/O limitations. In this paper, we propose a technique that addresses storage costs while improving post-analysis accuracy through spatiotemporal adaptive, error-controlled lossy compression. We investigate the trade-off between data precision and temporal output rates, revealing that reducing data precision and increasing timestep frequency lead to more accurate analysis outcomes. Additionally, we integrate spatiotemporal feature detection with data compression and demonstrate that performing adaptive error-bounded compression in higher dimensional space enables greater compression ratios, leveraging the error propagation theory of a transformation-based compressor. To evaluate our approach, we conduct experiments using the well-known E3SM climate simulation code and apply our method to compress variables used for cyclone tracking. Our results show a significant reduction in storage size while enhancing the quality of cyclone tracking analysis, both quantitatively and qualitatively, in comparison to the prevalent timestep decimation approach. Compared to three state-of-the-art lossy compressors lacking feature preservation capabilities, our adaptive compression framework improves perfectly matched cases in TC tracking by 26.4-51.3% at medium compression ratios and by 77.3-571.1% at large compression ratios, with a merely 5-11% computational overhead.

Dissipative residual layers for unsupervised implicit parameterization of data manifolds

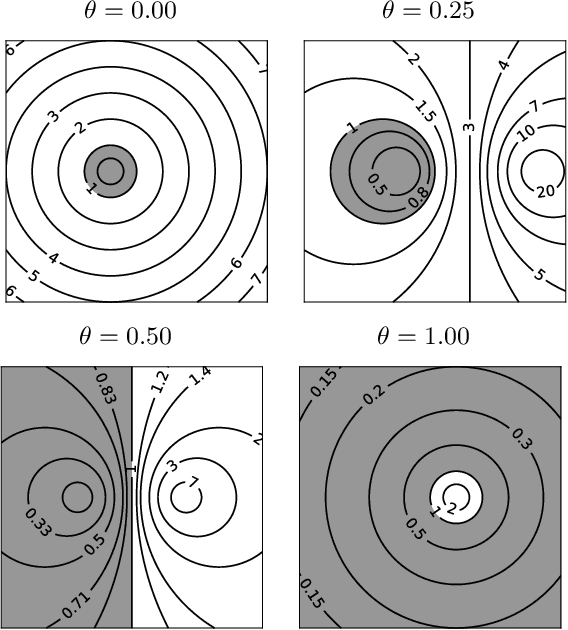
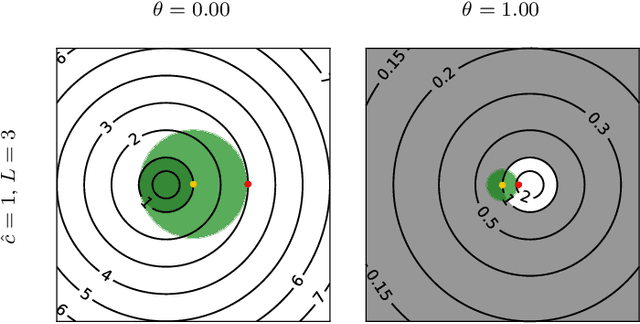
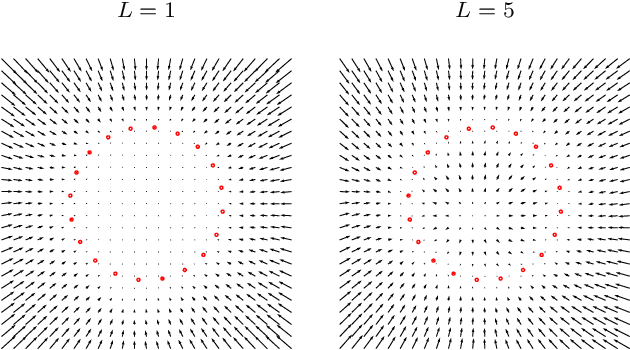
We propose an unsupervised technique for implicit parameterization of data manifolds. In our approach, the data is assumed to belong to a lower dimensional manifold in a higher dimensional space, and the data points are viewed as the endpoints of the trajectories originating outside the manifold. Under this assumption, the data manifold is an attractive manifold of a dynamical system to be estimated. We parameterize such a dynamical system with a residual neural network and propose a spectral localization technique to ensure it is locally attractive in the vicinity of data. We also present initialization and additional regularization of the proposed residual layers. % that we call dissipative bottlenecks. We mention the importance of the considered problem for the tasks of reinforcement learning and support our discussion with examples demonstrating the performance of the proposed layers in denoising and generative tasks.

Stable Anderson Acceleration for Deep Learning

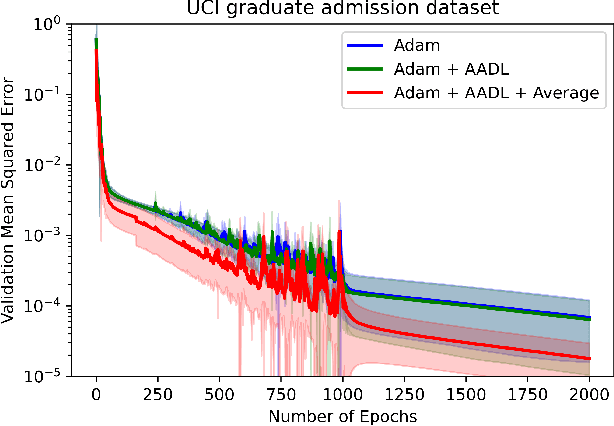
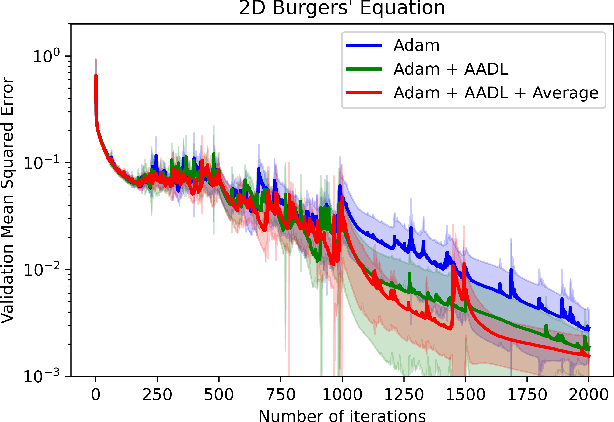
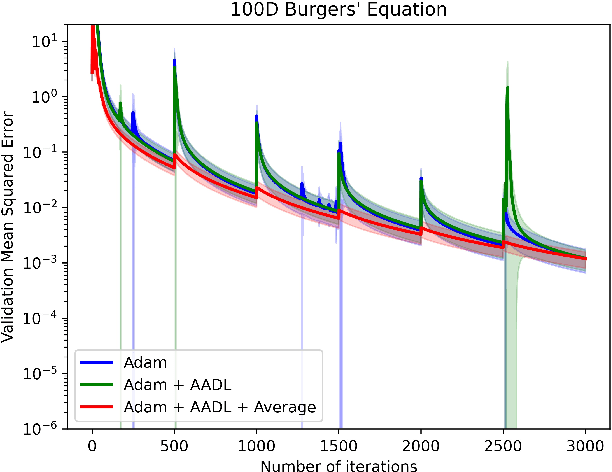
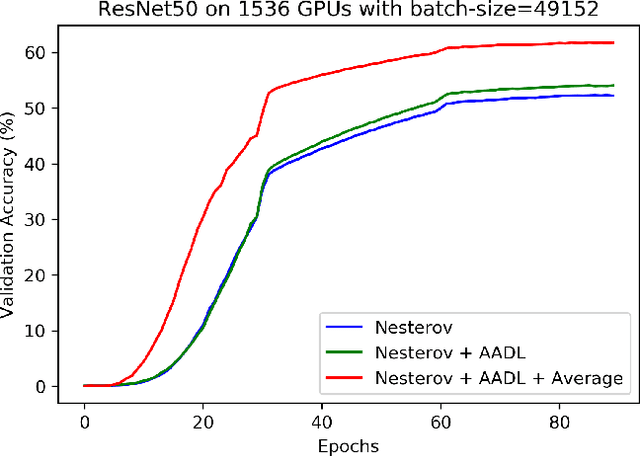
Anderson acceleration (AA) is an extrapolation technique designed to speed-up fixed-point iterations like those arising from the iterative training of DL models. Training DL models requires large datasets processed in randomly sampled batches that tend to introduce in the fixed-point iteration stochastic oscillations of amplitude roughly inversely proportional to the size of the batch. These oscillations reduce and occasionally eliminate the positive effect of AA. To restore AA's advantage, we combine it with an adaptive moving average procedure that smoothes the oscillations and results in a more regular sequence of gradient descent updates. By monitoring the relative standard deviation between consecutive iterations, we also introduce a criterion to automatically assess whether the moving average is needed. We applied the method to the following DL instantiations: (i) multi-layer perceptrons (MLPs) trained on the open-source graduate admissions dataset for regression, (ii) physics informed neural networks (PINNs) trained on source data to solve 2d and 100d Burgers' partial differential equations (PDEs), and (iii) ResNet50 trained on the open-source ImageNet1k dataset for image classification. Numerical results obtained using up to 1,536 NVIDIA V100 GPUs on the OLCF supercomputer Summit showed the stabilizing effect of the moving average on AA for all the problems above.

A nonlocal feature-driven exemplar-based approach for image inpainting

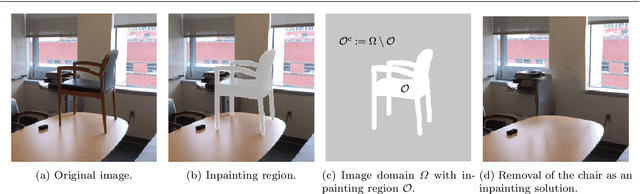
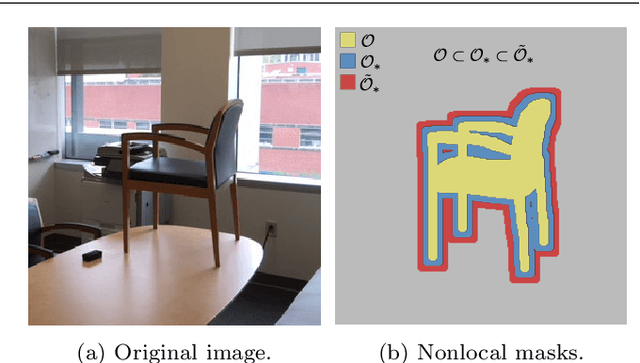
We present a nonlocal variational image completion technique which admits simultaneous inpainting of multiple structures and textures in a unified framework. The recovery of geometric structures is achieved by using general convolution operators as a measure of behavior within an image. These are combined with a nonlocal exemplar-based approach to exploit the self-similarity of an image in the selected feature domains and to ensure the inpainting of textures. We also introduce an anisotropic patch distance metric to allow for better control of the feature selection within an image and present a nonlocal energy functional based on this metric. Finally, we derive an optimization algorithm for the proposed variational model and examine its validity experimentally with various test images.

Robust learning with implicit residual networks

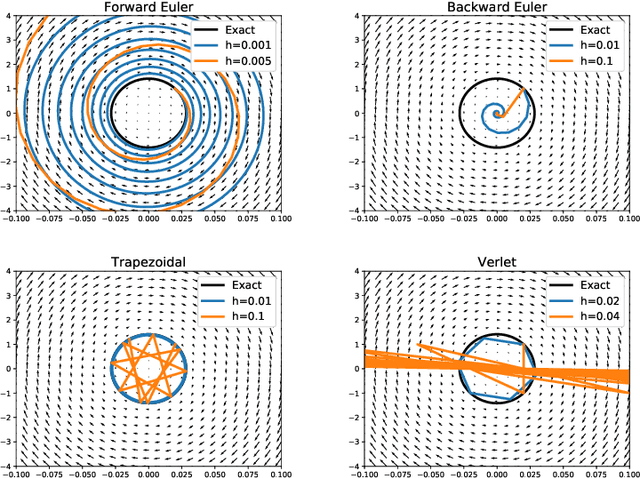
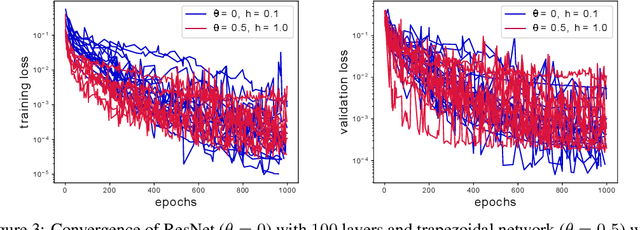
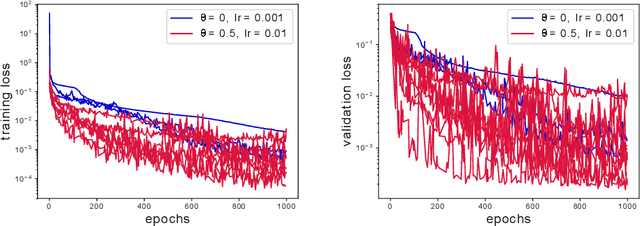
In this effort we propose a new deep architecture utilizing residual blocks inspired by implicit discretization schemes. As opposed to the standard feed-forward networks, the outputs of the proposed implicit residual blocks are defined as the fixed points of the appropriately chosen nonlinear transformations. We show that this choice leads to improved stability of both forward and backward propagations, has a favorable impact on the generalization power of the network and allows for higher learning rates. In addition, we consider a reformulation of ResNet which does not introduce new parameters and can potentially lead to a reduction in the number of required layers due to improved forward stability and robustness. Finally, we derive the memory efficient reversible training algorithm and provide numerical results in support of our findings.