Dissipative residual layers for unsupervised implicit parameterization of data manifolds
Paper and Code
Oct 13, 2022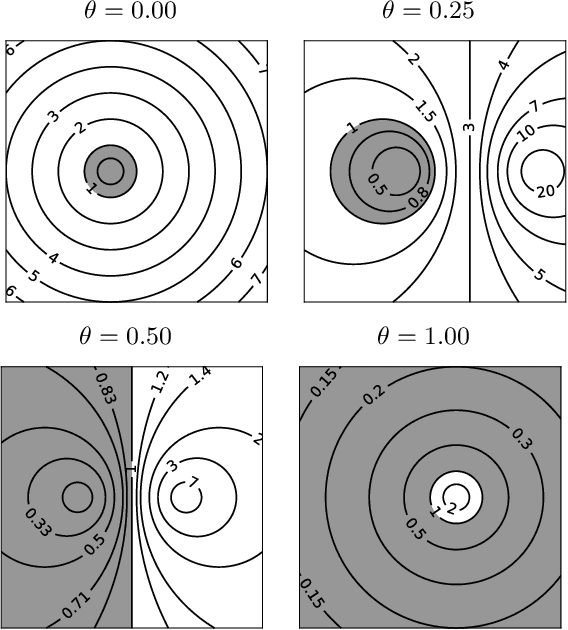
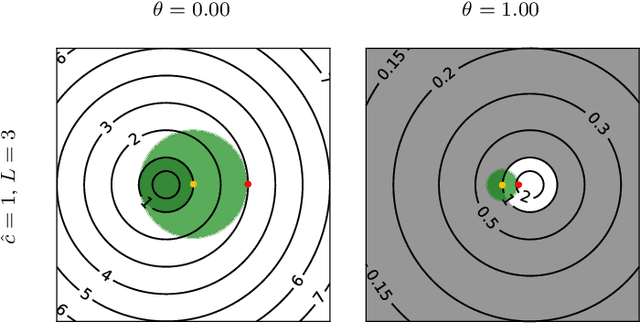
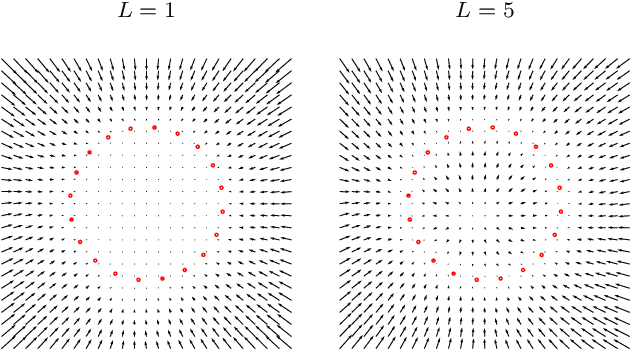

We propose an unsupervised technique for implicit parameterization of data manifolds. In our approach, the data is assumed to belong to a lower dimensional manifold in a higher dimensional space, and the data points are viewed as the endpoints of the trajectories originating outside the manifold. Under this assumption, the data manifold is an attractive manifold of a dynamical system to be estimated. We parameterize such a dynamical system with a residual neural network and propose a spectral localization technique to ensure it is locally attractive in the vicinity of data. We also present initialization and additional regularization of the proposed residual layers. % that we call dissipative bottlenecks. We mention the importance of the considered problem for the tasks of reinforcement learning and support our discussion with examples demonstrating the performance of the proposed layers in denoising and generative tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge