Increasing Entropy to Boost Policy Gradient Performance on Personalization Tasks

In this effort, we consider the impact of regularization on the diversity of actions taken by policies generated from reinforcement learning agents trained using a policy gradient. Policy gradient agents are prone to entropy collapse, which means certain actions are seldomly, if ever, selected. We augment the optimization objective function for the policy with terms constructed from various $\varphi$-divergences and Maximum Mean Discrepancy which encourages current policies to follow different state visitation and/or action choice distribution than previously computed policies. We provide numerical experiments using MNIST, CIFAR10, and Spotify datasets. The results demonstrate the advantage of diversity-promoting policy regularization and that its use on gradient-based approaches have significantly improved performance on a variety of personalization tasks. Furthermore, numerical evidence is given to show that policy regularization increases performance without losing accuracy.

On the Unreasonable Efficiency of State Space Clustering in Personalization Tasks

In this effort we consider a reinforcement learning (RL) technique for solving personalization tasks with complex reward signals. In particular, our approach is based on state space clustering with the use of a simplistic $k$-means algorithm as well as conventional choices of the network architectures and optimization algorithms. Numerical examples demonstrate the efficiency of different RL procedures and are used to illustrate that this technique accelerates the agent's ability to learn and does not restrict the agent's performance.

Offline Policy Comparison under Limited Historical Agent-Environment Interactions

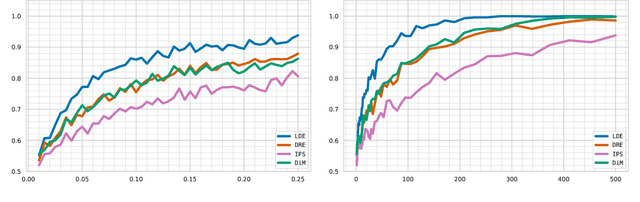
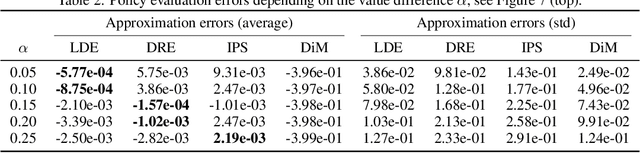
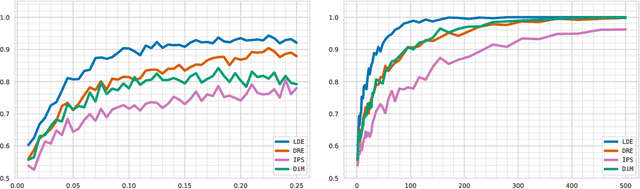
We address the challenge of policy evaluation in real-world applications of reinforcement learning systems where the available historical data is limited due to ethical, practical, or security considerations. This constrained distribution of data samples often leads to biased policy evaluation estimates. To remedy this, we propose that instead of policy evaluation, one should perform policy comparison, i.e. to rank the policies of interest in terms of their value based on available historical data. In addition we present the Limited Data Estimator (LDE) as a simple method for evaluating and comparing policies from a small number of interactions with the environment. According to our theoretical analysis, the LDE is shown to be statistically reliable on policy comparison tasks under mild assumptions on the distribution of the historical data. Additionally, our numerical experiments compare the LDE to other policy evaluation methods on the task of policy ranking and demonstrate its advantage in various settings.

Analysis of The Ratio of $\ell_1$ and $\ell_2$ Norms in Compressed Sensing

We first propose a novel criterion that guarantees that an $s$-sparse signal is the local minimizer of the $\ell_1/\ell_2$ objective; our criterion is interpretable and useful in practice. We also give the first uniform recovery condition using a geometric characterization of the null space of the measurement matrix, and show that this condition is easily satisfied for a class of random matrices. We also present analysis on the stability of the procedure when noise pollutes data. Numerical experiments are provided that compare $\ell_1/\ell_2$ with some other popular non-convex methods in compressed sensing. Finally, we propose a novel initialization approach to accelerate the numerical optimization procedure. We call this initialization approach \emph{support selection}, and we demonstrate that it empirically improves the performance of existing $\ell_1/\ell_2$ algorithms.

Analysis of Deep Neural Networks with Quasi-optimal polynomial approximation rates

We show the existence of a deep neural network capable of approximating a wide class of high-dimensional approximations. The construction of the proposed neural network is based on a quasi-optimal polynomial approximation. We show that this network achieves an error rate that is sub-exponential in the number of polynomial functions, $M$, used in the polynomial approximation. The complexity of the network which achieves this sub-exponential rate is shown to be algebraic in $M$.

Neural network integral representations with the ReLU activation function

We derive a formula for neural network integral representations on the sphere with the ReLU activation function under the finite $L_1$ norm (with respect to Lebesgue measure on the sphere) assumption on the outer weights. In one dimensional case, we further solve via a closed-form formula all possible such representations. Additionally, in this case our formula allows one to explicitly solve the least $L_1$ norm neural network representation for a given function.

Robust learning with implicit residual networks

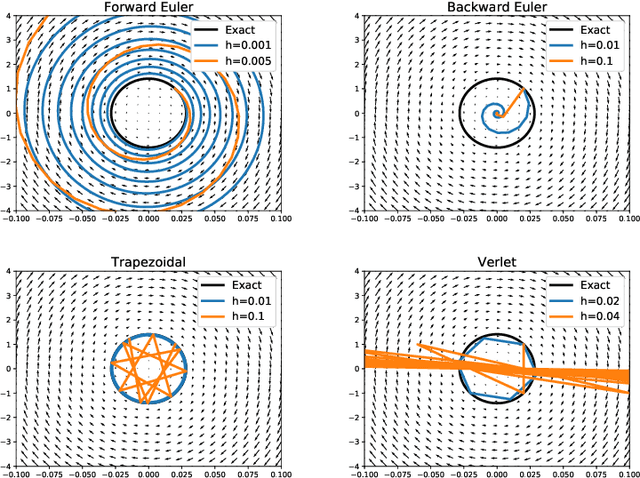
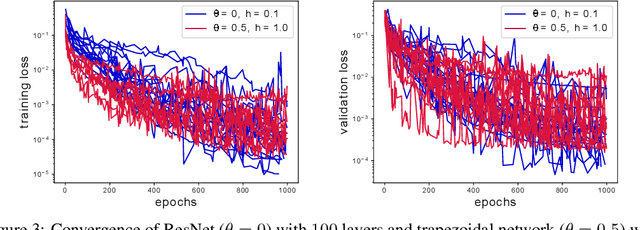
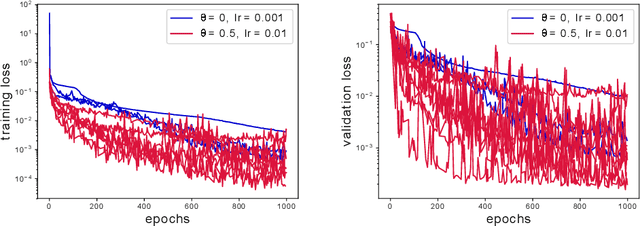
In this effort we propose a new deep architecture utilizing residual blocks inspired by implicit discretization schemes. As opposed to the standard feed-forward networks, the outputs of the proposed implicit residual blocks are defined as the fixed points of the appropriately chosen nonlinear transformations. We show that this choice leads to improved stability of both forward and backward propagations, has a favorable impact on the generalization power of the network and allows for higher learning rates. In addition, we consider a reformulation of ResNet which does not introduce new parameters and can potentially lead to a reduction in the number of required layers due to improved forward stability and robustness. Finally, we derive the memory efficient reversible training algorithm and provide numerical results in support of our findings.

Greedy Shallow Networks: A New Approach for Constructing and Training Neural Networks

We present a novel greedy approach to obtain a single layer neural network approximation to a target function with the use of a ReLU activation function. In our approach we construct a shallow network by utilizing a greedy algorithm where the set of possible inner weights acts as a parametrization of the prescribed dictionary. To facilitate the greedy selection we employ an integral representation of the network, based on the ridgelet transform, that significantly reduces the cardinality of the dictionary and hence promotes feasibility of the proposed method. Our approach allows for the construction of efficient architectures which can be treated either as improved initializations to be used in place of random-based alternatives, or as fully-trained networks, thus potentially nullifying the need for training and/or calibrating based on backpropagation. Numerical experiments demonstrate the tenability of the proposed concept and its advantages compared to the classical techniques for training and constructing neural networks.