Robust learning with implicit residual networks

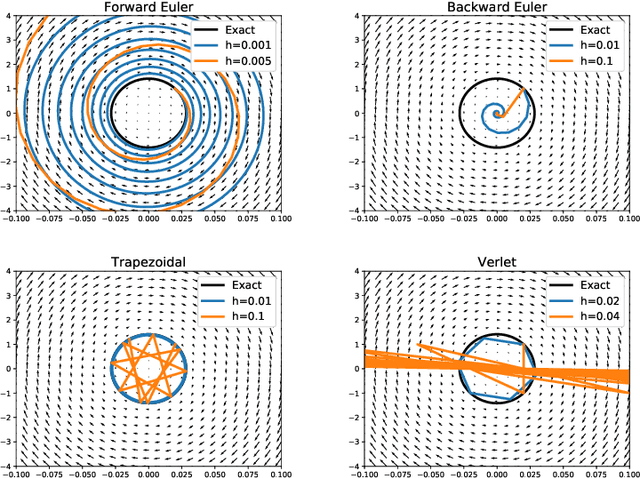
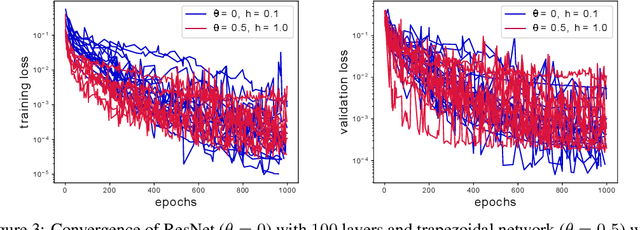
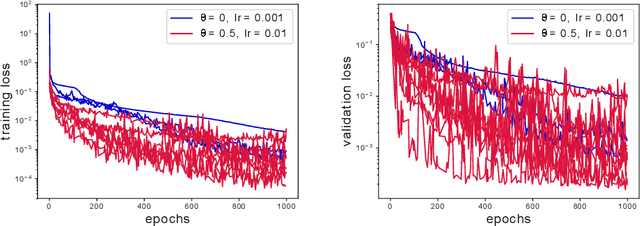
In this effort we propose a new deep architecture utilizing residual blocks inspired by implicit discretization schemes. As opposed to the standard feed-forward networks, the outputs of the proposed implicit residual blocks are defined as the fixed points of the appropriately chosen nonlinear transformations. We show that this choice leads to improved stability of both forward and backward propagations, has a favorable impact on the generalization power of the network and allows for higher learning rates. In addition, we consider a reformulation of ResNet which does not introduce new parameters and can potentially lead to a reduction in the number of required layers due to improved forward stability and robustness. Finally, we derive the memory efficient reversible training algorithm and provide numerical results in support of our findings.