Attention Based Machine Learning Methods for Data Reduction with Guaranteed Error Bounds

Scientific applications in fields such as high energy physics, computational fluid dynamics, and climate science generate vast amounts of data at high velocities. This exponential growth in data production is surpassing the advancements in computing power, network capabilities, and storage capacities. To address this challenge, data compression or reduction techniques are crucial. These scientific datasets have underlying data structures that consist of structured and block structured multidimensional meshes where each grid point corresponds to a tensor. It is important that data reduction techniques leverage strong spatial and temporal correlations that are ubiquitous in these applications. Additionally, applications such as CFD, process tensors comprising hundred plus species and their attributes at each grid point. Reduction techniques should be able to leverage interrelationships between the elements in each tensor. In this paper, we propose an attention-based hierarchical compression method utilizing a block-wise compression setup. We introduce an attention-based hyper-block autoencoder to capture inter-block correlations, followed by a block-wise encoder to capture block-specific information. A PCA-based post-processing step is employed to guarantee error bounds for each data block. Our method effectively captures both spatiotemporal and inter-variable correlations within and between data blocks. Compared to the state-of-the-art SZ3, our method achieves up to 8 times higher compression ratio on the multi-variable S3D dataset. When evaluated on single-variable setups using the E3SM and XGC datasets, our method still achieves up to 3 times and 2 times higher compression ratio, respectively.

Machine Learning Techniques for Data Reduction of Climate Applications

Scientists conduct large-scale simulations to compute derived quantities-of-interest (QoI) from primary data. Often, QoI are linked to specific features, regions, or time intervals, such that data can be adaptively reduced without compromising the integrity of QoI. For many spatiotemporal applications, these QoI are binary in nature and represent presence or absence of a physical phenomenon. We present a pipelined compression approach that first uses neural-network-based techniques to derive regions where QoI are highly likely to be present. Then, we employ a Guaranteed Autoencoder (GAE) to compress data with differential error bounds. GAE uses QoI information to apply low-error compression to only these regions. This results in overall high compression ratios while still achieving downstream goals of simulation or data collections. Experimental results are presented for climate data generated from the E3SM Simulation model for downstream quantities such as tropical cyclone and atmospheric river detection and tracking. These results show that our approach is superior to comparable methods in the literature.

MGARD: A multigrid framework for high-performance, error-controlled data compression and refactoring

We describe MGARD, a software providing MultiGrid Adaptive Reduction for floating-point scientific data on structured and unstructured grids. With exceptional data compression capability and precise error control, MGARD addresses a wide range of requirements, including storage reduction, high-performance I/O, and in-situ data analysis. It features a unified application programming interface (API) that seamlessly operates across diverse computing architectures. MGARD has been optimized with highly-tuned GPU kernels and efficient memory and device management mechanisms, ensuring scalable and rapid operations.

Scalable Hybrid Learning Techniques for Scientific Data Compression

Data compression is becoming critical for storing scientific data because many scientific applications need to store large amounts of data and post process this data for scientific discovery. Unlike image and video compression algorithms that limit errors to primary data, scientists require compression techniques that accurately preserve derived quantities of interest (QoIs). This paper presents a physics-informed compression technique implemented as an end-to-end, scalable, GPU-based pipeline for data compression that addresses this requirement. Our hybrid compression technique combines machine learning techniques and standard compression methods. Specifically, we combine an autoencoder, an error-bounded lossy compressor to provide guarantees on raw data error, and a constraint satisfaction post-processing step to preserve the QoIs within a minimal error (generally less than floating point error). The effectiveness of the data compression pipeline is demonstrated by compressing nuclear fusion simulation data generated by a large-scale fusion code, XGC, which produces hundreds of terabytes of data in a single day. Our approach works within the ADIOS framework and results in compression by a factor of more than 150 while requiring only a few percent of the computational resources necessary for generating the data, making the overall approach highly effective for practical scenarios.

Expressing linear equality constraints in feedforward neural networks

We seek to impose linear, equality constraints in feedforward neural networks. As top layer predictors are usually nonlinear, this is a difficult task if we seek to deploy standard convex optimization methods and strong duality. To overcome this, we introduce a new saddle-point Lagrangian with auxiliary predictor variables on which constraints are imposed. Elimination of the auxiliary variables leads to a dual minimization problem on the Lagrange multipliers introduced to satisfy the linear constraints. This minimization problem is combined with the standard learning problem on the weight matrices. From this theoretical line of development, we obtain the surprising interpretation of Lagrange parameters as additional, penultimate layer hidden units with fixed weights stemming from the constraints. Consequently, standard minimization approaches can be used despite the inclusion of Lagrange parameters -- a very satisfying, albeit unexpected, discovery. Examples ranging from multi-label classification to constrained autoencoders are envisaged in the future.

Hybrid Generative Models for Two-Dimensional Datasets

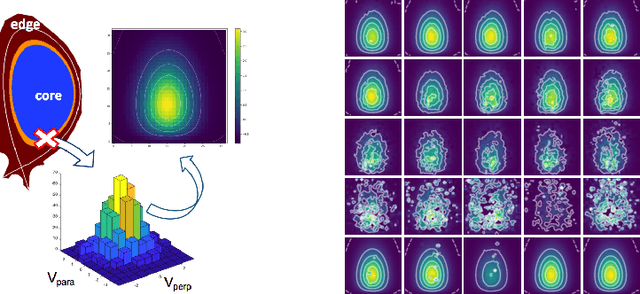
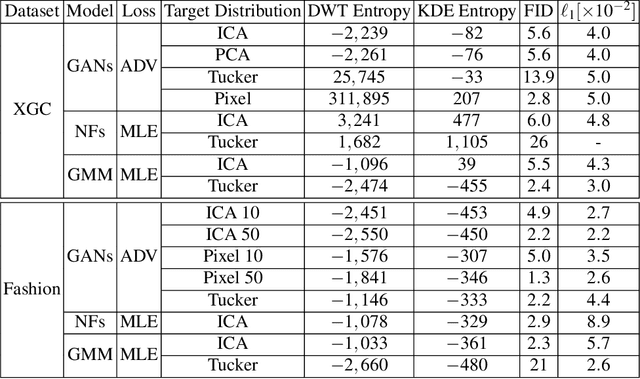
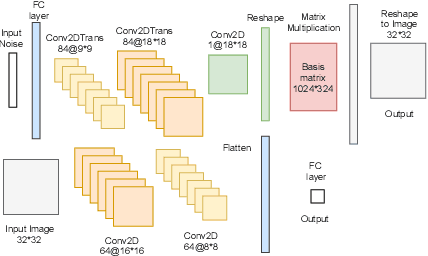
Two-dimensional array-based datasets are pervasive in a variety of domains. Current approaches for generative modeling have typically been limited to conventional image datasets and performed in the pixel domain which do not explicitly capture the correlation between pixels. Additionally, these approaches do not extend to scientific and other applications where each element value is continuous and is not limited to a fixed range. In this paper, we propose a novel approach for generating two-dimensional datasets by moving the computations to the space of representation bases and show its usefulness for two different datasets, one from imaging and another from scientific computing. The proposed approach is general and can be applied to any dataset, representation basis, or generative model. We provide a comprehensive performance comparison of various combinations of generative models and representation basis spaces. We also propose a new evaluation metric which captures the deficiency of generating images in pixel space.

A Hidden Variables Approach to Multilabel Logistic Regression

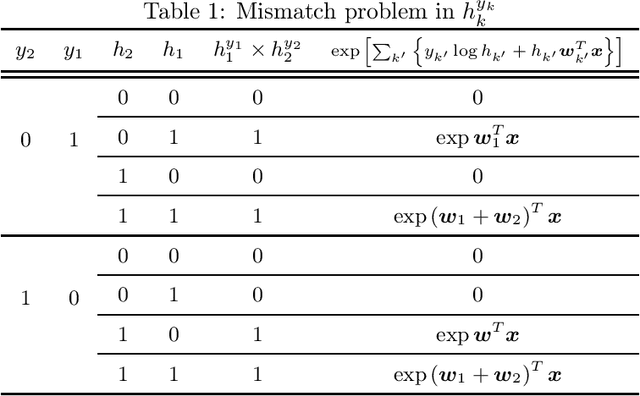
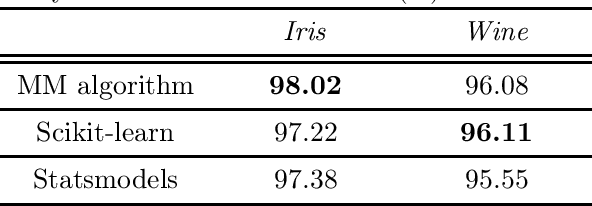
Multilabel classification is an important problem in a wide range of domains such as text categorization and music annotation. In this paper, we present a probabilistic model, Multilabel Logistic Regression with Hidden variables (MLRH), which extends the standard logistic regression by introducing hidden variables. Hidden variables make it possible to go beyond the conventional multiclass logistic regression by relaxing the one-hot-encoding constraint. We define a new joint distribution of labels and hidden variables which enables us to obtain one classifier for multilabel classification. Our experimental studies on a set of benchmark datasets demonstrate that the probabilistic model can achieve competitive performance compared with other multilabel learning algorithms.