Hybrid Generative Models for Two-Dimensional Datasets

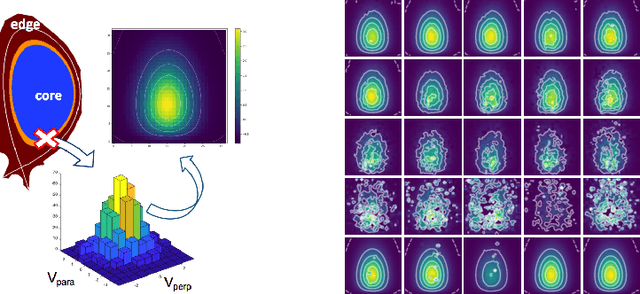
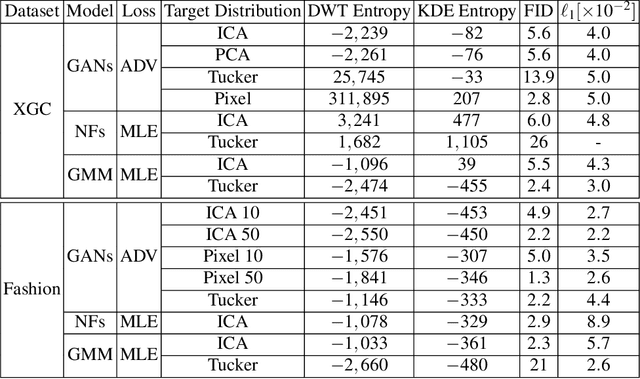
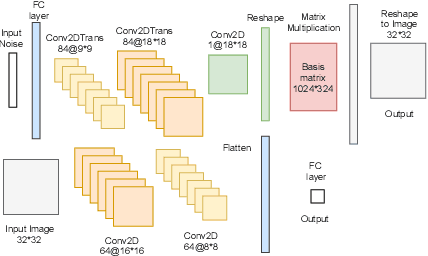
Two-dimensional array-based datasets are pervasive in a variety of domains. Current approaches for generative modeling have typically been limited to conventional image datasets and performed in the pixel domain which do not explicitly capture the correlation between pixels. Additionally, these approaches do not extend to scientific and other applications where each element value is continuous and is not limited to a fixed range. In this paper, we propose a novel approach for generating two-dimensional datasets by moving the computations to the space of representation bases and show its usefulness for two different datasets, one from imaging and another from scientific computing. The proposed approach is general and can be applied to any dataset, representation basis, or generative model. We provide a comprehensive performance comparison of various combinations of generative models and representation basis spaces. We also propose a new evaluation metric which captures the deficiency of generating images in pixel space.

Ellipse Loss for Scene-Compliant Motion Prediction

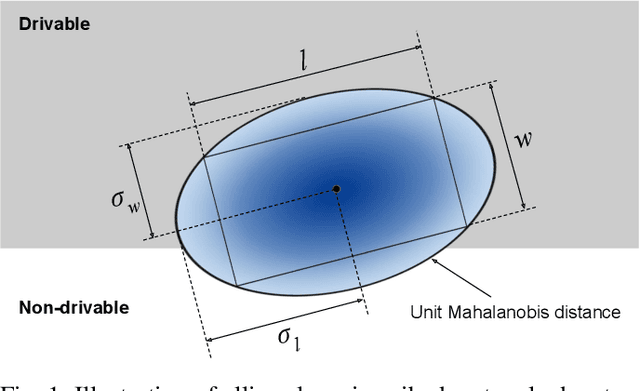
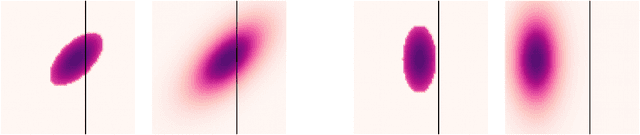
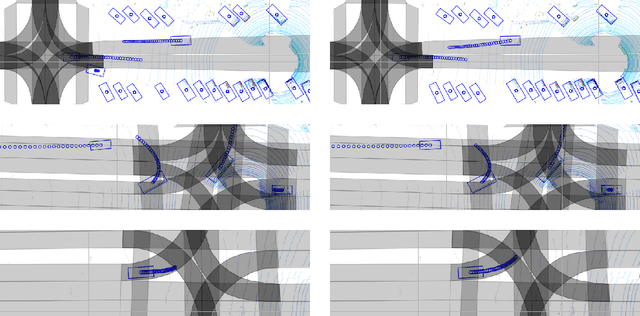
Motion prediction is a critical part of self-driving technology, responsible for inferring future behavior of traffic actors in autonomous vehicle's surroundings. In order to ensure safe and efficient operations, prediction models need to output accurate trajectories that obey the map constraints. In this paper, we address this task and propose a novel ellipse loss that allows the models to better reason about scene compliance and predict more realistic trajectories. Ellipse loss penalizes off-road predictions directly in a supervised manner, by projecting the output trajectories into the top-down map frame using a differentiable trajectory rasterizer module. Moreover, it takes into account the actor dimension and orientation, providing more direct training signals to the model. We applied ellipse loss to a recently proposed state-of-the-art joint detection-prediction model to showcase its benefits. Evaluation results on a large-scale autonomous driving data set strongly indicate that our method allows for more accurate and more realistic trajectory predictions.

A Unified Framework for Multiclass and Multilabel Support Vector Machines

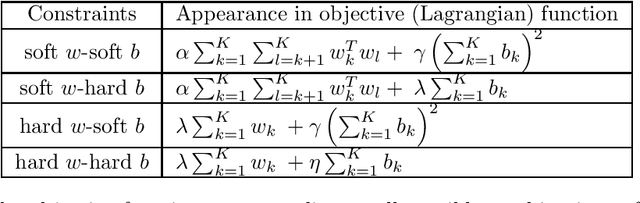
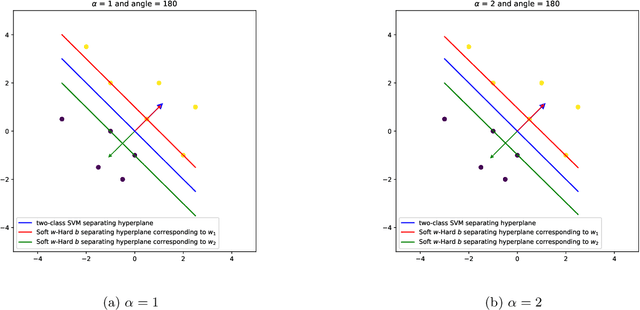
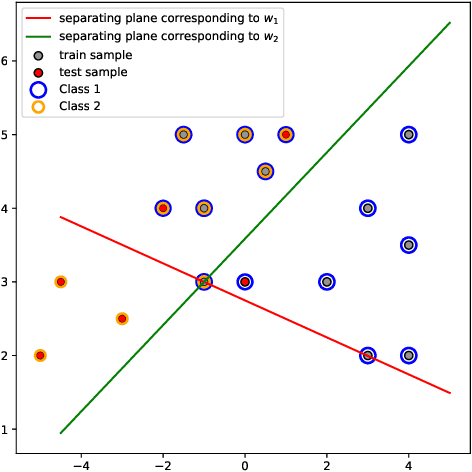
We propose a novel integrated formulation for multiclass and multilabel support vector machines (SVMs). A number of approaches have been proposed to extend the original binary SVM to an all-in-one multiclass SVM. However, its direct extension to a unified multilabel SVM has not been widely investigated. We propose a straightforward extension to the SVM to cope with multiclass and multilabel classification problems within a unified framework. Our framework deviates from the conventional soft margin SVM framework with its direct oppositional structure. In our formulation, class-specific weight vectors (normal vectors) are learned by maximizing their margin with respect to an origin and penalizing patterns when they get too close to this origin. As a result, each weight vector chooses an orientation and a magnitude with respect to this origin in such a way that it best represents the patterns belonging to its corresponding class. Opposition between classes is introduced into the formulation via the minimization of pairwise inner products of weight vectors. We also extend our framework to cope with nonlinear separability via standard reproducing kernel Hilbert spaces (RKHS). Biases which are closely related to the origin need to be treated properly in both the original feature space and Hilbert space. We have the flexibility to incorporate constraints into the formulation (if they better reflect the underlying geometry) and improve the performance of the classifier. To this end, specifics and technicalities such as the origin in RKHS are addressed. Results demonstrates a competitive classifier for both multiclass and multilabel classification problems.

A Hidden Variables Approach to Multilabel Logistic Regression

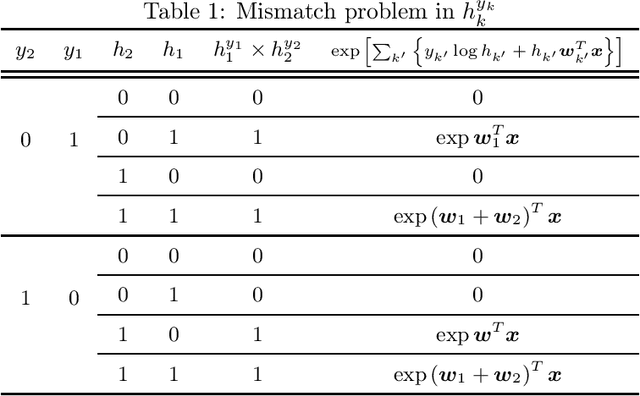
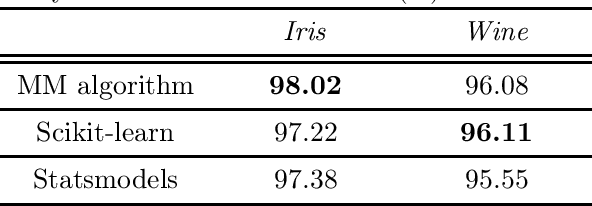
Multilabel classification is an important problem in a wide range of domains such as text categorization and music annotation. In this paper, we present a probabilistic model, Multilabel Logistic Regression with Hidden variables (MLRH), which extends the standard logistic regression by introducing hidden variables. Hidden variables make it possible to go beyond the conventional multiclass logistic regression by relaxing the one-hot-encoding constraint. We define a new joint distribution of labels and hidden variables which enables us to obtain one classifier for multilabel classification. Our experimental studies on a set of benchmark datasets demonstrate that the probabilistic model can achieve competitive performance compared with other multilabel learning algorithms.