Miroslav Stoyanov
Stable Anderson Acceleration for Deep Learning
Oct 26, 2021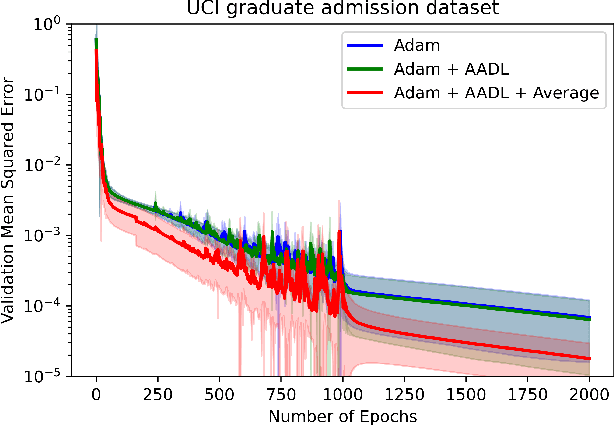
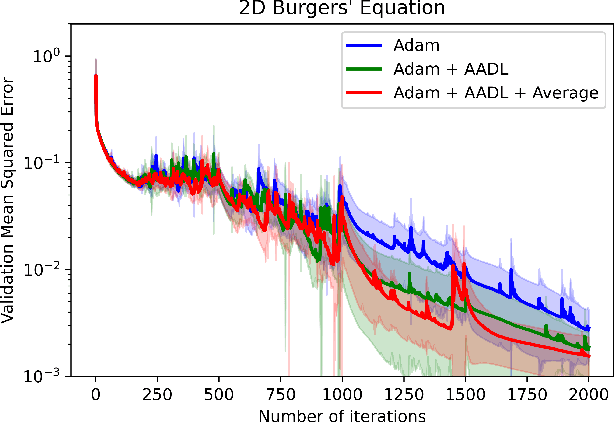
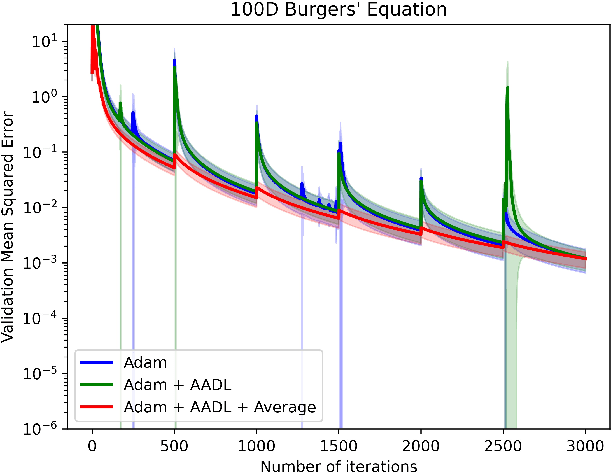
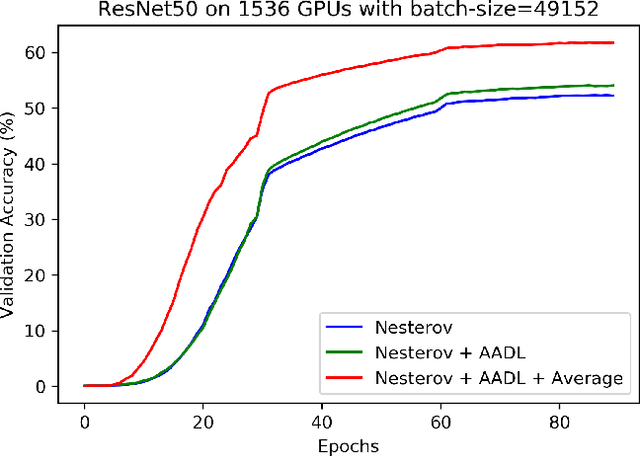
Abstract:Anderson acceleration (AA) is an extrapolation technique designed to speed-up fixed-point iterations like those arising from the iterative training of DL models. Training DL models requires large datasets processed in randomly sampled batches that tend to introduce in the fixed-point iteration stochastic oscillations of amplitude roughly inversely proportional to the size of the batch. These oscillations reduce and occasionally eliminate the positive effect of AA. To restore AA's advantage, we combine it with an adaptive moving average procedure that smoothes the oscillations and results in a more regular sequence of gradient descent updates. By monitoring the relative standard deviation between consecutive iterations, we also introduce a criterion to automatically assess whether the moving average is needed. We applied the method to the following DL instantiations: (i) multi-layer perceptrons (MLPs) trained on the open-source graduate admissions dataset for regression, (ii) physics informed neural networks (PINNs) trained on source data to solve 2d and 100d Burgers' partial differential equations (PDEs), and (iii) ResNet50 trained on the open-source ImageNet1k dataset for image classification. Numerical results obtained using up to 1,536 NVIDIA V100 GPUs on the OLCF supercomputer Summit showed the stabilizing effect of the moving average on AA for all the problems above.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge