Examining Policy Entropy of Reinforcement Learning Agents for Personalization Tasks

This effort is focused on examining the behavior of reinforcement learning systems in personalization environments and detailing the differences in policy entropy associated with the type of learning algorithm utilized. We demonstrate that Policy Optimization agents often possess low-entropy policies during training, which in practice results in agents prioritizing certain actions and avoiding others. Conversely, we also show that Q-Learning agents are far less susceptible to such behavior and generally maintain high-entropy policies throughout training, which is often preferable in real-world applications. We provide a wide range of numerical experiments as well as theoretical justification to show that these differences in entropy are due to the type of learning being employed.

An adaptive stochastic gradient-free approach for high-dimensional blackbox optimization

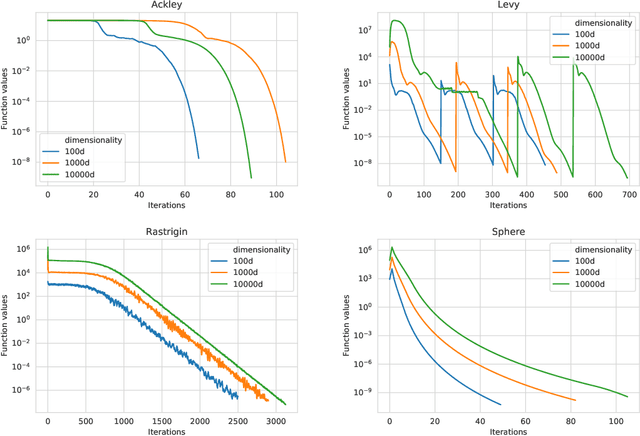
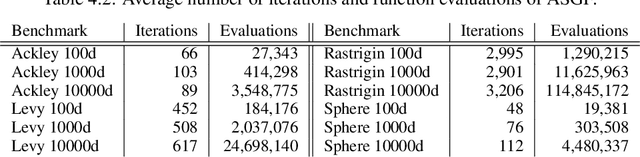
In this work, we propose a novel adaptive stochastic gradient-free (ASGF) approach for solving high-dimensional nonconvex optimization problems based on function evaluations. We employ a directional Gaussian smoothing of the target function that generates a surrogate of the gradient and assists in avoiding bad local optima by utilizing nonlocal information of the loss landscape. Applying a deterministic quadrature scheme results in a massively scalable technique that is sample-efficient and achieves spectral accuracy. At each step we randomly generate the search directions while primarily following the surrogate of the smoothed gradient. This enables exploitation of the gradient direction while maintaining sufficient space exploration, and accelerates convergence towards the global extrema. In addition, we make use of a local approximation of the Lipschitz constant in order to adaptively adjust the values of all hyperparameters, thus removing the careful fine-tuning of current algorithms that is often necessary to be successful when applied to a large class of learning tasks. As such, the ASGF strategy offers significant improvements when solving high-dimensional nonconvex optimization problems when compared to other gradient-free methods (including the so called "evolutionary strategies") as well as iterative approaches that rely on the gradient information of the objective function. We illustrate the improved performance of this method by providing several comparative numerical studies on benchmark global optimization problems and reinforcement learning tasks.

A nonlocal feature-driven exemplar-based approach for image inpainting

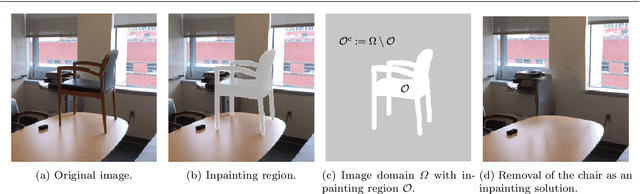
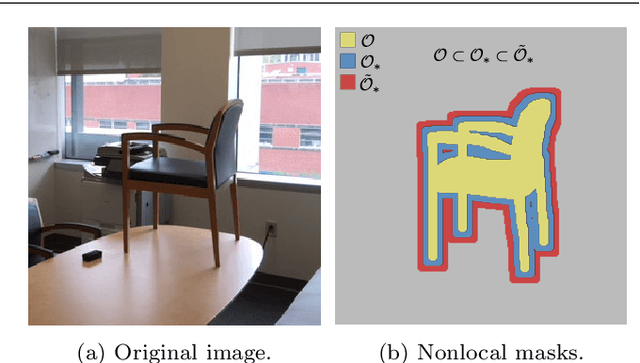
We present a nonlocal variational image completion technique which admits simultaneous inpainting of multiple structures and textures in a unified framework. The recovery of geometric structures is achieved by using general convolution operators as a measure of behavior within an image. These are combined with a nonlocal exemplar-based approach to exploit the self-similarity of an image in the selected feature domains and to ensure the inpainting of textures. We also introduce an anisotropic patch distance metric to allow for better control of the feature selection within an image and present a nonlocal energy functional based on this metric. Finally, we derive an optimization algorithm for the proposed variational model and examine its validity experimentally with various test images.

A Polynomial-Based Approach for Architectural Design and Learning with Deep Neural Networks

In this effort we propose a novel approach for reconstructing multivariate functions from training data, by identifying both a suitable network architecture and an initialization using polynomial-based approximations. Training deep neural networks using gradient descent can be interpreted as moving the set of network parameters along the loss landscape in order to minimize the loss functional. The initialization of parameters is important for iterative training methods based on descent. Our procedure produces a network whose initial state is a polynomial representation of the training data. The major advantage of this technique is from this initialized state the network may be improved using standard training procedures. Since the network already approximates the data, training is more likely to produce a set of parameters associated with a desirable local minimum. We provide the details of the theory necessary for constructing such networks and also consider several numerical examples that reveal our approach ultimately produces networks which can be effectively trained from our initialized state to achieve an improved approximation for a large class of target functions.