The Robots are Here: Navigating the Generative AI Revolution in Computing Education

Recent advancements in artificial intelligence (AI) are fundamentally reshaping computing, with large language models (LLMs) now effectively being able to generate and interpret source code and natural language instructions. These emergent capabilities have sparked urgent questions in the computing education community around how educators should adapt their pedagogy to address the challenges and to leverage the opportunities presented by this new technology. In this working group report, we undertake a comprehensive exploration of LLMs in the context of computing education and make five significant contributions. First, we provide a detailed review of the literature on LLMs in computing education and synthesise findings from 71 primary articles. Second, we report the findings of a survey of computing students and instructors from across 20 countries, capturing prevailing attitudes towards LLMs and their use in computing education contexts. Third, to understand how pedagogy is already changing, we offer insights collected from in-depth interviews with 22 computing educators from five continents who have already adapted their curricula and assessments. Fourth, we use the ACM Code of Ethics to frame a discussion of ethical issues raised by the use of large language models in computing education, and we provide concrete advice for policy makers, educators, and students. Finally, we benchmark the performance of LLMs on various computing education datasets, and highlight the extent to which the capabilities of current models are rapidly improving. Our aim is that this report will serve as a focal point for both researchers and practitioners who are exploring, adapting, using, and evaluating LLMs and LLM-based tools in computing classrooms.

Generative AI for Programming Education: Benchmarking ChatGPT, GPT-4, and Human Tutors

Generative AI and large language models hold great promise in enhancing computing education by powering next-generation educational technologies for introductory programming. Recent works have studied these models for different scenarios relevant to programming education; however, these works are limited for several reasons, as they typically consider already outdated models or only specific scenario(s). Consequently, there is a lack of a systematic study that benchmarks state-of-the-art models for a comprehensive set of programming education scenarios. In our work, we systematically evaluate two models, ChatGPT (based on GPT-3.5) and GPT-4, and compare their performance with human tutors for a variety of scenarios. We evaluate using five introductory Python programming problems and real-world buggy programs from an online platform, and assess performance using expert-based annotations. Our results show that GPT-4 drastically outperforms ChatGPT (based on GPT-3.5) and comes close to human tutors' performance for several scenarios. These results also highlight settings where GPT-4 still struggles, providing exciting future directions on developing techniques to improve the performance of these models.

LF-PPL: A Low-Level First Order Probabilistic Programming Language for Non-Differentiable Models

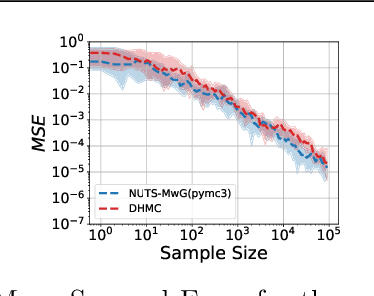
We develop a new Low-level, First-order Probabilistic Programming Language (LF-PPL) suited for models containing a mix of continuous, discrete, and/or piecewise-continuous variables. The key success of this language and its compilation scheme is in its ability to automatically distinguish parameters the density function is discontinuous with respect to, while further providing runtime checks for boundary crossings. This enables the introduction of new inference engines that are able to exploit gradient information, while remaining efficient for models which are not everywhere differentiable. We demonstrate this ability by incorporating a discontinuous Hamiltonian Monte Carlo (DHMC) inference engine that is able to deliver automated and efficient inference for non-differentiable models. Our system is backed up by a mathematical formalism that ensures that any model expressed in this language has a density with measure zero discontinuities to maintain the validity of the inference engine.

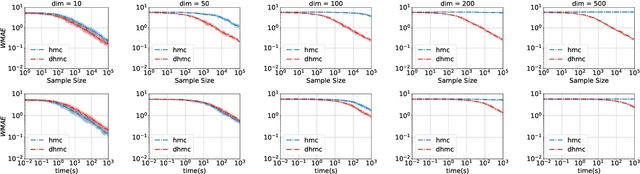
Discontinuous Hamiltonian Monte Carlo for Probabilistic Programs

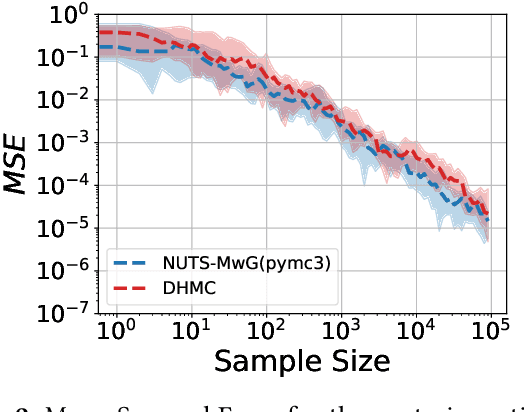
Hamiltonian Monte Carlo (HMC) is the dominant statistical inference algorithm used in most popular first-order differentiable probabilistic programming languages. HMC requires that the joint density be differentiable with respect to all latent variables. This complicates expressing some models in such languages and prohibits others. A recently proposed new integrator for HMC yielded a new Discontinuous HMC (DHMC) algorithm that can be used for inference in models with joint densities that have discontinuities. In this paper we show how to use DHMC for inference in probabilistic programs. To do this we introduce a sufficient set of language restrictions, a corresponding mathematical formalism that ensures that any joint density denoted in such a language has a suitably low measure of discontinuous points, and a recipe for how to apply DHMC in the more general probabilistic-programming context. Our experimental findings demonstrate the correctness of this approach.