Discontinuous Hamiltonian Monte Carlo for Probabilistic Programs

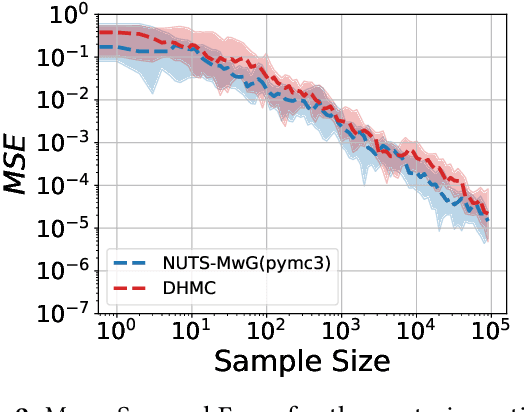
Hamiltonian Monte Carlo (HMC) is the dominant statistical inference algorithm used in most popular first-order differentiable probabilistic programming languages. HMC requires that the joint density be differentiable with respect to all latent variables. This complicates expressing some models in such languages and prohibits others. A recently proposed new integrator for HMC yielded a new Discontinuous HMC (DHMC) algorithm that can be used for inference in models with joint densities that have discontinuities. In this paper we show how to use DHMC for inference in probabilistic programs. To do this we introduce a sufficient set of language restrictions, a corresponding mathematical formalism that ensures that any joint density denoted in such a language has a suitably low measure of discontinuous points, and a recipe for how to apply DHMC in the more general probabilistic-programming context. Our experimental findings demonstrate the correctness of this approach.