Beyond Time: Cross-Dimensional Frequency Supervision for Time Series Forecasting

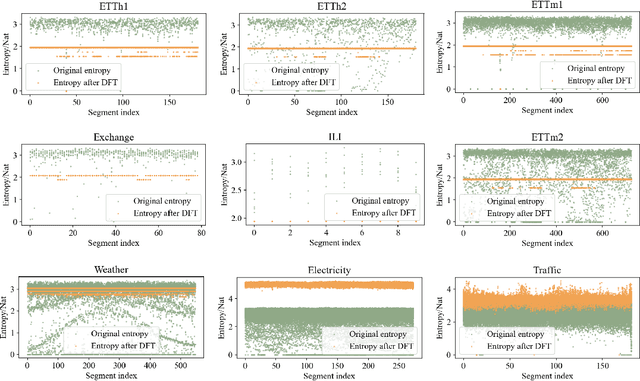
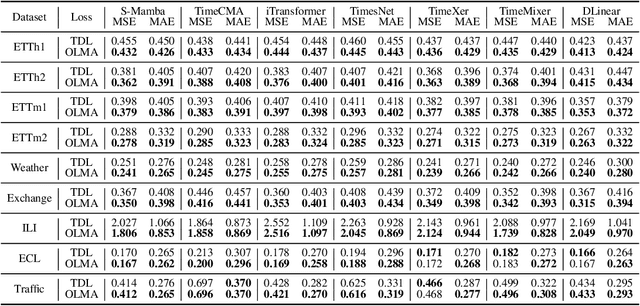
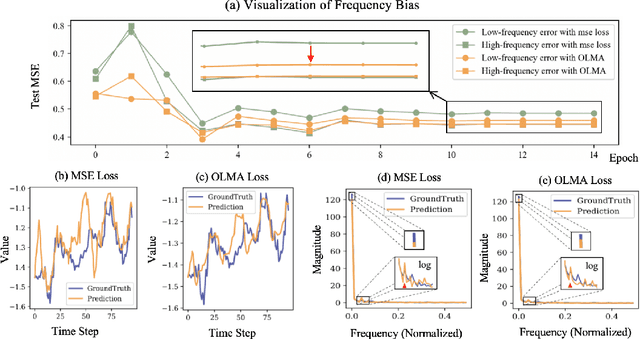
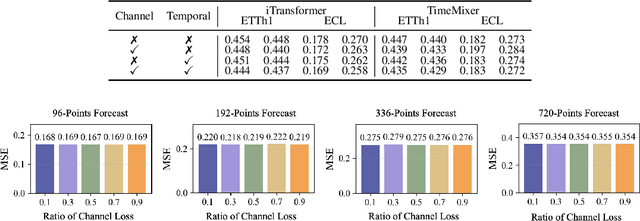
Time series forecasting plays a crucial role in various fields, and the methods based on frequency domain analysis have become an important branch. However, most existing studies focus on the design of elaborate model architectures and are often tailored for limited datasets, still lacking universality. Besides, the assumption of independent and identically distributed (IID) data also contradicts the strong correlation of the time domain labels. To address these issues, abandoning time domain supervision, we propose a purely frequency domain supervision approach named cross-dimensional frequency (X-Freq) loss. Specifically, based on a statistical phenomenon, we first prove that the information entropy of the time series is higher than its spectral entropy, which implies higher certainty in frequency domain and thus can provide better supervision. Secondly, the Fourier Transform and the Wavelet Transform are applied to the time dimension and the channel dimension of the time series respectively, to capture the long-term and short-term frequency variations as well as the spatial configuration features. Thirdly, the loss between predictions and targets is uniformly computed in the frequency domain. Moreover, we plug-and-play incorporate X-Freq into multiple advanced forecasting models and compare on 14 real-world datasets. The experimental results demonstrate that, without making any modification to the original architectures or hyperparameters, X-Freq can improve the forecasting performance by an average of 3.3% on long-term forecasting datasets and 27.7% on short-term ones, showcasing superior generality and practicality. The code will be released publicly.

Joint Task Offloading and Channel Allocation in Spatial-Temporal Dynamic for MEC Networks

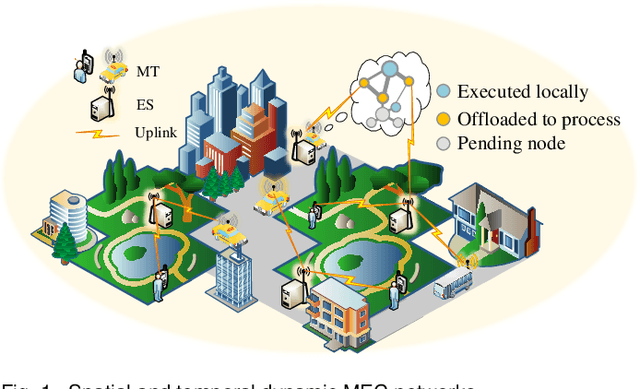
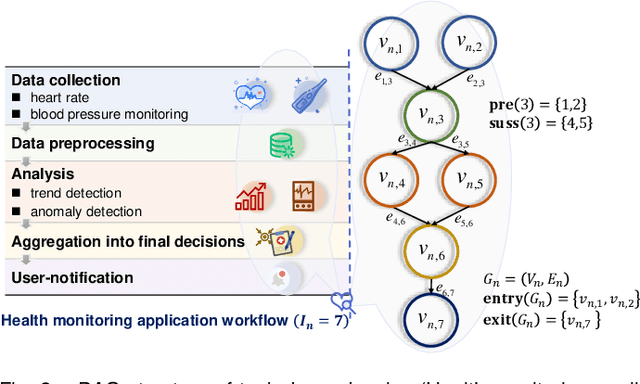
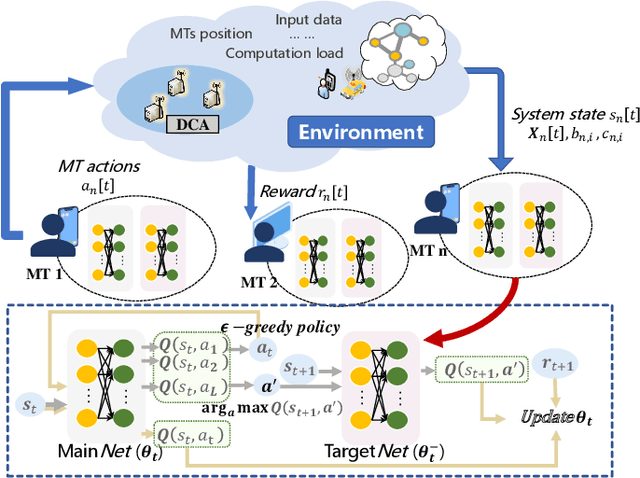
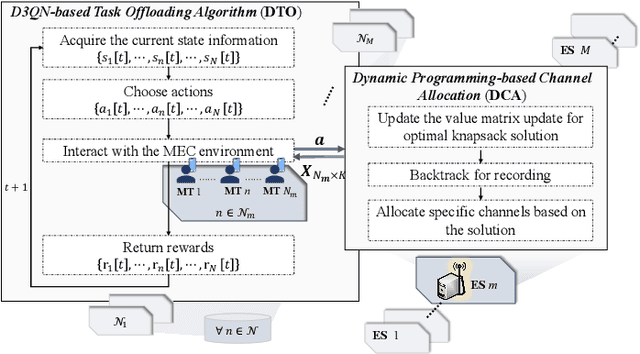
Computation offloading and resource allocation are critical in mobile edge computing (MEC) systems to handle the massive and complex requirements of applications restricted by limited resources. In a multi-user multi-server MEC network, the mobility of terminals causes computing requests to be dynamically distributed in space. At the same time, the non-negligible dependencies among tasks in some specific applications impose temporal correlation constraints on the solution as well, leading the time-adjacent tasks to experience varying resource availability and competition from parallel counterparts. To address such dynamic spatial-temporal characteristics as a challenge in the allocation of communication and computation resources, we formulate a long-term delay-energy trade-off cost minimization problem in the view of jointly optimizing task offloading and resource allocation. We begin by designing a priority evaluation scheme to decouple task dependencies and then develop a grouped Knapsack problem for channel allocation considering the current data load and channel status. Afterward, in order to meet the rapid response needs of MEC systems, we exploit the double duel deep Q network (D3QN) to make offloading decisions and integrate channel allocation results into the reward as part of the dynamic environment feedback in D3QN, constituting the joint optimization of task offloading and channel allocation. Finally, comprehensive simulations demonstrate the performance of the proposed algorithm in the delay-energy trade-off cost and its adaptability for various applications.

FreeCOS: Self-Supervised Learning from Fractals and Unlabeled Images for Curvilinear Object Segmentation

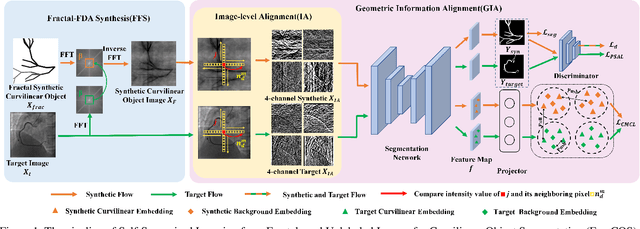
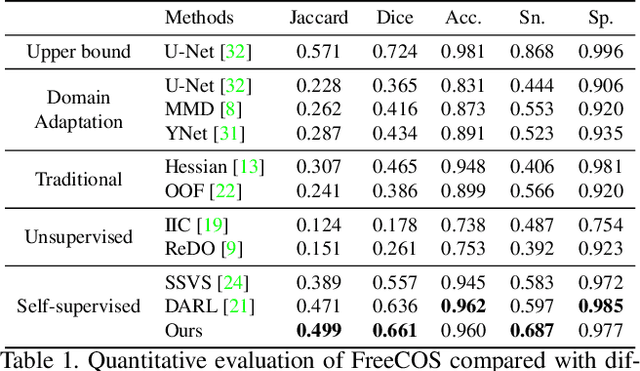
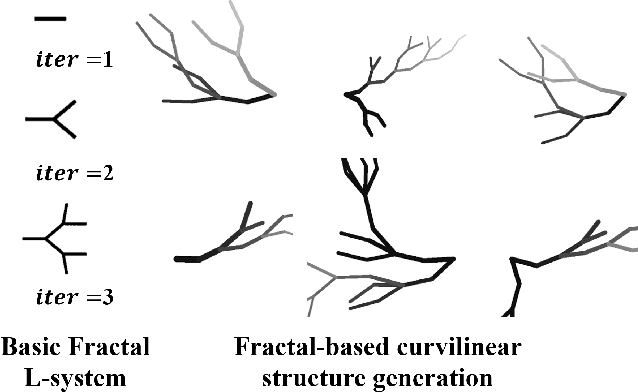
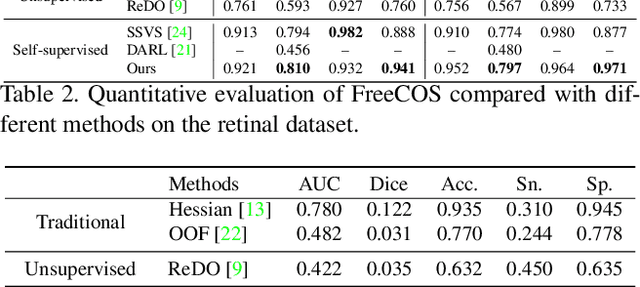
Curvilinear object segmentation is critical for many applications. However, manually annotating curvilinear objects is very time-consuming and error-prone, yielding insufficiently available annotated datasets for existing supervised methods and domain adaptation methods. This paper proposes a self-supervised curvilinear object segmentation method that learns robust and distinctive features from fractals and unlabeled images (FreeCOS). The key contributions include a novel Fractal-FDA synthesis (FFS) module and a geometric information alignment (GIA) approach. FFS generates curvilinear structures based on the parametric Fractal L-system and integrates the generated structures into unlabeled images to obtain synthetic training images via Fourier Domain Adaptation. GIA reduces the intensity differences between the synthetic and unlabeled images by comparing the intensity order of a given pixel to the values of its nearby neighbors. Such image alignment can explicitly remove the dependency on absolute intensity values and enhance the inherent geometric characteristics which are common in both synthetic and real images. In addition, GIA aligns features of synthetic and real images via the prediction space adaptation loss (PSAL) and the curvilinear mask contrastive loss (CMCL). Extensive experimental results on four public datasets, i.e., XCAD, DRIVE, STARE and CrackTree demonstrate that our method outperforms the state-of-the-art unsupervised methods, self-supervised methods and traditional methods by a large margin. The source code of this work is available at https://github.com/TY-Shi/FreeCOS.

Affinity Feature Strengthening for Accurate, Complete and Robust Vessel Segmentation

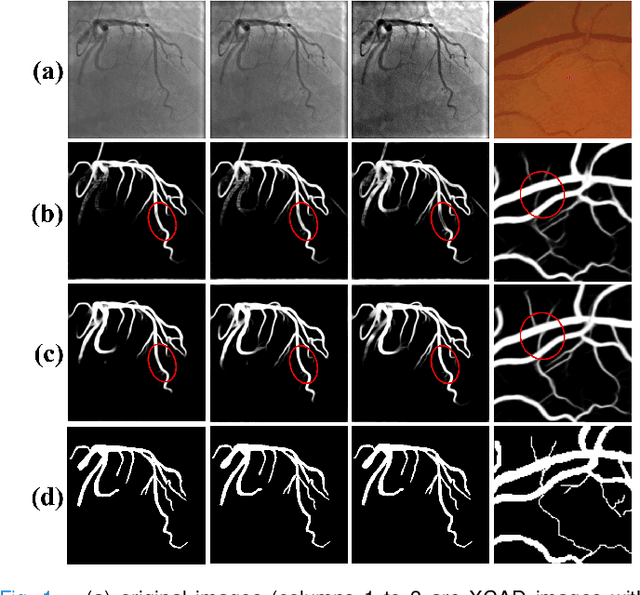
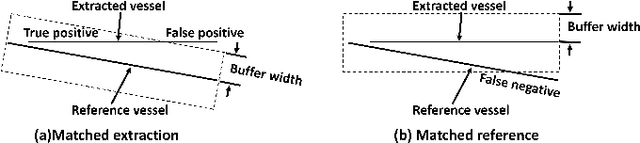
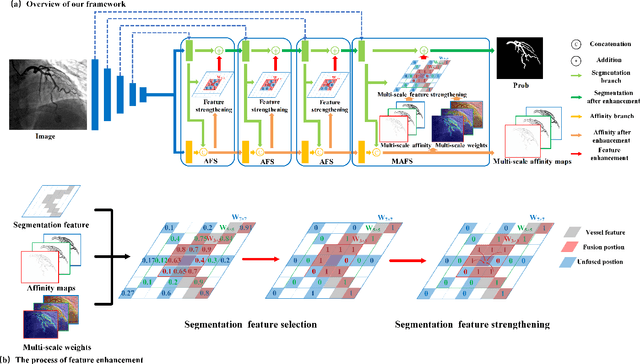
Vessel segmentation is essential in many medical image applications, such as the detection of coronary stenoses, retinal vessel diseases and brain aneurysms. A high pixel-wise accuracy, complete topology structure and robustness to various contrast variations are three critical aspects of vessel segmentation. However, most existing methods only focus on achieving part of them via dedicated designs while few of them can concurrently achieve the three goals. In this paper, we present a novel affinity feature strengthening network (AFN) which adopts a contrast-insensitive approach based on multiscale affinity to jointly model topology and refine pixel-wise segmentation features. Specifically, for each pixel we derive a multiscale affinity field which captures the semantic relationships of the pixel with its neighbors on the predicted mask image. Such a multiscale affinity field can effectively represent the local topology of a vessel segment of different sizes. Meanwhile, it does not depend on image intensities and hence is robust to various illumination and contrast changes. We further learn spatial- and scale-aware adaptive weights for the corresponding affinity fields to strengthen vessel features. We evaluate our AFN on four different types of vascular datasets: X-ray angiography coronary vessel dataset (XCAD), portal vein dataset (PV), digital subtraction angiography cerebrovascular vessel dataset (DSA) and retinal vessel dataset (DRIVE). Extensive experimental results on the four datasets demonstrate that our AFN outperforms the state-of-the-art methods in terms of both higher accuracy and topological metrics, and meanwhile is more robust to various contrast changes than existing methods. Codes will be made public.

Learning Green's functions associated with parabolic partial differential equations

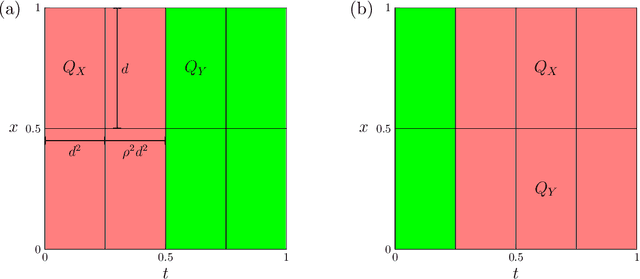
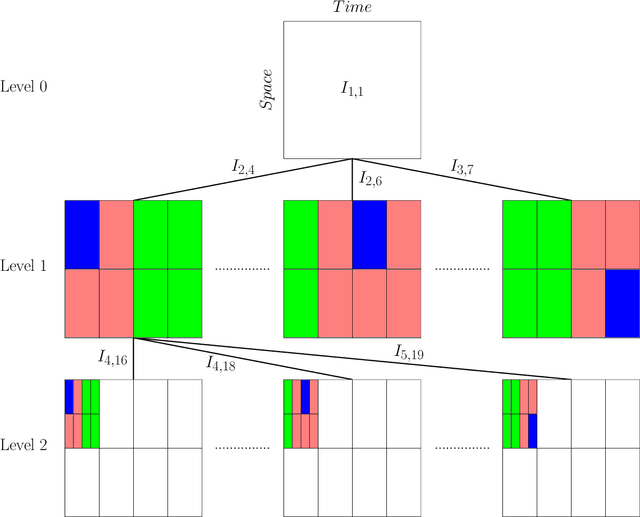
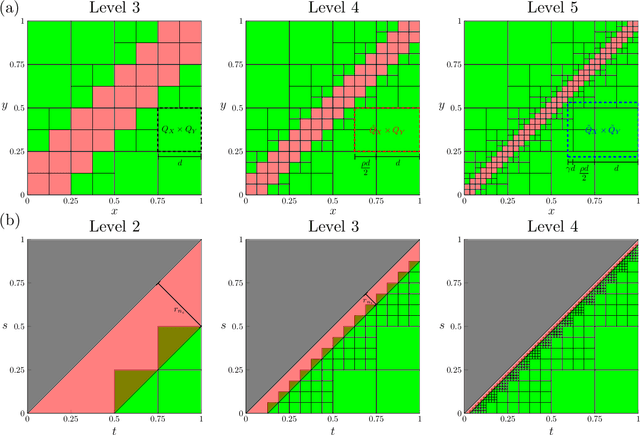
Given input-output pairs from a parabolic partial differential equation (PDE) in any spatial dimension $n\geq 1$, we derive the first theoretically rigorous scheme for learning the associated Green's function $G$. Until now, rigorously learning Green's functions associated with parabolic operators has been a major challenge in the field of scientific machine learning because $G$ may not be square-integrable when $n>1$, and time-dependent PDEs have transient dynamics. By combining the hierarchical low-rank structure of $G$ together with the randomized singular value decomposition, we construct an approximant to $G$ that achieves a relative error of $\smash{\mathcal{O}(\Gamma_\epsilon^{-1/2}\epsilon)}$ in the $L^1$-norm with high probability by using at most $\smash{\mathcal{O}(\epsilon^{-\frac{n+2}{2}}\log(1/\epsilon))}$ input-output training pairs, where $\Gamma_\epsilon$ is a measure of the quality of the training dataset for learning $G$, and $\epsilon>0$ is sufficiently small. Along the way, we extend the low-rank theory of Bebendorf and Hackbusch from elliptic PDEs in dimension $1\leq n\leq 3$ to parabolic PDEs in any dimensions, which shows that Green's functions associated with parabolic PDEs admit a low-rank structure on well-separated domains.

Local Intensity Order Transformation for Robust Curvilinear Object Segmentation

Segmentation of curvilinear structures is important in many applications, such as retinal blood vessel segmentation for early detection of vessel diseases and pavement crack segmentation for road condition evaluation and maintenance. Currently, deep learning-based methods have achieved impressive performance on these tasks. Yet, most of them mainly focus on finding powerful deep architectures but ignore capturing the inherent curvilinear structure feature (e.g., the curvilinear structure is darker than the context) for a more robust representation. In consequence, the performance usually drops a lot on cross-datasets, which poses great challenges in practice. In this paper, we aim to improve the generalizability by introducing a novel local intensity order transformation (LIOT). Specifically, we transfer a gray-scale image into a contrast-invariant four-channel image based on the intensity order between each pixel and its nearby pixels along with the four (horizontal and vertical) directions. This results in a representation that preserves the inherent characteristic of the curvilinear structure while being robust to contrast changes. Cross-dataset evaluation on three retinal blood vessel segmentation datasets demonstrates that LIOT improves the generalizability of some state-of-the-art methods. Additionally, the cross-dataset evaluation between retinal blood vessel segmentation and pavement crack segmentation shows that LIOT is able to preserve the inherent characteristic of curvilinear structure with large appearance gaps. An implementation of the proposed method is available at https://github.com/TY-Shi/LIOT.