Learning Green's functions associated with parabolic partial differential equations
Paper and Code
Apr 27, 2022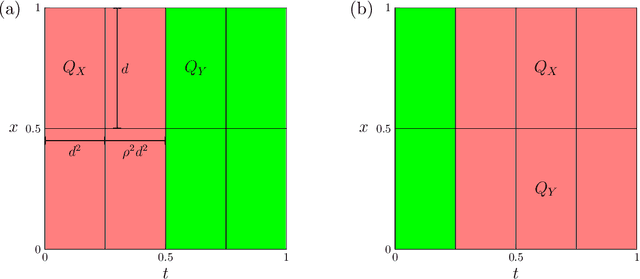
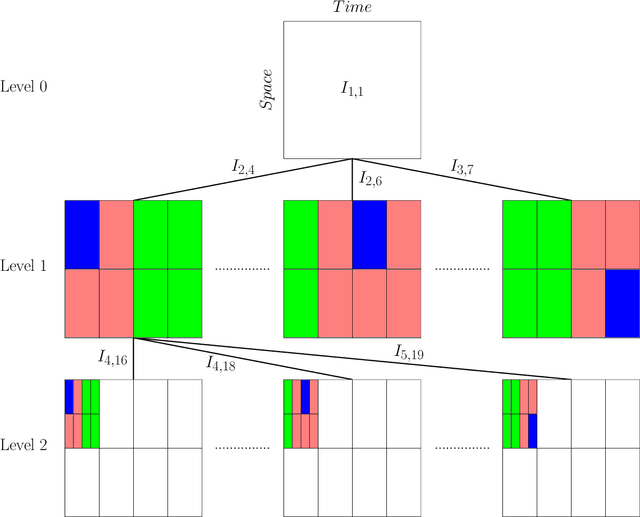
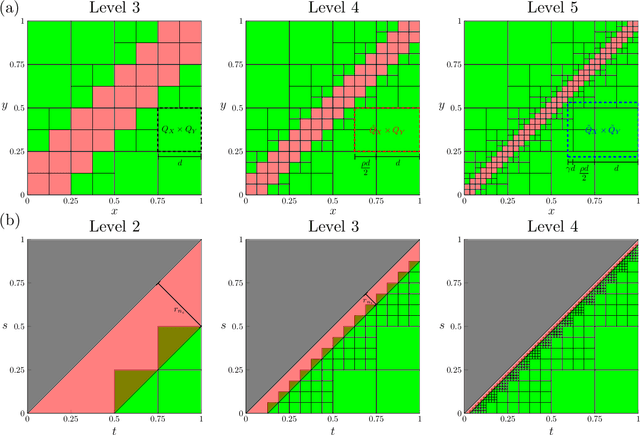
Given input-output pairs from a parabolic partial differential equation (PDE) in any spatial dimension $n\geq 1$, we derive the first theoretically rigorous scheme for learning the associated Green's function $G$. Until now, rigorously learning Green's functions associated with parabolic operators has been a major challenge in the field of scientific machine learning because $G$ may not be square-integrable when $n>1$, and time-dependent PDEs have transient dynamics. By combining the hierarchical low-rank structure of $G$ together with the randomized singular value decomposition, we construct an approximant to $G$ that achieves a relative error of $\smash{\mathcal{O}(\Gamma_\epsilon^{-1/2}\epsilon)}$ in the $L^1$-norm with high probability by using at most $\smash{\mathcal{O}(\epsilon^{-\frac{n+2}{2}}\log(1/\epsilon))}$ input-output training pairs, where $\Gamma_\epsilon$ is a measure of the quality of the training dataset for learning $G$, and $\epsilon>0$ is sufficiently small. Along the way, we extend the low-rank theory of Bebendorf and Hackbusch from elliptic PDEs in dimension $1\leq n\leq 3$ to parabolic PDEs in any dimensions, which shows that Green's functions associated with parabolic PDEs admit a low-rank structure on well-separated domains.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge