Pathological Prior-Guided Multiple Instance Learning For Mitigating Catastrophic Forgetting in Breast Cancer Whole Slide Image Classification

In histopathology, intelligent diagnosis of Whole Slide Images (WSIs) is essential for automating and objectifying diagnoses, reducing the workload of pathologists. However, diagnostic models often face the challenge of forgetting previously learned data during incremental training on datasets from different sources. To address this issue, we propose a new framework PaGMIL to mitigate catastrophic forgetting in breast cancer WSI classification. Our framework introduces two key components into the common MIL model architecture. First, it leverages microscopic pathological prior to select more accurate and diverse representative patches for MIL. Secondly, it trains separate classification heads for each task and uses macroscopic pathological prior knowledge, treating the thumbnail as a prompt guide (PG) to select the appropriate classification head. We evaluate the continual learning performance of PaGMIL across several public breast cancer datasets. PaGMIL achieves a better balance between the performance of the current task and the retention of previous tasks, outperforming other continual learning methods. Our code will be open-sourced upon acceptance.

Weakly Supervised Training for Hologram Verification in Identity Documents

We propose a method to remotely verify the authenticity of Optically Variable Devices (OVDs), often referred to as ``holograms'', in identity documents. Our method processes video clips captured with smartphones under common lighting conditions, and is evaluated on two public datasets: MIDV-HOLO and MIDV-2020. Thanks to a weakly-supervised training, we optimize a feature extraction and decision pipeline which achieves a new leading performance on MIDV-HOLO, while maintaining a high recall on documents from MIDV-2020 used as attack samples. It is also the first method, to date, to effectively address the photo replacement attack task, and can be trained on either genuine samples, attack samples, or both for increased performance. By enabling to verify OVD shapes and dynamics with very little supervision, this work opens the way towards the use of massive amounts of unlabeled data to build robust remote identity document verification systems on commodity smartphones. Code is available at https://github.com/EPITAResearchLab/pouliquen.24.icdar

Some equivalence relation between persistent homology and morphological dynamics

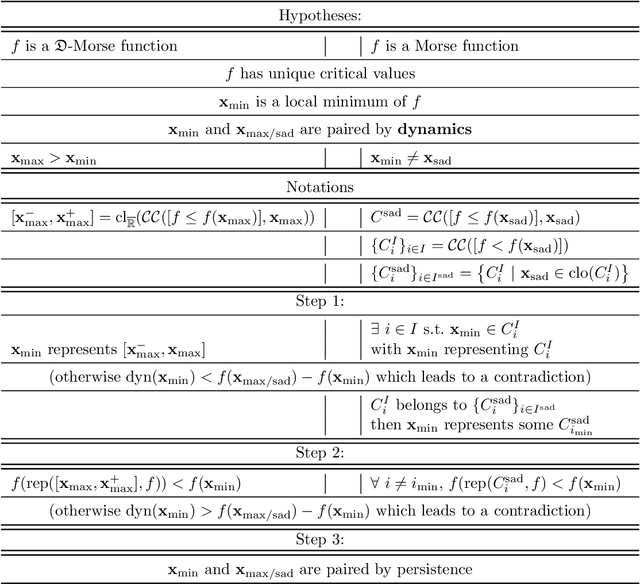
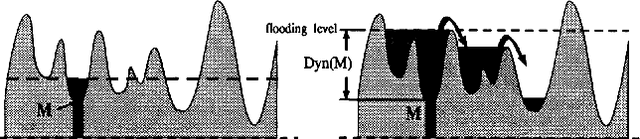
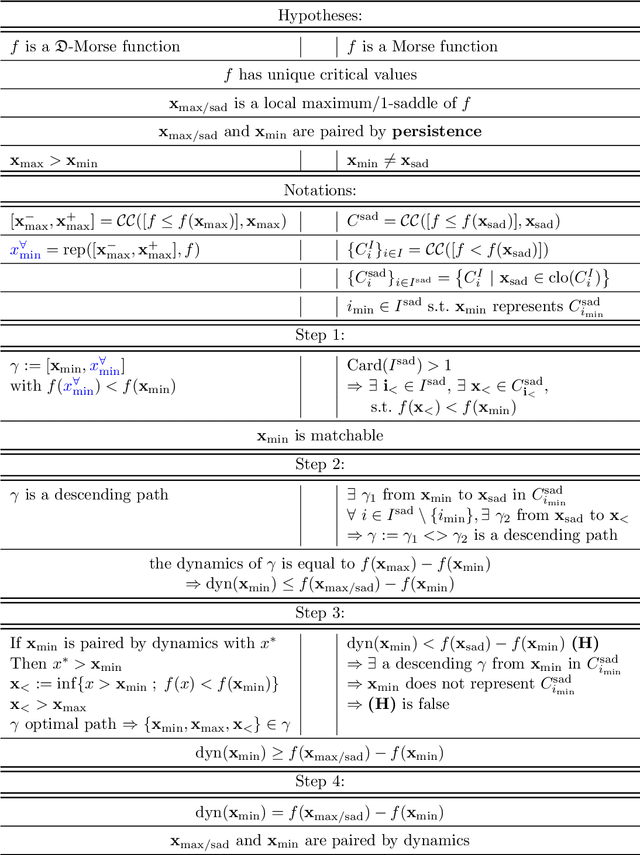
In Mathematical Morphology (MM), connected filters based on dynamics are used to filter the extrema of an image. Similarly, persistence is a concept coming from Persistent Homology (PH) and Morse Theory (MT) that represents the stability of the extrema of a Morse function. Since these two concepts seem to be closely related, in this paper we examine their relationship, and we prove that they are equal on n-D Morse functions, n $\ge$ 1. More exactly, pairing a minimum with a 1-saddle by dynamics or pairing the same 1-saddle with a minimum by persistence leads exactly to the same pairing, assuming that the critical values of the studied Morse function are unique. This result is a step further to show how much topological data analysis and mathematical morphology are related, paving the way for a more in-depth study of the relations between these two research fields.

Local Intensity Order Transformation for Robust Curvilinear Object Segmentation

Segmentation of curvilinear structures is important in many applications, such as retinal blood vessel segmentation for early detection of vessel diseases and pavement crack segmentation for road condition evaluation and maintenance. Currently, deep learning-based methods have achieved impressive performance on these tasks. Yet, most of them mainly focus on finding powerful deep architectures but ignore capturing the inherent curvilinear structure feature (e.g., the curvilinear structure is darker than the context) for a more robust representation. In consequence, the performance usually drops a lot on cross-datasets, which poses great challenges in practice. In this paper, we aim to improve the generalizability by introducing a novel local intensity order transformation (LIOT). Specifically, we transfer a gray-scale image into a contrast-invariant four-channel image based on the intensity order between each pixel and its nearby pixels along with the four (horizontal and vertical) directions. This results in a representation that preserves the inherent characteristic of the curvilinear structure while being robust to contrast changes. Cross-dataset evaluation on three retinal blood vessel segmentation datasets demonstrates that LIOT improves the generalizability of some state-of-the-art methods. Additionally, the cross-dataset evaluation between retinal blood vessel segmentation and pavement crack segmentation shows that LIOT is able to preserve the inherent characteristic of curvilinear structure with large appearance gaps. An implementation of the proposed method is available at https://github.com/TY-Shi/LIOT.

ICDAR 2021 Competition on Historical Map Segmentation

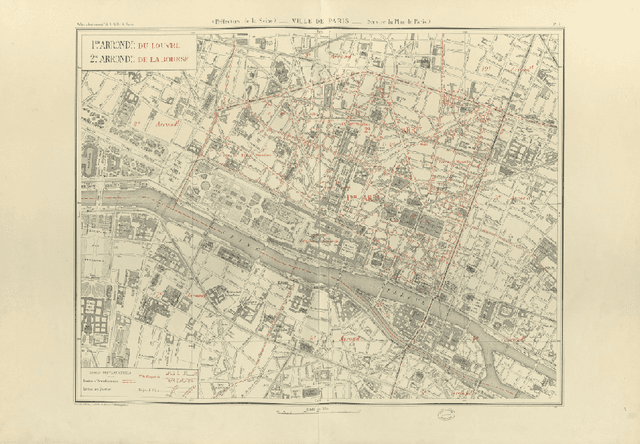
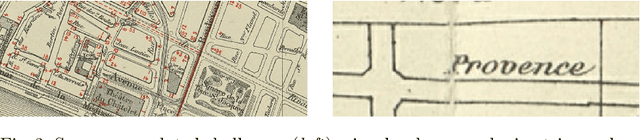
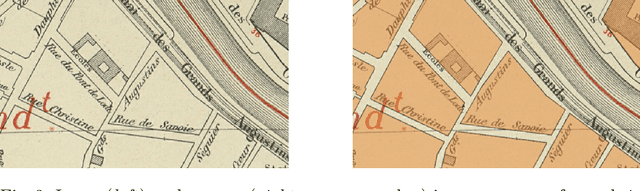
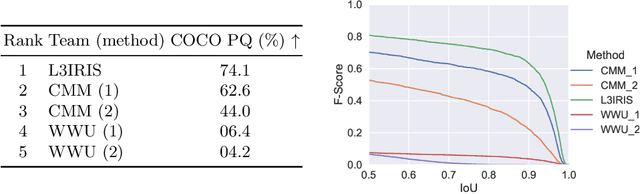
This paper presents the final results of the ICDAR 2021 Competition on Historical Map Segmentation (MapSeg), encouraging research on a series of historical atlases of Paris, France, drawn at 1/5000 scale between 1894 and 1937. The competition featured three tasks, awarded separately. Task~1 consists in detecting building blocks and was won by the L3IRIS team using a DenseNet-121 network trained in a weakly supervised fashion. This task is evaluated on 3 large images containing hundreds of shapes to detect. Task~2 consists in segmenting map content from the larger map sheet, and was won by the UWB team using a U-Net-like FCN combined with a binarization method to increase detection edge accuracy. Task~3 consists in locating intersection points of geo-referencing lines, and was also won by the UWB team who used a dedicated pipeline combining binarization, line detection with Hough transform, candidate filtering, and template matching for intersection refinement. Tasks~2 and~3 are evaluated on 95 map sheets with complex content. Dataset, evaluation tools and results are available under permissive licensing at \url{https://icdar21-mapseg.github.io/}.

Hierarchical image simplification and segmentation based on Mumford-Shah-salient level line selection

Hierarchies, such as the tree of shapes, are popular representations for image simplification and segmentation thanks to their multiscale structures. Selecting meaningful level lines (boundaries of shapes) yields to simplify image while preserving intact salient structures. Many image simplification and segmentation methods are driven by the optimization of an energy functional, for instance the celebrated Mumford-Shah functional. In this paper, we propose an efficient approach to hierarchical image simplification and segmentation based on the minimization of the piecewise-constant Mumford-Shah functional. This method conforms to the current trend that consists in producing hierarchical results rather than a unique partition. Contrary to classical approaches which compute optimal hierarchical segmentations from an input hierarchy of segmentations, we rely on the tree of shapes, a unique and well-defined representation equivalent to the image. Simply put, we compute for each level line of the image an attribute function that characterizes its persistence under the energy minimization. Then we stack the level lines from meaningless ones to salient ones through a saliency map based on extinction values defined on the tree-based shape space. Qualitative illustrations and quantitative evaluation on Weizmann segmentation evaluation database demonstrate the state-of-the-art performance of our method.

A fair comparison of many max-tree computation algorithms (Extended version of the paper submitted to ISMM 2013

With the development of connected filters for the last decade, many algorithms have been proposed to compute the max-tree. Max-tree allows to compute the most advanced connected operators in a simple way. However, no fair comparison of algorithms has been proposed yet and the choice of an algorithm over an other depends on many parameters. Since the need of fast algorithms is obvious for production code, we present an in depth comparison of five algorithms and some variations of them in a unique framework. Finally, a decision tree will be proposed to help user in choosing the right algorithm with respect to their data.

Writing Reusable Digital Geometry Algorithms in a Generic Image Processing Framework

Digital Geometry software should reflect the generality of the underlying mathe- matics: mapping the latter to the former requires genericity. By designing generic solutions, one can effectively reuse digital geometry data structures and algorithms. We propose an image processing framework focused on the Generic Programming paradigm in which an algorithm on the paper can be turned into a single code, written once and usable with various input types. This approach enables users to design and implement new methods at a lower cost, try cross-domain experiments and help generalize results

Morphological Filtering in Shape Spaces: Applications using Tree-Based Image Representations

Connected operators are filtering tools that act by merging elementary regions of an image. A popular strategy is based on tree-based image representations: for example, one can compute an attribute on each node of the tree and keep only the nodes for which the attribute is sufficiently strong. This operation can be seen as a thresholding of the tree, seen as a graph whose nodes are weighted by the attribute. Rather than being satisfied with a mere thresholding, we propose to expand on this idea, and to apply connected filters on this latest graph. Consequently, the filtering is done not in the space of the image, but on the space of shapes build from the image. Such a processing is a generalization of the existing tree-based connected operators. Indeed, the framework includes classical existing connected operators by attributes. It also allows us to propose a class of novel connected operators from the leveling family, based on shape attributes. Finally, we also propose a novel class of self-dual connected operators that we call morphological shapings.