Some equivalence relation between persistent homology and morphological dynamics
Paper and Code
May 25, 2022
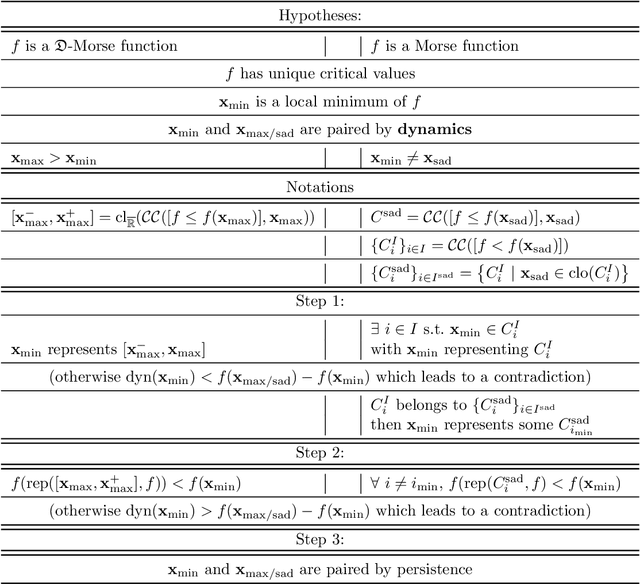
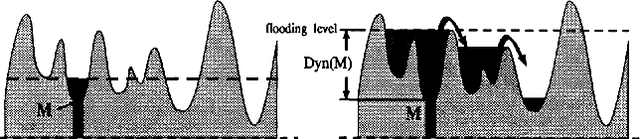
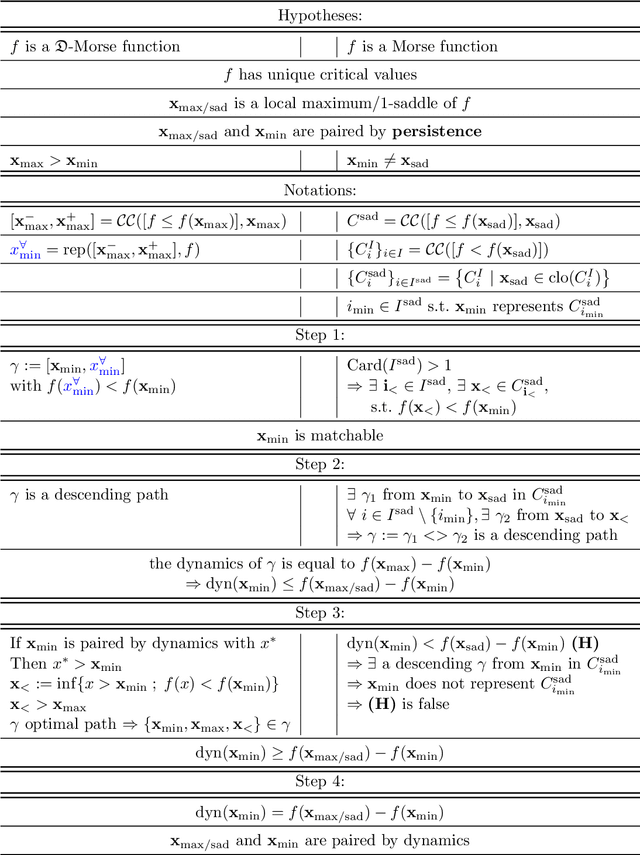
In Mathematical Morphology (MM), connected filters based on dynamics are used to filter the extrema of an image. Similarly, persistence is a concept coming from Persistent Homology (PH) and Morse Theory (MT) that represents the stability of the extrema of a Morse function. Since these two concepts seem to be closely related, in this paper we examine their relationship, and we prove that they are equal on n-D Morse functions, n $\ge$ 1. More exactly, pairing a minimum with a 1-saddle by dynamics or pairing the same 1-saddle with a minimum by persistence leads exactly to the same pairing, assuming that the critical values of the studied Morse function are unique. This result is a step further to show how much topological data analysis and mathematical morphology are related, paving the way for a more in-depth study of the relations between these two research fields.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge