Thomas O'Leary-Roseberry
Derivative-Informed Fourier Neural Operator: Universal Approximation and Applications to PDE-Constrained Optimization
Dec 16, 2025

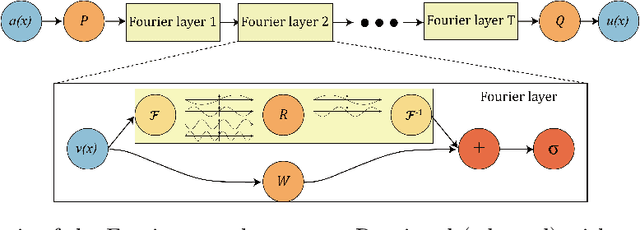
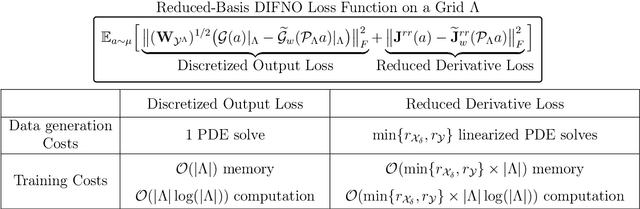
Abstract:We present approximation theories and efficient training methods for derivative-informed Fourier neural operators (DIFNOs) with applications to PDE-constrained optimization. A DIFNO is an FNO trained by minimizing its prediction error jointly on output and Fréchet derivative samples of a high-fidelity operator (e.g., a parametric PDE solution operator). As a result, a DIFNO can closely emulate not only the high-fidelity operator's response but also its sensitivities. To motivate the use of DIFNOs instead of conventional FNOs as surrogate models, we show that accurate surrogate-driven PDE-constrained optimization requires accurate surrogate Fréchet derivatives. Then, for continuously differentiable operators, we establish (i) simultaneous universal approximation of FNOs and their Fréchet derivatives on compact sets, and (ii) universal approximation of FNOs in weighted Sobolev spaces with input measures that have unbounded supports. Our theoretical results certify the capability of FNOs for accurate derivative-informed operator learning and accurate solution of PDE-constrained optimization. Furthermore, we develop efficient training schemes using dimension reduction and multi-resolution techniques that significantly reduce memory and computational costs for Fréchet derivative learning. Numerical examples on nonlinear diffusion--reaction, Helmholtz, and Navier--Stokes equations demonstrate that DIFNOs are superior in sample complexity for operator learning and solving infinite-dimensional PDE-constrained inverse problems, achieving high accuracy at low training sample sizes.
Dimension reduction for derivative-informed operator learning: An analysis of approximation errors
Apr 11, 2025Abstract:We study the derivative-informed learning of nonlinear operators between infinite-dimensional separable Hilbert spaces by neural networks. Such operators can arise from the solution of partial differential equations (PDEs), and are used in many simulation-based outer-loop tasks in science and engineering, such as PDE-constrained optimization, Bayesian inverse problems, and optimal experimental design. In these settings, the neural network approximations can be used as surrogate models to accelerate the solution of the outer-loop tasks. However, since outer-loop tasks in infinite dimensions often require knowledge of the underlying geometry, the approximation accuracy of the operator's derivatives can also significantly impact the performance of the surrogate model. Motivated by this, we analyze the approximation errors of neural operators in Sobolev norms over infinite-dimensional Gaussian input measures. We focus on the reduced basis neural operator (RBNO), which uses linear encoders and decoders defined on dominant input/output subspaces spanned by reduced sets of orthonormal bases. To this end, we study two methods for generating the bases; principal component analysis (PCA) and derivative-informed subspaces (DIS), which use the dominant eigenvectors of the covariance of the data or the derivatives as the reduced bases, respectively. We then derive bounds for errors arising from both the dimension reduction and the latent neural network approximation, including the sampling errors associated with the empirical estimation of the PCA/DIS. Our analysis is validated on numerical experiments with elliptic PDEs, where our results show that bases informed by the map (i.e., DIS or output PCA) yield accurate reconstructions and generalization errors for both the operator and its derivatives, while input PCA may underperform unless ranks and training sample sizes are sufficiently large.
Verification and Validation for Trustworthy Scientific Machine Learning
Feb 21, 2025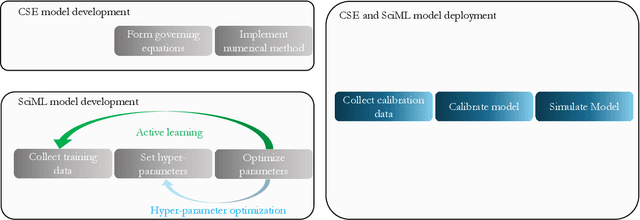
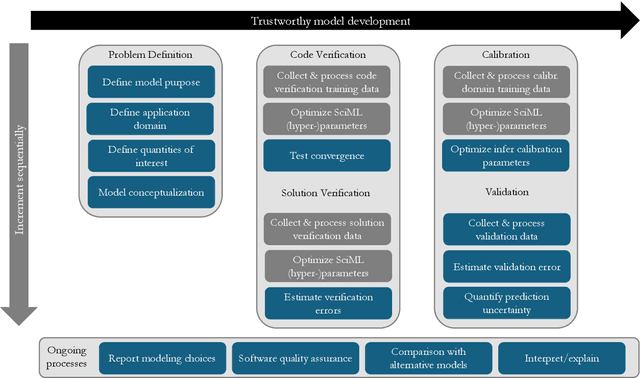
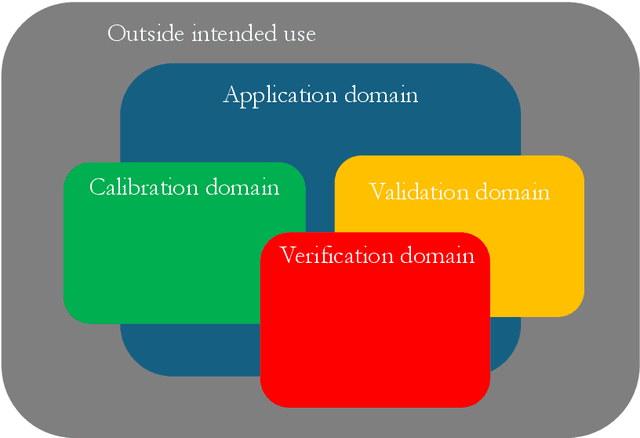
Abstract:Scientific machine learning (SciML) models are transforming many scientific disciplines. However, the development of good modeling practices to increase the trustworthiness of SciML has lagged behind its application, limiting its potential impact. The goal of this paper is to start a discussion on establishing consensus-based good practices for predictive SciML. We identify key challenges in applying existing computational science and engineering guidelines, such as verification and validation protocols, and provide recommendations to address these challenges. Our discussion focuses on predictive SciML, which uses machine learning models to learn, improve, and accelerate numerical simulations of physical systems. While centered on predictive applications, our 16 recommendations aim to help researchers conduc
LazyDINO: Fast, scalable, and efficiently amortized Bayesian inversion via structure-exploiting and surrogate-driven measure transport
Nov 19, 2024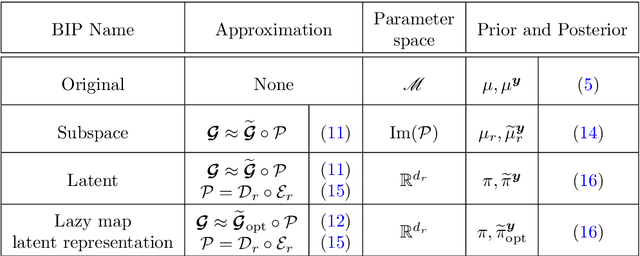
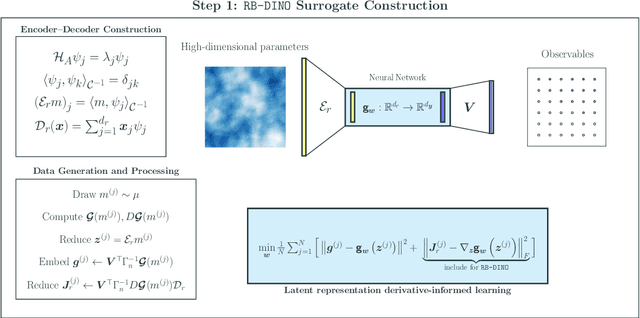
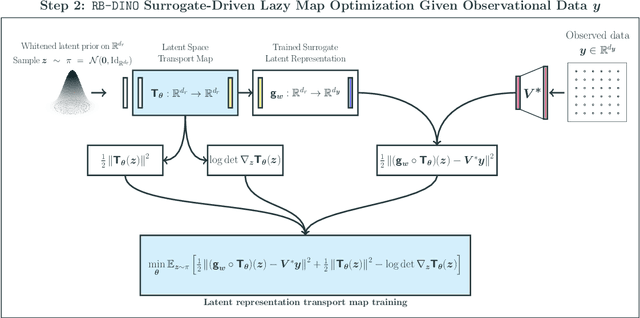
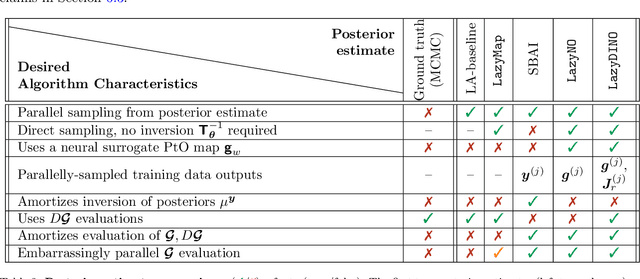
Abstract:We present LazyDINO, a transport map variational inference method for fast, scalable, and efficiently amortized solutions of high-dimensional nonlinear Bayesian inverse problems with expensive parameter-to-observable (PtO) maps. Our method consists of an offline phase in which we construct a derivative-informed neural surrogate of the PtO map using joint samples of the PtO map and its Jacobian. During the online phase, when given observational data, we seek rapid posterior approximation using surrogate-driven training of a lazy map [Brennan et al., NeurIPS, (2020)], i.e., a structure-exploiting transport map with low-dimensional nonlinearity. The trained lazy map then produces approximate posterior samples or density evaluations. Our surrogate construction is optimized for amortized Bayesian inversion using lazy map variational inference. We show that (i) the derivative-based reduced basis architecture [O'Leary-Roseberry et al., Comput. Methods Appl. Mech. Eng., 388 (2022)] minimizes the upper bound on the expected error in surrogate posterior approximation, and (ii) the derivative-informed training formulation [O'Leary-Roseberry et al., J. Comput. Phys., 496 (2024)] minimizes the expected error due to surrogate-driven transport map optimization. Our numerical results demonstrate that LazyDINO is highly efficient in cost amortization for Bayesian inversion. We observe one to two orders of magnitude reduction of offline cost for accurate posterior approximation, compared to simulation-based amortized inference via conditional transport and conventional surrogate-driven transport. In particular, LazyDINO outperforms Laplace approximation consistently using fewer than 1000 offline samples, while other amortized inference methods struggle and sometimes fail at 16,000 offline samples.
Fast Unconstrained Optimization via Hessian Averaging and Adaptive Gradient Sampling Methods
Aug 14, 2024
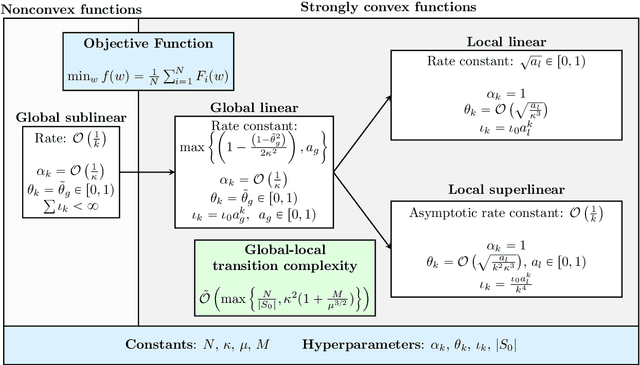


Abstract:We consider minimizing finite-sum and expectation objective functions via Hessian-averaging based subsampled Newton methods. These methods allow for gradient inexactness and have fixed per-iteration Hessian approximation costs. The recent work (Na et al. 2023) demonstrated that Hessian averaging can be utilized to achieve fast $\mathcal{O}\left(\sqrt{\tfrac{\log k}{k}}\right)$ local superlinear convergence for strongly convex functions in high probability, while maintaining fixed per-iteration Hessian costs. These methods, however, require gradient exactness and strong convexity, which poses challenges for their practical implementation. To address this concern we consider Hessian-averaged methods that allow gradient inexactness via norm condition based adaptive-sampling strategies. For the finite-sum problem we utilize deterministic sampling techniques which lead to global linear and sublinear convergence rates for strongly convex and nonconvex functions respectively. In this setting we are able to derive an improved deterministic local superlinear convergence rate of $\mathcal{O}\left(\tfrac{1}{k}\right)$. For the %expected risk expectation problem we utilize stochastic sampling techniques, and derive global linear and sublinear rates for strongly convex and nonconvex functions, as well as a $\mathcal{O}\left(\tfrac{1}{\sqrt{k}}\right)$ local superlinear convergence rate, all in expectation. We present novel analysis techniques that differ from the previous probabilistic results. Additionally, we propose scalable and efficient variations of these methods via diagonal approximations and derive the novel diagonally-averaged Newton (Dan) method for large-scale problems. Our numerical results demonstrate that the Hessian averaging not only helps with convergence, but can lead to state-of-the-art performance on difficult problems such as CIFAR100 classification with ResNets.
Efficient geometric Markov chain Monte Carlo for nonlinear Bayesian inversion enabled by derivative-informed neural operators
Mar 13, 2024Abstract:We propose an operator learning approach to accelerate geometric Markov chain Monte Carlo (MCMC) for solving infinite-dimensional nonlinear Bayesian inverse problems. While geometric MCMC employs high-quality proposals that adapt to posterior local geometry, it requires computing local gradient and Hessian information of the log-likelihood, incurring a high cost when the parameter-to-observable (PtO) map is defined through expensive model simulations. We consider a delayed-acceptance geometric MCMC method driven by a neural operator surrogate of the PtO map, where the proposal is designed to exploit fast surrogate approximations of the log-likelihood and, simultaneously, its gradient and Hessian. To achieve a substantial speedup, the surrogate needs to be accurate in predicting both the observable and its parametric derivative (the derivative of the observable with respect to the parameter). Training such a surrogate via conventional operator learning using input--output samples often demands a prohibitively large number of model simulations. In this work, we present an extension of derivative-informed operator learning [O'Leary-Roseberry et al., J. Comput. Phys., 496 (2024)] using input--output--derivative training samples. Such a learning method leads to derivative-informed neural operator (DINO) surrogates that accurately predict the observable and its parametric derivative at a significantly lower training cost than the conventional method. Cost and error analysis for reduced basis DINO surrogates are provided. Numerical studies on PDE-constrained Bayesian inversion demonstrate that DINO-driven MCMC generates effective posterior samples 3--9 times faster than geometric MCMC and 60--97 times faster than prior geometry-based MCMC. Furthermore, the training cost of DINO surrogates breaks even after collecting merely 10--25 effective posterior samples compared to geometric MCMC.
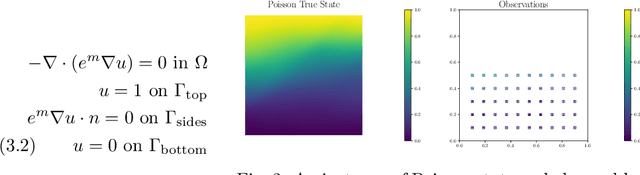
Efficient PDE-Constrained optimization under high-dimensional uncertainty using derivative-informed neural operators
May 31, 2023Abstract:We propose a novel machine learning framework for solving optimization problems governed by large-scale partial differential equations (PDEs) with high-dimensional random parameters. Such optimization under uncertainty (OUU) problems may be computational prohibitive using classical methods, particularly when a large number of samples is needed to evaluate risk measures at every iteration of an optimization algorithm, where each sample requires the solution of an expensive-to-solve PDE. To address this challenge, we propose a new neural operator approximation of the PDE solution operator that has the combined merits of (1) accurate approximation of not only the map from the joint inputs of random parameters and optimization variables to the PDE state, but also its derivative with respect to the optimization variables, (2) efficient construction of the neural network using reduced basis architectures that are scalable to high-dimensional OUU problems, and (3) requiring only a limited number of training data to achieve high accuracy for both the PDE solution and the OUU solution. We refer to such neural operators as multi-input reduced basis derivative informed neural operators (MR-DINOs). We demonstrate the accuracy and efficiency our approach through several numerical experiments, i.e. the risk-averse control of a semilinear elliptic PDE and the steady state Navier--Stokes equations in two and three spatial dimensions, each involving random field inputs. Across the examples, MR-DINOs offer $10^{3}$--$10^{7} \times$ reductions in execution time, and are able to produce OUU solutions of comparable accuracies to those from standard PDE based solutions while being over $10 \times$ more cost-efficient after factoring in the cost of construction.
Residual-based error correction for neural operator accelerated infinite-dimensional Bayesian inverse problems
Oct 06, 2022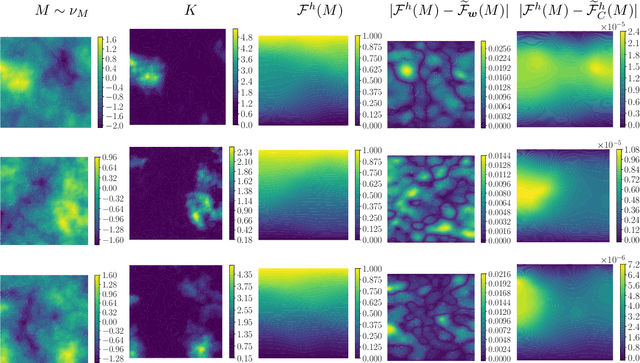
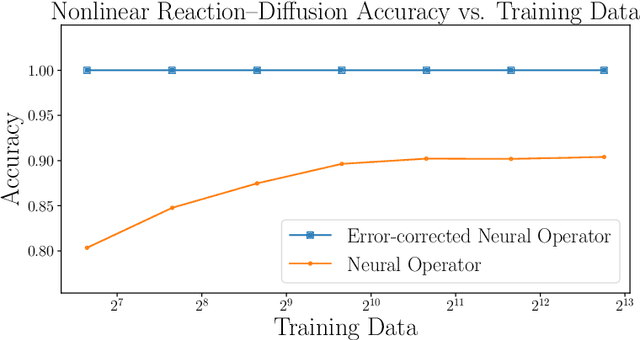
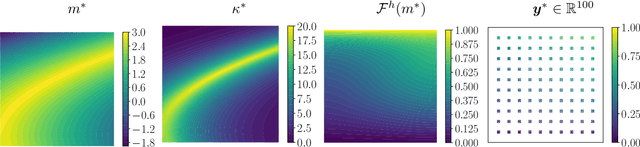

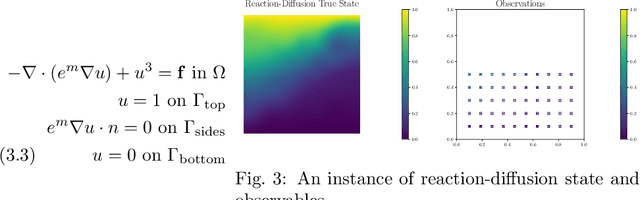
Abstract:We explore using neural operators, or neural network representations of nonlinear maps between function spaces, to accelerate infinite-dimensional Bayesian inverse problems (BIPs) with models governed by nonlinear parametric partial differential equations (PDEs). Neural operators have gained significant attention in recent years for their ability to approximate the parameter-to-solution maps defined by PDEs using as training data solutions of PDEs at a limited number of parameter samples. The computational cost of BIPs can be drastically reduced if the large number of PDE solves required for posterior characterization are replaced with evaluations of trained neural operators. However, reducing error in the resulting BIP solutions via reducing the approximation error of the neural operators in training can be challenging and unreliable. We provide an a priori error bound result that implies certain BIPs can be ill-conditioned to the approximation error of neural operators, thus leading to inaccessible accuracy requirements in training. To reliably deploy neural operators in BIPs, we consider a strategy for enhancing the performance of neural operators, which is to correct the prediction of a trained neural operator by solving a linear variational problem based on the PDE residual. We show that a trained neural operator with error correction can achieve a quadratic reduction of its approximation error, all while retaining substantial computational speedups of posterior sampling when models are governed by highly nonlinear PDEs. The strategy is applied to two numerical examples of BIPs based on a nonlinear reaction--diffusion problem and deformation of hyperelastic materials. We demonstrate that posterior representations of the two BIPs produced using trained neural operators are greatly and consistently enhanced by error correction.
Derivative-Informed Neural Operator: An Efficient Framework for High-Dimensional Parametric Derivative Learning
Jun 23, 2022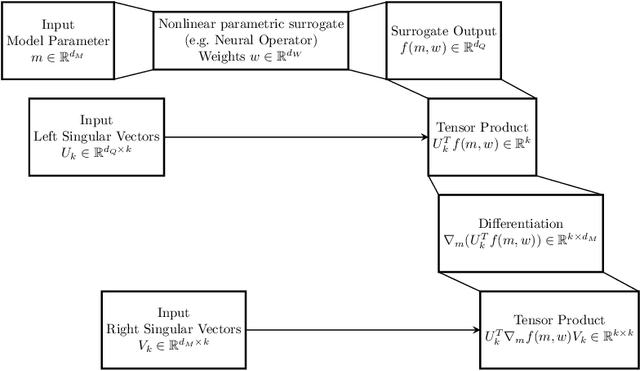
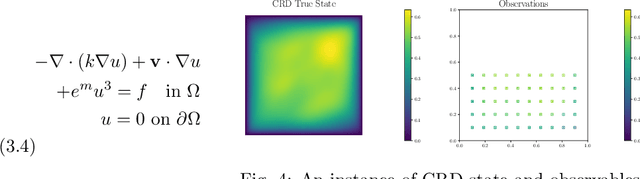
Abstract:Neural operators have gained significant attention recently due to their ability to approximate high-dimensional parametric maps between function spaces. At present, only parametric function approximation has been addressed in the neural operator literature. In this work we investigate incorporating parametric derivative information in neural operator training; this information can improve function approximations, additionally it can be used to improve the approximation of the derivative with respect to the parameter, which is often the key to scalable solution of high-dimensional outer-loop problems (e.g. Bayesian inverse problems). Parametric Jacobian information is formally intractable to incorporate due to its high-dimensionality, to address this concern we propose strategies based on reduced SVD, randomized sketching and the use of reduced basis surrogates. All of these strategies only require only $O(r)$ Jacobian actions to construct sample Jacobian data, and allow us to reduce the linear algebra and memory costs associated with the Jacobian training from the product of the input and output dimensions down to $O(r^2)$, where $r$ is the dimensionality associated with the dimension reduction technique. Numerical results for parametric PDE problems demonstrate that the addition of derivative information to the training problem can significantly improve the parametric map approximation, particularly given few data. When Jacobian actions are inexpensive compared to the parametric map, this information can be economically substituted for parametric map data. Additionally we show that Jacobian error approximations improve significantly with the introduction of Jacobian training data. This result opens the door to the use of derivative-informed neural operators (DINOs) in outer-loop algorithms where they can amortize the additional training data cost via repeated evaluations.
Adaptive Projected Residual Networks for Learning Parametric Maps from Sparse Data
Dec 14, 2021

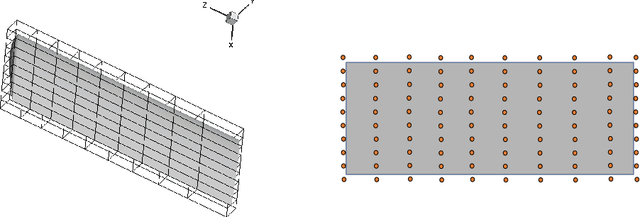
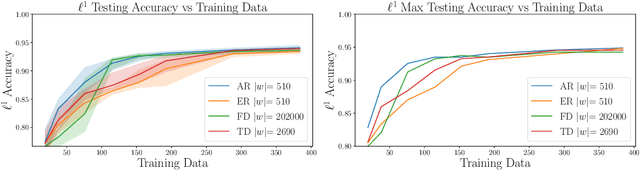
Abstract:We present a parsimonious surrogate framework for learning high dimensional parametric maps from limited training data. The need for parametric surrogates arises in many applications that require repeated queries of complex computational models. These applications include such "outer-loop" problems as Bayesian inverse problems, optimal experimental design, and optimal design and control under uncertainty, as well as real time inference and control problems. Many high dimensional parametric mappings admit low dimensional structure, which can be exploited by mapping-informed reduced bases of the inputs and outputs. Exploiting this property, we develop a framework for learning low dimensional approximations of such maps by adaptively constructing ResNet approximations between reduced bases of their inputs and output. Motivated by recent approximation theory for ResNets as discretizations of control flows, we prove a universal approximation property of our proposed adaptive projected ResNet framework, which motivates a related iterative algorithm for the ResNet construction. This strategy represents a confluence of the approximation theory and the algorithm since both make use of sequentially minimizing flows. In numerical examples we show that these parsimonious, mapping-informed architectures are able to achieve remarkably high accuracy given few training data, making them a desirable surrogate strategy to be implemented for minimal computational investment in training data generation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge