Estimating unknown parameters in differential equations with a reinforcement learning based PSO method

Differential equations offer a foundational yet powerful framework for modeling interactions within complex dynamic systems and are widely applied across numerous scientific fields. One common challenge in this area is estimating the unknown parameters of these dynamic relationships. However, traditional numerical optimization methods rely on the selection of initial parameter values, making them prone to local optima. Meanwhile, deep learning and Bayesian methods require training models on specific differential equations, resulting in poor versatility. This paper reformulates the parameter estimation problem of differential equations as an optimization problem by introducing the concept of particles from the particle swarm optimization algorithm. Building on reinforcement learning-based particle swarm optimization (RLLPSO), this paper proposes a novel method, DERLPSO, for estimating unknown parameters of differential equations. We compared its performance on three typical ordinary differential equations with the state-of-the-art methods, including the RLLPSO algorithm, traditional numerical methods, deep learning approaches, and Bayesian methods. The experimental results demonstrate that our DERLPSO consistently outperforms other methods in terms of performance, achieving an average Mean Square Error of 1.13e-05, which reduces the error by approximately 4 orders of magnitude compared to other methods. Apart from ordinary differential equations, our DERLPSO also show great promise for estimating unknown parameters of partial differential equations. The DERLPSO method proposed in this paper has high accuracy, is independent of initial parameter values, and possesses strong versatility and stability. This work provides new insights into unknown parameter estimation for differential equations.

PhyloTransformer: A Discriminative Model for Mutation Prediction Based on a Multi-head Self-attention Mechanism

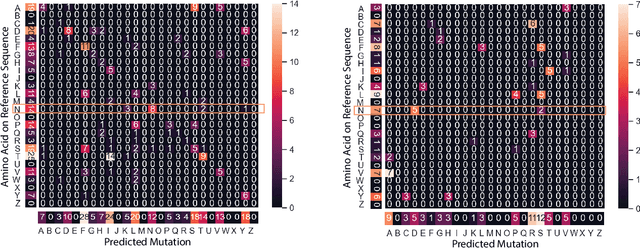
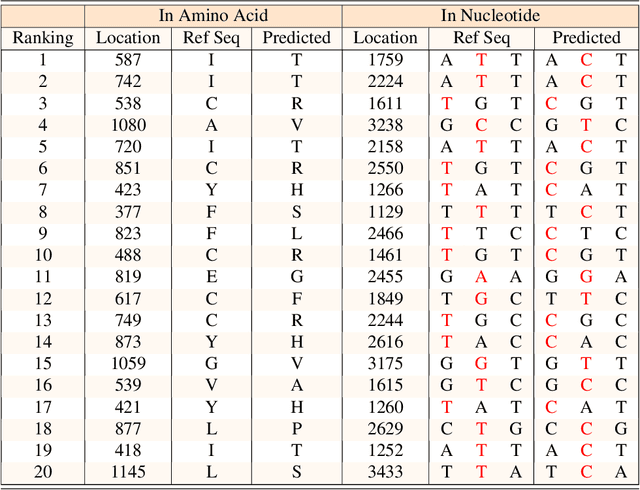
Severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) has caused an ongoing pandemic infecting 219 million people as of 10/19/21, with a 3.6% mortality rate. Natural selection can generate favorable mutations with improved fitness advantages; however, the identified coronaviruses may be the tip of the iceberg, and potentially more fatal variants of concern (VOCs) may emerge over time. Understanding the patterns of emerging VOCs and forecasting mutations that may lead to gain of function or immune escape is urgently required. Here we developed PhyloTransformer, a Transformer-based discriminative model that engages a multi-head self-attention mechanism to model genetic mutations that may lead to viral reproductive advantage. In order to identify complex dependencies between the elements of each input sequence, PhyloTransformer utilizes advanced modeling techniques, including a novel Fast Attention Via positive Orthogonal Random features approach (FAVOR+) from Performer, and the Masked Language Model (MLM) from Bidirectional Encoder Representations from Transformers (BERT). PhyloTransformer was trained with 1,765,297 genetic sequences retrieved from the Global Initiative for Sharing All Influenza Data (GISAID) database. Firstly, we compared the prediction accuracy of novel mutations and novel combinations using extensive baseline models; we found that PhyloTransformer outperformed every baseline method with statistical significance. Secondly, we examined predictions of mutations in each nucleotide of the receptor binding motif (RBM), and we found our predictions were precise and accurate. Thirdly, we predicted modifications of N-glycosylation sites to identify mutations associated with altered glycosylation that may be favored during viral evolution. We anticipate that PhyloTransformer may guide proactive vaccine design for effective targeting of future SARS-CoV-2 variants.

Graph Laplacians, Riemannian Manifolds and their Machine-Learning

Graph Laplacians as well as related spectral inequalities and (co-)homology provide a foray into discrete analogues of Riemannian manifolds, providing a rich interplay between combinatorics, geometry and theoretical physics. We apply some of the latest techniques in data science such as supervised and unsupervised machine-learning and topological data analysis to the Wolfram database of some 8000 finite graphs in light of studying these correspondences. Encouragingly, we find that neural classifiers, regressors and networks can perform, with high efficiently and accuracy, a multitude of tasks ranging from recognizing graph Ricci-flatness, to predicting the spectral gap, to detecting the presence of Hamiltonian cycles, etc.

AE-OT-GAN: Training GANs from data specific latent distribution

Though generative adversarial networks (GANs) areprominent models to generate realistic and crisp images,they often encounter the mode collapse problems and arehard to train, which comes from approximating the intrinsicdiscontinuous distribution transform map with continuousDNNs. The recently proposed AE-OT model addresses thisproblem by explicitly computing the discontinuous distribu-tion transform map through solving a semi-discrete optimaltransport (OT) map in the latent space of the autoencoder.However the generated images are blurry. In this paper, wepropose the AE-OT-GAN model to utilize the advantages ofthe both models: generate high quality images and at thesame time overcome the mode collapse/mixture problems.Specifically, we first faithfully embed the low dimensionalimage manifold into the latent space by training an autoen-coder (AE). Then we compute the optimal transport (OT)map that pushes forward the uniform distribution to the la-tent distribution supported on the latent manifold. Finally,our GAN model is trained to generate high quality imagesfrom the latent distribution, the distribution transform mapfrom which to the empirical data distribution will be con-tinuous. The paired data between the latent code and thereal images gives us further constriction about the generator.Experiments on simple MNIST dataset and complex datasetslike Cifar-10 and CelebA show the efficacy and efficiency ofour proposed method.

Mode Collapse and Regularity of Optimal Transportation Maps

This work builds the connection between the regularity theory of optimal transportation map, Monge-Amp\`{e}re equation and GANs, which gives a theoretic understanding of the major drawbacks of GANs: convergence difficulty and mode collapse. According to the regularity theory of Monge-Amp\`{e}re equation, if the support of the target measure is disconnected or just non-convex, the optimal transportation mapping is discontinuous. General DNNs can only approximate continuous mappings. This intrinsic conflict leads to the convergence difficulty and mode collapse in GANs. We test our hypothesis that the supports of real data distribution are in general non-convex, therefore the discontinuity is unavoidable using an Autoencoder combined with discrete optimal transportation map (AE-OT framework) on the CelebA data set. The testing result is positive. Furthermore, we propose to approximate the continuous Brenier potential directly based on discrete Brenier theory to tackle mode collapse. Comparing with existing method, this method is more accurate and effective.

Latent Space Optimal Transport for Generative Models

Variational Auto-Encoders enforce their learned intermediate latent-space data distribution to be a simple distribution, such as an isotropic Gaussian. However, this causes the posterior collapse problem and loses manifold structure which can be important for datasets such as facial images. A GAN can transform a simple distribution to a latent-space data distribution and thus preserve the manifold structure, but optimizing a GAN involves solving a Min-Max optimization problem, which is difficult and not well understood so far. Therefore, we propose a GAN-like method to transform a simple distribution to a data distribution in the latent space by solving only a minimization problem. This minimization problem comes from training a discriminator between a simple distribution and a latent-space data distribution. Then, we can explicitly formulate an Optimal Transport (OT) problem that computes the desired mapping between the two distributions. This means that we can transform a distribution without solving the difficult Min-Max optimization problem. Experimental results on an eight-Gaussian dataset show that the proposed OT can handle multi-cluster distributions. Results on the MNIST and the CelebA datasets validate the effectiveness of the proposed method.

Geometric Understanding of Deep Learning

Deep learning is the mainstream technique for many machine learning tasks, including image recognition, machine translation, speech recognition, and so on. It has outperformed conventional methods in various fields and achieved great successes. Unfortunately, the understanding on how it works remains unclear. It has the central importance to lay down the theoretic foundation for deep learning. In this work, we give a geometric view to understand deep learning: we show that the fundamental principle attributing to the success is the manifold structure in data, namely natural high dimensional data concentrates close to a low-dimensional manifold, deep learning learns the manifold and the probability distribution on it. We further introduce the concepts of rectified linear complexity for deep neural network measuring its learning capability, rectified linear complexity of an embedding manifold describing the difficulty to be learned. Then we show for any deep neural network with fixed architecture, there exists a manifold that cannot be learned by the network. Finally, we propose to apply optimal mass transportation theory to control the probability distribution in the latent space.

A Geometric View of Optimal Transportation and Generative Model

In this work, we show the intrinsic relations between optimal transportation and convex geometry, especially the variational approach to solve Alexandrov problem: constructing a convex polytope with prescribed face normals and volumes. This leads to a geometric interpretation to generative models, and leads to a novel framework for generative models. By using the optimal transportation view of GAN model, we show that the discriminator computes the Kantorovich potential, the generator calculates the transportation map. For a large class of transportation costs, the Kantorovich potential can give the optimal transportation map by a close-form formula. Therefore, it is sufficient to solely optimize the discriminator. This shows the adversarial competition can be avoided, and the computational architecture can be simplified. Preliminary experimental results show the geometric method outperforms WGAN for approximating probability measures with multiple clusters in low dimensional space.