EMO-R3: Reflective Reinforcement Learning for Emotional Reasoning in Multimodal Large Language Models

Multimodal Large Language Models (MLLMs) have shown remarkable progress in visual reasoning and understanding tasks but still struggle to capture the complexity and subjectivity of human emotions. Existing approaches based on supervised fine-tuning often suffer from limited generalization and poor interpretability, while reinforcement learning methods such as Group Relative Policy Optimization fail to align with the intrinsic characteristics of emotional cognition. To address these challenges, we propose Reflective Reinforcement Learning for Emotional Reasoning (EMO-R3), a framework designed to enhance the emotional reasoning ability of MLLMs. Specifically, we introduce Structured Emotional Thinking to guide the model to perform step-by-step emotional reasoning in a structured and interpretable manner, and design a Reflective Emotional Reward that enables the model to re-evaluate its reasoning based on visual-text consistency and emotional coherence. Extensive experiments demonstrate that EMO-R3 significantly improves both the interpretability and emotional intelligence of MLLMs, achieving superior performance across multiple visual emotional understanding benchmarks.

Improving Heterogeneous Model Reuse by Density Estimation

This paper studies multiparty learning, aiming to learn a model using the private data of different participants. Model reuse is a promising solution for multiparty learning, assuming that a local model has been trained for each party. Considering the potential sample selection bias among different parties, some heterogeneous model reuse approaches have been developed. However, although pre-trained local classifiers are utilized in these approaches, the characteristics of the local data are not well exploited. This motivates us to estimate the density of local data and design an auxiliary model together with the local classifiers for reuse. To address the scenarios where some local models are not well pre-trained, we further design a multiparty cross-entropy loss for calibration. Upon existing works, we address a challenging problem of heterogeneous model reuse from a decision theory perspective and take advantage of recent advances in density estimation. Experimental results on both synthetic and benchmark data demonstrate the superiority of the proposed method.

FedABC: Targeting Fair Competition in Personalized Federated Learning

Federated learning aims to collaboratively train models without accessing their client's local private data. The data may be Non-IID for different clients and thus resulting in poor performance. Recently, personalized federated learning (PFL) has achieved great success in handling Non-IID data by enforcing regularization in local optimization or improving the model aggregation scheme on the server. However, most of the PFL approaches do not take into account the unfair competition issue caused by the imbalanced data distribution and lack of positive samples for some classes in each client. To address this issue, we propose a novel and generic PFL framework termed Federated Averaging via Binary Classification, dubbed FedABC. In particular, we adopt the ``one-vs-all'' training strategy in each client to alleviate the unfair competition between classes by constructing a personalized binary classification problem for each class. This may aggravate the class imbalance challenge and thus a novel personalized binary classification loss that incorporates both the under-sampling and hard sample mining strategies is designed. Extensive experiments are conducted on two popular datasets under different settings, and the results demonstrate that our FedABC can significantly outperform the existing counterparts.

A Geometric View of Optimal Transportation and Generative Model

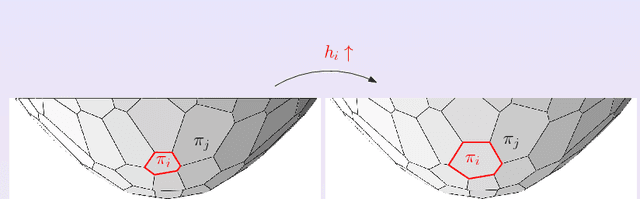
In this work, we show the intrinsic relations between optimal transportation and convex geometry, especially the variational approach to solve Alexandrov problem: constructing a convex polytope with prescribed face normals and volumes. This leads to a geometric interpretation to generative models, and leads to a novel framework for generative models. By using the optimal transportation view of GAN model, we show that the discriminator computes the Kantorovich potential, the generator calculates the transportation map. For a large class of transportation costs, the Kantorovich potential can give the optimal transportation map by a close-form formula. Therefore, it is sufficient to solely optimize the discriminator. This shows the adversarial competition can be avoided, and the computational architecture can be simplified. Preliminary experimental results show the geometric method outperforms WGAN for approximating probability measures with multiple clusters in low dimensional space.