X$^{2}$-Gaussian: 4D Radiative Gaussian Splatting for Continuous-time Tomographic Reconstruction

Four-dimensional computed tomography (4D CT) reconstruction is crucial for capturing dynamic anatomical changes but faces inherent limitations from conventional phase-binning workflows. Current methods discretize temporal resolution into fixed phases with respiratory gating devices, introducing motion misalignment and restricting clinical practicality. In this paper, We propose X$^2$-Gaussian, a novel framework that enables continuous-time 4D-CT reconstruction by integrating dynamic radiative Gaussian splatting with self-supervised respiratory motion learning. Our approach models anatomical dynamics through a spatiotemporal encoder-decoder architecture that predicts time-varying Gaussian deformations, eliminating phase discretization. To remove dependency on external gating devices, we introduce a physiology-driven periodic consistency loss that learns patient-specific breathing cycles directly from projections via differentiable optimization. Extensive experiments demonstrate state-of-the-art performance, achieving a 9.93 dB PSNR gain over traditional methods and 2.25 dB improvement against prior Gaussian splatting techniques. By unifying continuous motion modeling with hardware-free period learning, X$^2$-Gaussian advances high-fidelity 4D CT reconstruction for dynamic clinical imaging. Project website at: https://x2-gaussian.github.io/.

X-LRM: X-ray Large Reconstruction Model for Extremely Sparse-View Computed Tomography Recovery in One Second

Sparse-view 3D CT reconstruction aims to recover volumetric structures from a limited number of 2D X-ray projections. Existing feedforward methods are constrained by the limited capacity of CNN-based architectures and the scarcity of large-scale training datasets. In this paper, we propose an X-ray Large Reconstruction Model (X-LRM) for extremely sparse-view (<10 views) CT reconstruction. X-LRM consists of two key components: X-former and X-triplane. Our X-former can handle an arbitrary number of input views using an MLP-based image tokenizer and a Transformer-based encoder. The output tokens are then upsampled into our X-triplane representation, which models the 3D radiodensity as an implicit neural field. To support the training of X-LRM, we introduce Torso-16K, a large-scale dataset comprising over 16K volume-projection pairs of various torso organs. Extensive experiments demonstrate that X-LRM outperforms the state-of-the-art method by 1.5 dB and achieves 27x faster speed and better flexibility. Furthermore, the downstream evaluation of lung segmentation tasks also suggests the practical value of our approach. Our code, pre-trained models, and dataset will be released at https://github.com/caiyuanhao1998/X-LRM

Three-Dimensional MRI Reconstruction with Gaussian Representations: Tackling the Undersampling Problem

Three-Dimensional Gaussian Splatting (3DGS) has shown substantial promise in the field of computer vision, but remains unexplored in the field of magnetic resonance imaging (MRI). This study explores its potential for the reconstruction of isotropic resolution 3D MRI from undersampled k-space data. We introduce a novel framework termed 3D Gaussian MRI (3DGSMR), which employs 3D Gaussian distributions as an explicit representation for MR volumes. Experimental evaluations indicate that this method can effectively reconstruct voxelized MR images, achieving a quality on par with that of well-established 3D MRI reconstruction techniques found in the literature. Notably, the 3DGSMR scheme operates under a self-supervised framework, obviating the need for extensive training datasets or prior model training. This approach introduces significant innovations to the domain, notably the adaptation of 3DGS to MRI reconstruction and the novel application of the existing 3DGS methodology to decompose MR signals, which are presented in a complex-valued format.

4DRGS: 4D Radiative Gaussian Splatting for Efficient 3D Vessel Reconstruction from Sparse-View Dynamic DSA Images

Reconstructing 3D vessel structures from sparse-view dynamic digital subtraction angiography (DSA) images enables accurate medical assessment while reducing radiation exposure. Existing methods often produce suboptimal results or require excessive computation time. In this work, we propose 4D radiative Gaussian splatting (4DRGS) to achieve high-quality reconstruction efficiently. In detail, we represent the vessels with 4D radiative Gaussian kernels. Each kernel has time-invariant geometry parameters, including position, rotation, and scale, to model static vessel structures. The time-dependent central attenuation of each kernel is predicted from a compact neural network to capture the temporal varying response of contrast agent flow. We splat these Gaussian kernels to synthesize DSA images via X-ray rasterization and optimize the model with real captured ones. The final 3D vessel volume is voxelized from the well-trained kernels. Moreover, we introduce accumulated attenuation pruning and bounded scaling activation to improve reconstruction quality. Extensive experiments on real-world patient data demonstrate that 4DRGS achieves impressive results in 5 minutes training, which is 32x faster than the state-of-the-art method. This underscores the potential of 4DRGS for real-world clinics.

R$^2$-Gaussian: Rectifying Radiative Gaussian Splatting for Tomographic Reconstruction

3D Gaussian splatting (3DGS) has shown promising results in image rendering and surface reconstruction. However, its potential in volumetric reconstruction tasks, such as X-ray computed tomography, remains under-explored. This paper introduces R2-Gaussian, the first 3DGS-based framework for sparse-view tomographic reconstruction. By carefully deriving X-ray rasterization functions, we discover a previously unknown integration bias in the standard 3DGS formulation, which hampers accurate volume retrieval. To address this issue, we propose a novel rectification technique via refactoring the projection from 3D to 2D Gaussians. Our new method presents three key innovations: (1) introducing tailored Gaussian kernels, (2) extending rasterization to X-ray imaging, and (3) developing a CUDA-based differentiable voxelizer. Extensive experiments demonstrate that our method outperforms state-of-the-art approaches by 0.93 dB in PSNR and 0.014 in SSIM. Crucially, it delivers high-quality results in 3 minutes, which is 12x faster than NeRF-based methods and on par with traditional algorithms. The superior performance and rapid convergence of our method highlight its practical value.

EndoSurf: Neural Surface Reconstruction of Deformable Tissues with Stereo Endoscope Videos

Reconstructing soft tissues from stereo endoscope videos is an essential prerequisite for many medical applications. Previous methods struggle to produce high-quality geometry and appearance due to their inadequate representations of 3D scenes. To address this issue, we propose a novel neural-field-based method, called EndoSurf, which effectively learns to represent a deforming surface from an RGBD sequence. In EndoSurf, we model surface dynamics, shape, and texture with three neural fields. First, 3D points are transformed from the observed space to the canonical space using the deformation field. The signed distance function (SDF) field and radiance field then predict their SDFs and colors, respectively, with which RGBD images can be synthesized via differentiable volume rendering. We constrain the learned shape by tailoring multiple regularization strategies and disentangling geometry and appearance. Experiments on public endoscope datasets demonstrate that EndoSurf significantly outperforms existing solutions, particularly in reconstructing high-fidelity shapes. Code is available at https://github.com/Ruyi-Zha/endosurf.git.

NAF: Neural Attenuation Fields for Sparse-View CBCT Reconstruction

This paper proposes a novel and fast self-supervised solution for sparse-view CBCT reconstruction (Cone Beam Computed Tomography) that requires no external training data. Specifically, the desired attenuation coefficients are represented as a continuous function of 3D spatial coordinates, parameterized by a fully-connected deep neural network. We synthesize projections discretely and train the network by minimizing the error between real and synthesized projections. A learning-based encoder entailing hash coding is adopted to help the network capture high-frequency details. This encoder outperforms the commonly used frequency-domain encoder in terms of having higher performance and efficiency, because it exploits the smoothness and sparsity of human organs. Experiments have been conducted on both human organ and phantom datasets. The proposed method achieves state-of-the-art accuracy and spends reasonably short computation time.

PlueckerNet: Learn to Register 3D Line Reconstructions

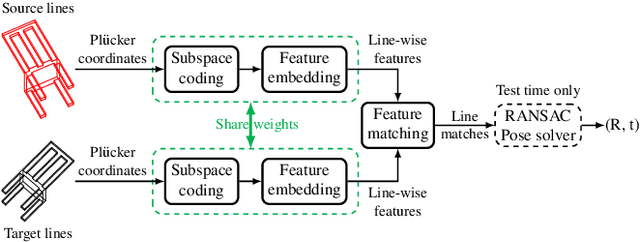
Aligning two partially-overlapped 3D line reconstructions in Euclidean space is challenging, as we need to simultaneously solve correspondences and relative pose between line reconstructions. This paper proposes a neural network based method and it has three modules connected in sequence: (i) a Multilayer Perceptron (MLP) based network takes Pluecker representations of lines as inputs, to extract discriminative line-wise features and matchabilities (how likely each line is going to have a match), (ii) an Optimal Transport (OT) layer takes two-view line-wise features and matchabilities as inputs to estimate a 2D joint probability matrix, with each item describes the matchness of a line pair, and (iii) line pairs with Top-K matching probabilities are fed to a 2-line minimal solver in a RANSAC framework to estimate a six Degree-of-Freedom (6-DoF) rigid transformation. Experiments on both indoor and outdoor datasets show that the registration (rotation and translation) precision of our method outperforms baselines significantly.