FARM: Frequency-Aware Model for Cross-Domain Live-Streaming Recommendation

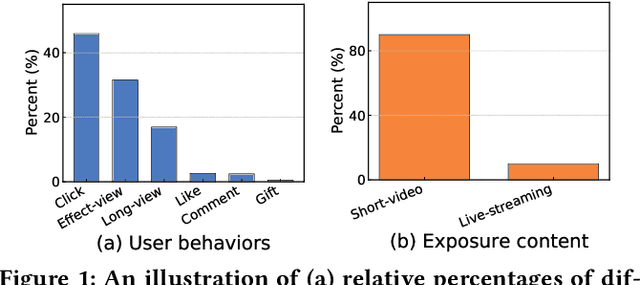
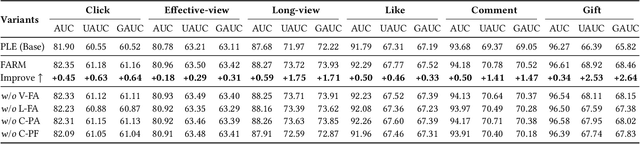
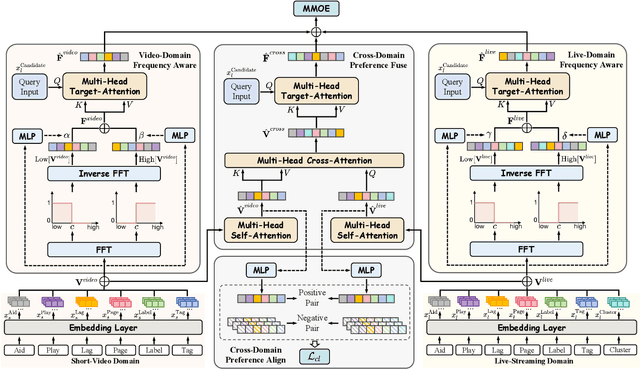
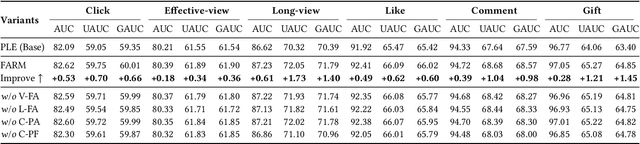
Live-streaming services have attracted widespread popularity due to their real-time interactivity and entertainment value. Users can engage with live-streaming authors by participating in live chats, posting likes, or sending virtual gifts to convey their preferences and support. However, the live-streaming services faces serious data-sparsity problem, which can be attributed to the following two points: (1) User's valuable behaviors are usually sparse, e.g., like, comment and gift, which are easily overlooked by the model, making it difficult to describe user's personalized preference. (2) The main exposure content on our platform is short-video, which is 9 times higher than the exposed live-streaming, leading to the inability of live-streaming content to fully model user preference. To this end, we propose a Frequency-Aware Model for Cross-Domain Live-Streaming Recommendation, termed as FARM. Specifically, we first present the intra-domain frequency aware module to enable our model to perceive user's sparse yet valuable behaviors, i.e., high-frequency information, supported by the Discrete Fourier Transform (DFT). To transfer user preference across the short-video and live-streaming domains, we propose a novel preference align before fuse strategy, which consists of two parts: the cross-domain preference align module to align user preference in both domains with contrastive learning, and the cross-domain preference fuse module to further fuse user preference in both domains using a serious of tailor-designed attention mechanisms. Extensive offline experiments and online A/B testing on Kuaishou live-streaming services demonstrate the effectiveness and superiority of FARM. Our FARM has been deployed in online live-streaming services and currently serves hundreds of millions of users on Kuaishou.

Exploring Edge Probability Graph Models Beyond Edge Independency: Concepts, Analyses, and Algorithms

Desirable random graph models (RGMs) should (i) be tractable so that we can compute and control graph statistics, and (ii) generate realistic structures such as high clustering (i.e., high subgraph densities). A popular category of RGMs (e.g., Erdos-Renyi and stochastic Kronecker) outputs edge probabilities, and we need to realize (i.e., sample from) the edge probabilities to generate graphs. Typically, each edge (in)existence is assumed to be determined independently. However, with edge independency, RGMs theoretically cannot produce high subgraph densities unless they "replicate" input graphs. In this work, we explore realization beyond edge independence that can produce more realistic structures while ensuring high tractability. Specifically, we propose edge-dependent realization schemes called binding and derive closed-form tractability results on subgraph (e.g., triangle) densities in graphs generated with binding. We propose algorithms for graph generation with binding and parameter fitting of binding. We empirically validate that binding exhibits high tractability and generates realistic graphs with high clustering, significantly improving upon existing RGMs assuming edge independency.

Coupled Multiwavelet Neural Operator Learning for Coupled Partial Differential Equations

Coupled partial differential equations (PDEs) are key tasks in modeling the complex dynamics of many physical processes. Recently, neural operators have shown the ability to solve PDEs by learning the integral kernel directly in Fourier/Wavelet space, so the difficulty for solving the coupled PDEs depends on dealing with the coupled mappings between the functions. Towards this end, we propose a \textit{coupled multiwavelets neural operator} (CMWNO) learning scheme by decoupling the coupled integral kernels during the multiwavelet decomposition and reconstruction procedures in the Wavelet space. The proposed model achieves significantly higher accuracy compared to previous learning-based solvers in solving the coupled PDEs including Gray-Scott (GS) equations and the non-local mean field game (MFG) problem. According to our experimental results, the proposed model exhibits a $2\times \sim 4\times$ improvement relative $L$2 error compared to the best results from the state-of-the-art models.

Data-driven Perception of Neuron Point Process with Unknown Unknowns

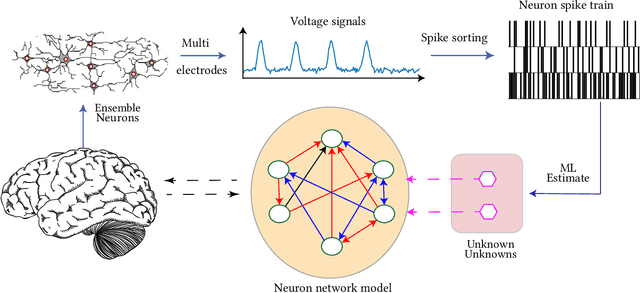
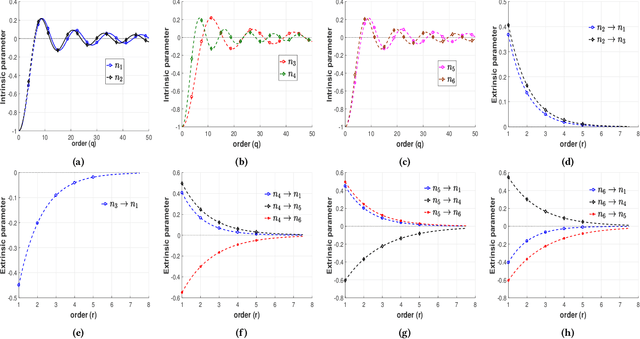
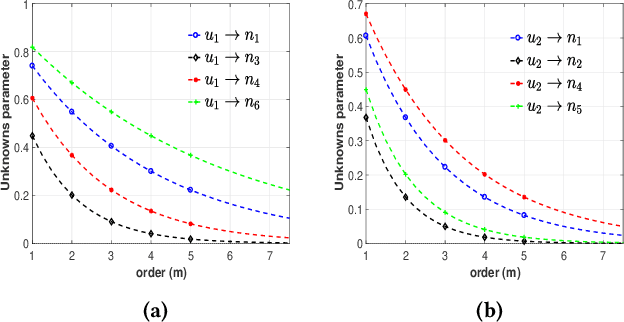
Identification of patterns from discrete data time-series for statistical inference, threat detection, social opinion dynamics, brain activity prediction has received recent momentum. In addition to the huge data size, the associated challenges are, for example, (i) missing data to construct a closed time-varying complex network, and (ii) contribution of unknown sources which are not probed. Towards this end, the current work focuses on statistical neuron system model with multi-covariates and unknown inputs. Previous research of neuron activity analysis is mainly limited with effects from the spiking history of target neuron and the interaction with other neurons in the system while ignoring the influence of unknown stimuli. We propose to use unknown unknowns, which describes the effect of unknown stimuli, undetected neuron activities and all other hidden sources of error. The maximum likelihood estimation with the fixed-point iteration method is implemented. The fixed-point iterations converge fast, and the proposed methods can be efficiently parallelized and offer computational advantage especially when the input spiking trains are over long time-horizon. The developed framework provides an intuition into the meaning of having extra degrees-of-freedom in the data to support the need for unknowns. The proposed algorithm is applied to simulated spike trains and on real-world experimental data of mouse somatosensory, mouse retina and cat retina. The model shows a successful increasing of system likelihood with respect to the conditional intensity function, and it also reveals the convergence with iterations. Results suggest that the neural connection model with unknown unknowns can efficiently estimate the statistical properties of the process by increasing the network likelihood.