Data-driven Perception of Neuron Point Process with Unknown Unknowns
Paper and Code
Nov 02, 2018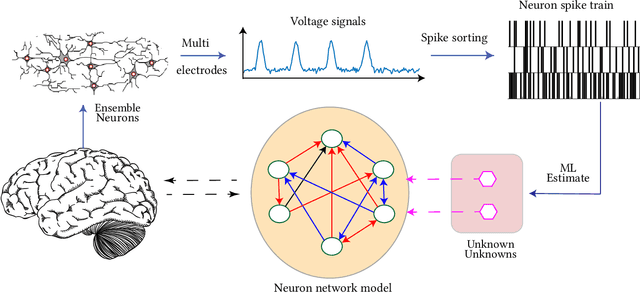

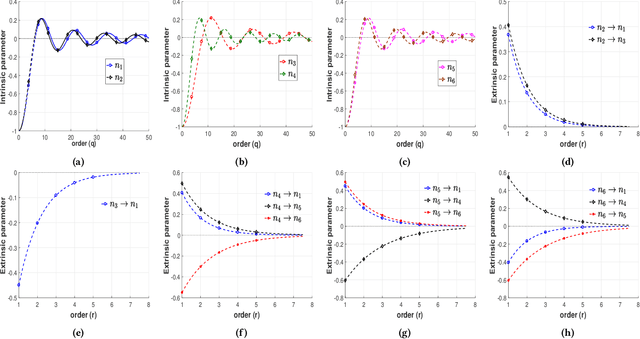
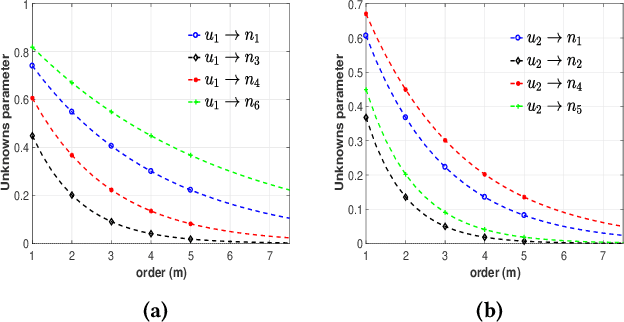
Identification of patterns from discrete data time-series for statistical inference, threat detection, social opinion dynamics, brain activity prediction has received recent momentum. In addition to the huge data size, the associated challenges are, for example, (i) missing data to construct a closed time-varying complex network, and (ii) contribution of unknown sources which are not probed. Towards this end, the current work focuses on statistical neuron system model with multi-covariates and unknown inputs. Previous research of neuron activity analysis is mainly limited with effects from the spiking history of target neuron and the interaction with other neurons in the system while ignoring the influence of unknown stimuli. We propose to use unknown unknowns, which describes the effect of unknown stimuli, undetected neuron activities and all other hidden sources of error. The maximum likelihood estimation with the fixed-point iteration method is implemented. The fixed-point iterations converge fast, and the proposed methods can be efficiently parallelized and offer computational advantage especially when the input spiking trains are over long time-horizon. The developed framework provides an intuition into the meaning of having extra degrees-of-freedom in the data to support the need for unknowns. The proposed algorithm is applied to simulated spike trains and on real-world experimental data of mouse somatosensory, mouse retina and cat retina. The model shows a successful increasing of system likelihood with respect to the conditional intensity function, and it also reveals the convergence with iterations. Results suggest that the neural connection model with unknown unknowns can efficiently estimate the statistical properties of the process by increasing the network likelihood.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge