Multi-scale Generative Modeling for Fast Sampling

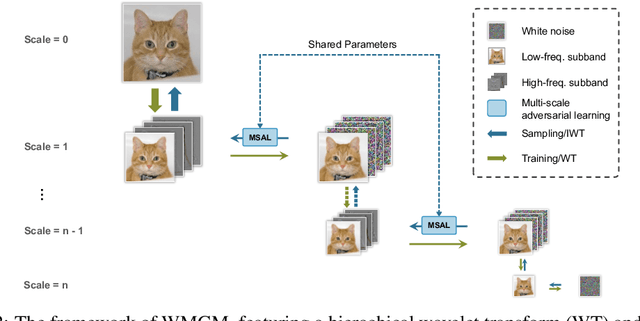
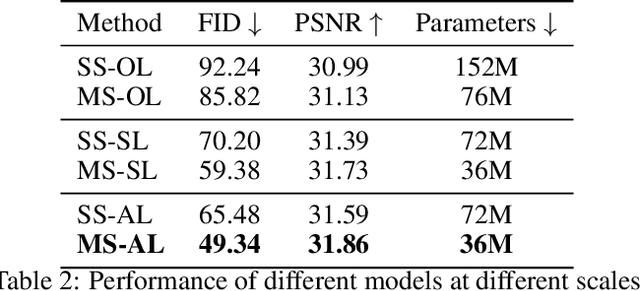
While working within the spatial domain can pose problems associated with ill-conditioned scores caused by power-law decay, recent advances in diffusion-based generative models have shown that transitioning to the wavelet domain offers a promising alternative. However, within the wavelet domain, we encounter unique challenges, especially the sparse representation of high-frequency coefficients, which deviates significantly from the Gaussian assumptions in the diffusion process. To this end, we propose a multi-scale generative modeling in the wavelet domain that employs distinct strategies for handling low and high-frequency bands. In the wavelet domain, we apply score-based generative modeling with well-conditioned scores for low-frequency bands, while utilizing a multi-scale generative adversarial learning for high-frequency bands. As supported by the theoretical analysis and experimental results, our model significantly improve performance and reduce the number of trainable parameters, sampling steps, and time.

Neuro-Inspired Information-Theoretic Hierarchical Perception for Multimodal Learning

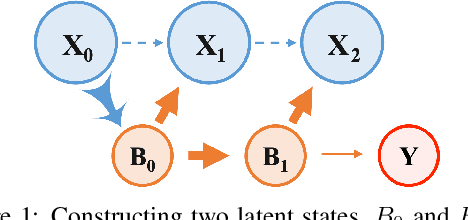
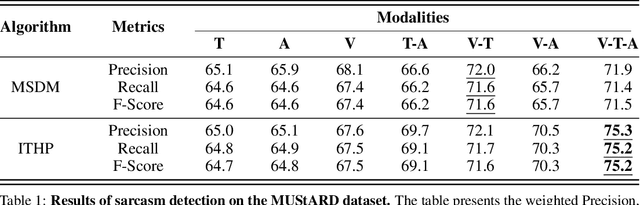
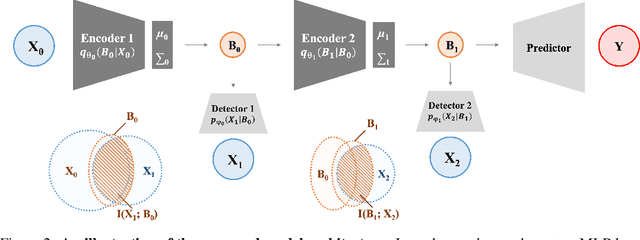
Integrating and processing information from various sources or modalities are critical for obtaining a comprehensive and accurate perception of the real world in autonomous systems and cyber-physical systems. Drawing inspiration from neuroscience, we develop the Information-Theoretic Hierarchical Perception (ITHP) model, which utilizes the concept of information bottleneck. Different from most traditional fusion models that incorporate all modalities identically in neural networks, our model designates a prime modality and regards the remaining modalities as detectors in the information pathway, serving to distill the flow of information. Our proposed perception model focuses on constructing an effective and compact information flow by achieving a balance between the minimization of mutual information between the latent state and the input modal state, and the maximization of mutual information between the latent states and the remaining modal states. This approach leads to compact latent state representations that retain relevant information while minimizing redundancy, thereby substantially enhancing the performance of multimodal representation learning. Experimental evaluations on the MUStARD, CMU-MOSI, and CMU-MOSEI datasets demonstrate that our model consistently distills crucial information in multimodal learning scenarios, outperforming state-of-the-art benchmarks. Remarkably, on the CMU-MOSI dataset, ITHP surpasses human-level performance in the multimodal sentiment binary classification task across all evaluation metrics (i.e., Binary Accuracy, F1 Score, Mean Absolute Error, and Pearson Correlation).

Neuro-Inspired Hierarchical Multimodal Learning

Integrating and processing information from various sources or modalities are critical for obtaining a comprehensive and accurate perception of the real world. Drawing inspiration from neuroscience, we develop the Information-Theoretic Hierarchical Perception (ITHP) model, which utilizes the concept of information bottleneck. Distinct from most traditional fusion models that aim to incorporate all modalities as input, our model designates the prime modality as input, while the remaining modalities act as detectors in the information pathway. Our proposed perception model focuses on constructing an effective and compact information flow by achieving a balance between the minimization of mutual information between the latent state and the input modal state, and the maximization of mutual information between the latent states and the remaining modal states. This approach leads to compact latent state representations that retain relevant information while minimizing redundancy, thereby substantially enhancing the performance of downstream tasks. Experimental evaluations on both the MUStARD and CMU-MOSI datasets demonstrate that our model consistently distills crucial information in multimodal learning scenarios, outperforming state-of-the-art benchmarks.

Coupled Multiwavelet Neural Operator Learning for Coupled Partial Differential Equations

Coupled partial differential equations (PDEs) are key tasks in modeling the complex dynamics of many physical processes. Recently, neural operators have shown the ability to solve PDEs by learning the integral kernel directly in Fourier/Wavelet space, so the difficulty for solving the coupled PDEs depends on dealing with the coupled mappings between the functions. Towards this end, we propose a \textit{coupled multiwavelets neural operator} (CMWNO) learning scheme by decoupling the coupled integral kernels during the multiwavelet decomposition and reconstruction procedures in the Wavelet space. The proposed model achieves significantly higher accuracy compared to previous learning-based solvers in solving the coupled PDEs including Gray-Scott (GS) equations and the non-local mean field game (MFG) problem. According to our experimental results, the proposed model exhibits a $2\times \sim 4\times$ improvement relative $L$2 error compared to the best results from the state-of-the-art models.