Multi-scale Generative Modeling for Fast Sampling

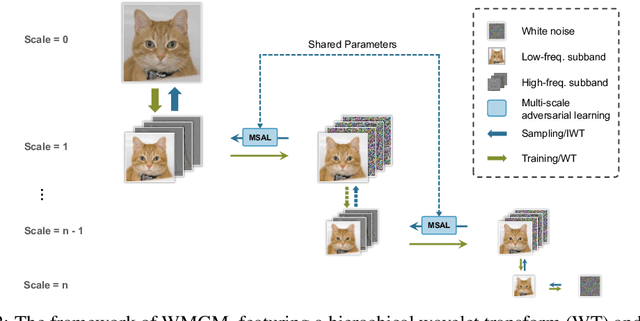
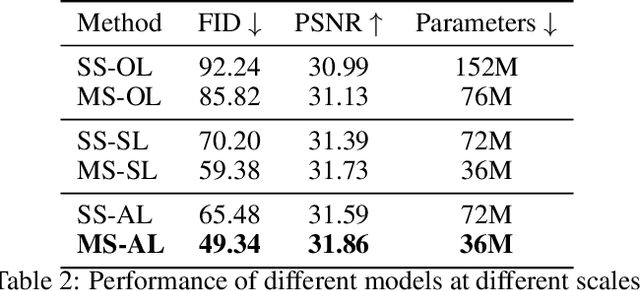
While working within the spatial domain can pose problems associated with ill-conditioned scores caused by power-law decay, recent advances in diffusion-based generative models have shown that transitioning to the wavelet domain offers a promising alternative. However, within the wavelet domain, we encounter unique challenges, especially the sparse representation of high-frequency coefficients, which deviates significantly from the Gaussian assumptions in the diffusion process. To this end, we propose a multi-scale generative modeling in the wavelet domain that employs distinct strategies for handling low and high-frequency bands. In the wavelet domain, we apply score-based generative modeling with well-conditioned scores for low-frequency bands, while utilizing a multi-scale generative adversarial learning for high-frequency bands. As supported by the theoretical analysis and experimental results, our model significantly improve performance and reduce the number of trainable parameters, sampling steps, and time.

Diffusion-based Negative Sampling on Graphs for Link Prediction

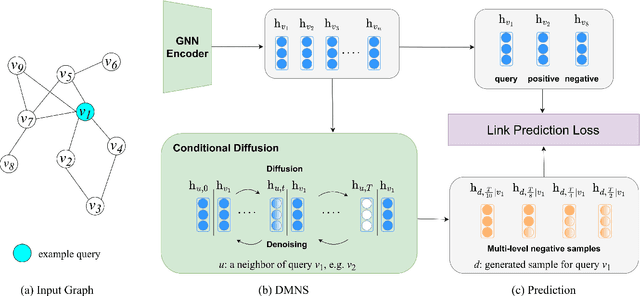
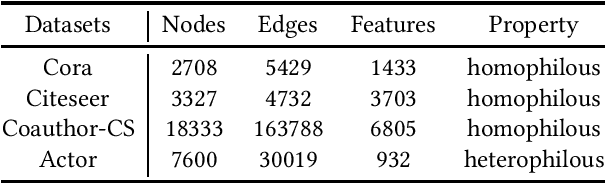
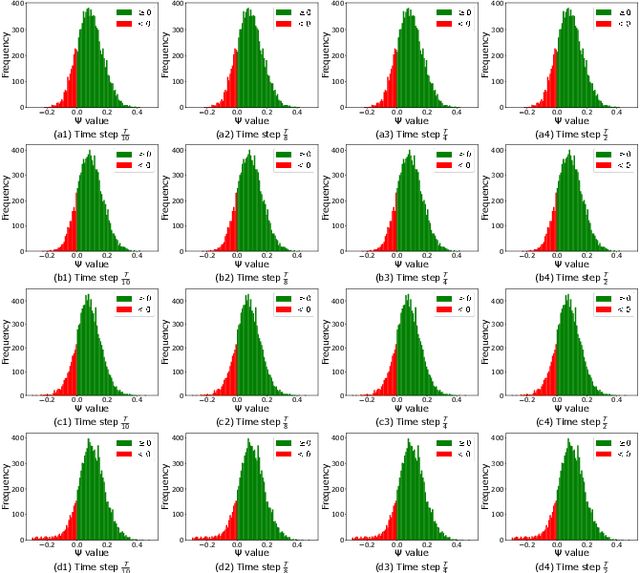
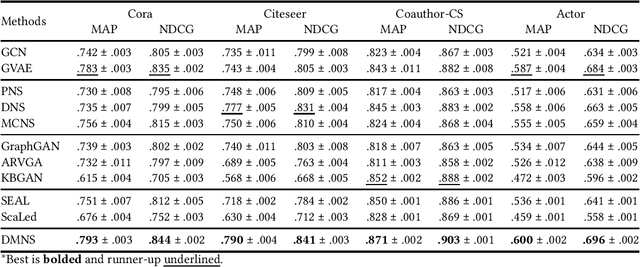
Link prediction is a fundamental task for graph analysis with important applications on the Web, such as social network analysis and recommendation systems, etc. Modern graph link prediction methods often employ a contrastive approach to learn robust node representations, where negative sampling is pivotal. Typical negative sampling methods aim to retrieve hard examples based on either predefined heuristics or automatic adversarial approaches, which might be inflexible or difficult to control. Furthermore, in the context of link prediction, most previous methods sample negative nodes from existing substructures of the graph, missing out on potentially more optimal samples in the latent space. To address these issues, we investigate a novel strategy of multi-level negative sampling that enables negative node generation with flexible and controllable ``hardness'' levels from the latent space. Our method, called Conditional Diffusion-based Multi-level Negative Sampling (DMNS), leverages the Markov chain property of diffusion models to generate negative nodes in multiple levels of variable hardness and reconcile them for effective graph link prediction. We further demonstrate that DMNS follows the sub-linear positivity principle for robust negative sampling. Extensive experiments on several benchmark datasets demonstrate the effectiveness of DMNS.

Link Prediction on Latent Heterogeneous Graphs

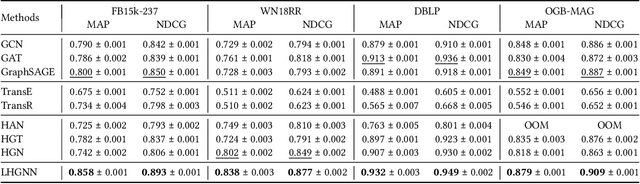
On graph data, the multitude of node or edge types gives rise to heterogeneous information networks (HINs). To preserve the heterogeneous semantics on HINs, the rich node/edge types become a cornerstone of HIN representation learning. However, in real-world scenarios, type information is often noisy, missing or inaccessible. Assuming no type information is given, we define a so-called latent heterogeneous graph (LHG), which carries latent heterogeneous semantics as the node/edge types cannot be observed. In this paper, we study the challenging and unexplored problem of link prediction on an LHG. As existing approaches depend heavily on type-based information, they are suboptimal or even inapplicable on LHGs. To address the absence of type information, we propose a model named LHGNN, based on the novel idea of semantic embedding at node and path levels, to capture latent semantics on and between nodes. We further design a personalization function to modulate the heterogeneous contexts conditioned on their latent semantics w.r.t. the target node, to enable finer-grained aggregation. Finally, we conduct extensive experiments on four benchmark datasets, and demonstrate the superior performance of LHGNN.

On Generalized Degree Fairness in Graph Neural Networks

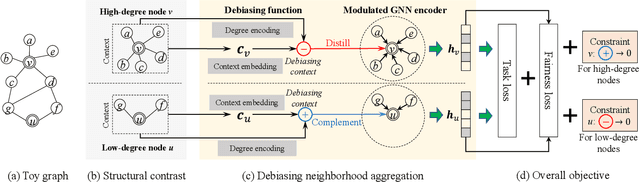
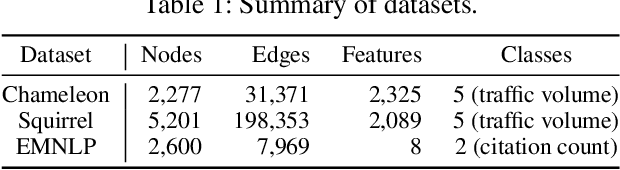
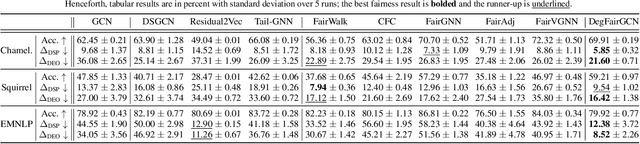
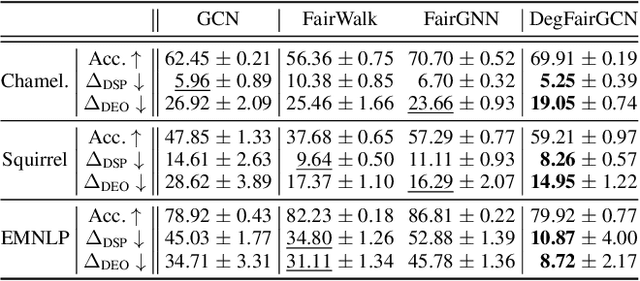
Conventional graph neural networks (GNNs) are often confronted with fairness issues that may stem from their input, including node attributes and neighbors surrounding a node. While several recent approaches have been proposed to eliminate the bias rooted in sensitive attributes, they ignore the other key input of GNNs, namely the neighbors of a node, which can introduce bias since GNNs hinge on neighborhood structures to generate node representations. In particular, the varying neighborhood structures across nodes, manifesting themselves in drastically different node degrees, give rise to the diverse behaviors of nodes and biased outcomes. In this paper, we first define and generalize the degree bias using a generalized definition of node degree as a manifestation and quantification of different multi-hop structures around different nodes. To address the bias in the context of node classification, we propose a novel GNN framework called Generalized Degree Fairness-centric Graph Neural Network (Deg-FairGNN). Specifically, in each GNN layer, we employ a learnable debiasing function to generate debiasing contexts, which modulate the layer-wise neighborhood aggregation to eliminate the degree bias originating from the diverse degrees among nodes. Extensive experiments on three benchmark datasets demonstrate the effectiveness of our model on both accuracy and fairness metrics.

Towards Good Practices for Data Augmentation in GAN Training

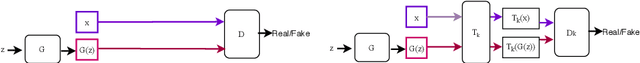
Recent successes in Generative Adversarial Networks (GAN) have affirmed the importance of using more data in GAN training. Yet it is expensive to collect data in many domains such as medical applications. Data Augmentation (DA) has been applied in these applications. In this work, we first argue that the classical DA approach could mislead the generator to learn the distribution of the augmented data, which could be different from that of the original data. We then propose a principled framework, termed Data Augmentation Optimized for GAN (DAG), to enable the use of augmented data in GAN training to improve the learning of the original distribution. We provide theoretical analysis to show that using our proposed DAG aligns with the original GAN in minimizing the JS divergence w.r.t. the original distribution and it leverages the augmented data to improve the learnings of discriminator and generator. The experiments show that DAG improves various GAN models. Furthermore, when DAG is used in some GAN models, the system establishes state-of-the-art Fr\'echet Inception Distance (FID) scores.