MM-Path: Multi-modal, Multi-granularity Path Representation Learning -- Extended Version

Developing effective path representations has become increasingly essential across various fields within intelligent transportation. Although pre-trained path representation learning models have shown improved performance, they predominantly focus on the topological structures from single modality data, i.e., road networks, overlooking the geometric and contextual features associated with path-related images, e.g., remote sensing images. Similar to human understanding, integrating information from multiple modalities can provide a more comprehensive view, enhancing both representation accuracy and generalization. However, variations in information granularity impede the semantic alignment of road network-based paths (road paths) and image-based paths (image paths), while the heterogeneity of multi-modal data poses substantial challenges for effective fusion and utilization. In this paper, we propose a novel Multi-modal, Multi-granularity Path Representation Learning Framework (MM-Path), which can learn a generic path representation by integrating modalities from both road paths and image paths. To enhance the alignment of multi-modal data, we develop a multi-granularity alignment strategy that systematically associates nodes, road sub-paths, and road paths with their corresponding image patches, ensuring the synchronization of both detailed local information and broader global contexts. To address the heterogeneity of multi-modal data effectively, we introduce a graph-based cross-modal residual fusion component designed to comprehensively fuse information across different modalities and granularities. Finally, we conduct extensive experiments on two large-scale real-world datasets under two downstream tasks, validating the effectiveness of the proposed MM-Path. The code is available at: https://github.com/decisionintelligence/MM-Path.

Air Quality Prediction with Physics-Informed Dual Neural ODEs in Open Systems

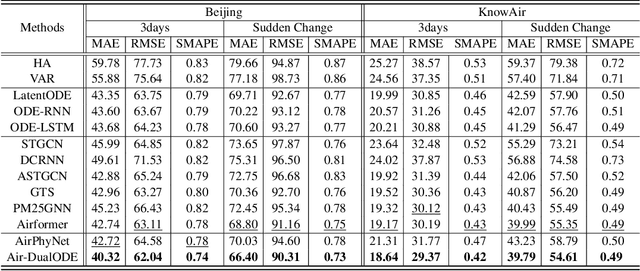
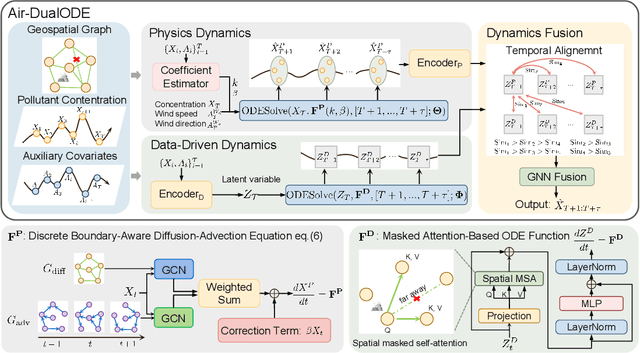
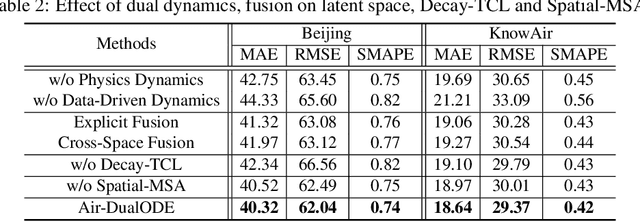
Air pollution significantly threatens human health and ecosystems, necessitating effective air quality prediction to inform public policy. Traditional approaches are generally categorized into physics-based and data-driven models. Physics-based models usually struggle with high computational demands and closed-system assumptions, while data-driven models may overlook essential physical dynamics, confusing the capturing of spatiotemporal correlations. Although some physics-informed approaches combine the strengths of both models, they often face a mismatch between explicit physical equations and implicit learned representations. To address these challenges, we propose Air-DualODE, a novel physics-informed approach that integrates dual branches of Neural ODEs for air quality prediction. The first branch applies open-system physical equations to capture spatiotemporal dependencies for learning physics dynamics, while the second branch identifies the dependencies not addressed by the first in a fully data-driven way. These dual representations are temporally aligned and fused to enhance prediction accuracy. Our experimental results demonstrate that Air-DualODE achieves state-of-the-art performance in predicting pollutant concentrations across various spatial scales, thereby offering a promising solution for real-world air quality challenges.

DiffImp: Efficient Diffusion Model for Probabilistic Time Series Imputation with Bidirectional Mamba Backbone

Probabilistic time series imputation has been widely applied in real-world scenarios due to its ability to estimate uncertainty of imputation results. Meanwhile, denoising diffusion probabilistic models (DDPMs) have achieved great success in probabilistic time series imputation tasks with its power to model complex distributions. However, current DDPM-based probabilistic time series imputation methodologies are confronted with two types of challenges: 1)~\textit{~The backbone modules of the denoising parts are not capable of achieving sequence modeling with low time complexity.} 2)~\textit{The architecture of denoising modules can not handle the inter-variable and bidirectional dependencies in the time series imputation problem effectively.} To address the first challenge, we integrate the computational efficient state space model, namely Mamba, as the backbone denosing module for DDPMs. To tackle the second challenge, we carefully devise several SSM-based blocks for bidirectional modeling and inter-variable relation understanding. Experimental results demonstrate that our approach can achieve state-of-the-art time series imputation results on multiple datasets, different missing scenarios and missing ratios.

Orca: Ocean Significant Wave Height Estimation with Spatio-temporally Aware Large Language Models

Significant wave height (SWH) is a vital metric in marine science, and accurate SWH estimation is crucial for various applications, e.g., marine energy development, fishery, early warning systems for potential risks, etc. Traditional SWH estimation methods that are based on numerical models and physical theories are hindered by computational inefficiencies. Recently, machine learning has emerged as an appealing alternative to improve accuracy and reduce computational time. However, due to limited observational technology and high costs, the scarcity of real-world data restricts the potential of machine learning models. To overcome these limitations, we propose an ocean SWH estimation framework, namely Orca. Specifically, Orca enhances the limited spatio-temporal reasoning abilities of classic LLMs with a novel spatiotemporal aware encoding module. By segmenting the limited buoy observational data temporally, encoding the buoys' locations spatially, and designing prompt templates, Orca capitalizes on the robust generalization ability of LLMs to estimate significant wave height effectively with limited data. Experimental results on the Gulf of Mexico demonstrate that Orca achieves state-of-the-art performance in SWH estimation.

PeFAD: A Parameter-Efficient Federated Framework for Time Series Anomaly Detection

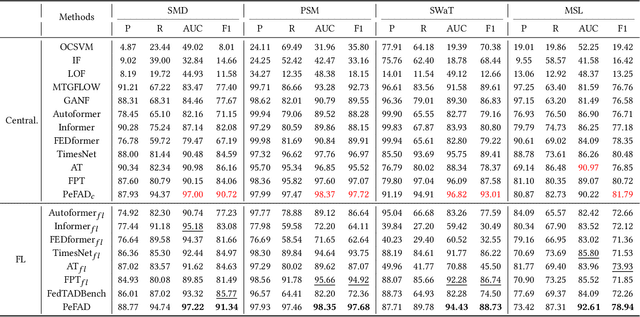
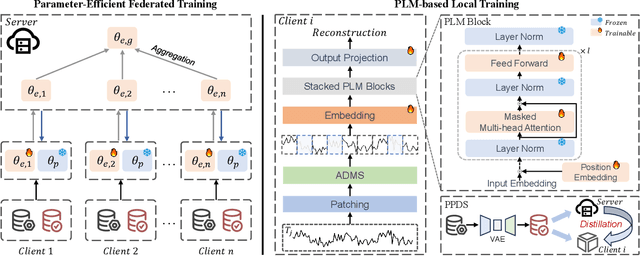
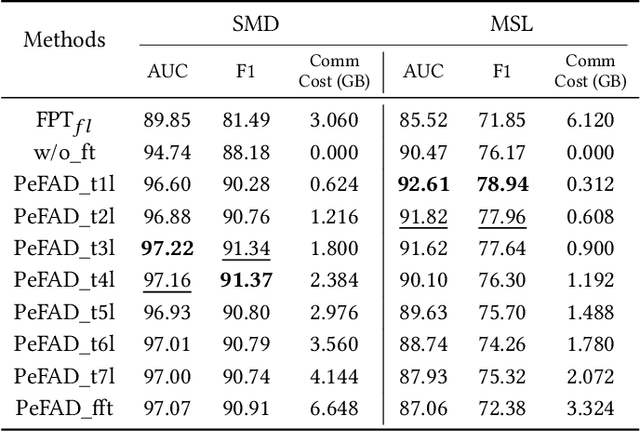
With the proliferation of mobile sensing techniques, huge amounts of time series data are generated and accumulated in various domains, fueling plenty of real-world applications. In this setting, time series anomaly detection is practically important. It endeavors to identify deviant samples from the normal sample distribution in time series. Existing approaches generally assume that all the time series is available at a central location. However, we are witnessing the decentralized collection of time series due to the deployment of various edge devices. To bridge the gap between the decentralized time series data and the centralized anomaly detection algorithms, we propose a Parameter-efficient Federated Anomaly Detection framework named PeFAD with the increasing privacy concerns. PeFAD for the first time employs the pre-trained language model (PLM) as the body of the client's local model, which can benefit from its cross-modality knowledge transfer capability. To reduce the communication overhead and local model adaptation cost, we propose a parameter-efficient federated training module such that clients only need to fine-tune small-scale parameters and transmit them to the server for update. PeFAD utilizes a novel anomaly-driven mask selection strategy to mitigate the impact of neglected anomalies during training. A knowledge distillation operation on a synthetic privacy-preserving dataset that is shared by all the clients is also proposed to address the data heterogeneity issue across clients. We conduct extensive evaluations on four real datasets, where PeFAD outperforms existing state-of-the-art baselines by up to 28.74\%.

Estimating Treatment Effect under Additive Hazards Models with High-dimensional Covariates

Estimating causal effects for survival outcomes in the high-dimensional setting is an extremely important topic for many biomedical applications as well as areas of social sciences. We propose a new orthogonal score method for treatment effect estimation and inference that results in asymptotically valid confidence intervals assuming only good estimation properties of the hazard outcome model and the conditional probability of treatment. This guarantee allows us to provide valid inference for the conditional treatment effect under the high-dimensional additive hazards model under considerably more generality than existing approaches. In addition, we develop a new Hazards Difference (HDi), estimator. We showcase that our approach has double-robustness properties in high dimensions: with cross-fitting, the HDi estimate is consistent under a wide variety of treatment assignment models; the HDi estimate is also consistent when the hazards model is misspecified and instead the true data generating mechanism follows a partially linear additive hazards model. We further develop a novel sparsity doubly robust result, where either the outcome or the treatment model can be a fully dense high-dimensional model. We apply our methods to study the treatment effect of radical prostatectomy versus conservative management for prostate cancer patients using the SEER-Medicare Linked Data.

Fine-Gray competing risks model with high-dimensional covariates: estimation and Inference

The purpose of this paper is to construct confidence intervals for the regression coefficients in the Fine-Gray model for competing risks data with random censoring, where the number of covariates can be larger than the sample size. Despite strong motivation from biostatistics applications, high-dimensional Fine-Gray model has attracted relatively little attention among the methodological or theoretical literatures. We fill in this blank by proposing first a consistent regularized estimator and then the confidence intervals based on the one-step bias-correcting estimator. We are able to generalize the partial likelihood approach for the Fine-Gray model under random censoring despite many technical difficulties. We lay down a methodological and theoretical framework for the one-step bias-correcting estimator with the partial likelihood, which does not have independent and identically distributed entries. We also handle for our theory the approximation error from the inverse probability weighting (IPW), proposing novel concentration results for time dependent processes. In addition to the theoretical results and algorithms, we present extensive numerical experiments and an application to a study of non-cancer mortality among prostate cancer patients using the linked Medicare-SEER data.