Hidden Flaws Behind Expert-Level Accuracy of GPT-4 Vision in Medicine

Recent studies indicate that Generative Pre-trained Transformer 4 with Vision (GPT-4V) outperforms human physicians in medical challenge tasks. However, these evaluations primarily focused on the accuracy of multi-choice questions alone. Our study extends the current scope by conducting a comprehensive analysis of GPT-4V's rationales of image comprehension, recall of medical knowledge, and step-by-step multimodal reasoning when solving New England Journal of Medicine (NEJM) Image Challenges - an imaging quiz designed to test the knowledge and diagnostic capabilities of medical professionals. Evaluation results confirmed that GPT-4V outperforms human physicians regarding multi-choice accuracy (88.0% vs. 77.0%, p=0.034). GPT-4V also performs well in cases where physicians incorrectly answer, with over 80% accuracy. However, we discovered that GPT-4V frequently presents flawed rationales in cases where it makes the correct final choices (27.3%), most prominent in image comprehension (21.6%). Regardless of GPT-4V's high accuracy in multi-choice questions, our findings emphasize the necessity for further in-depth evaluations of its rationales before integrating such models into clinical workflows.

Robust Optimization for Non-Convex Objectives

We consider robust optimization problems, where the goal is to optimize in the worst case over a class of objective functions. We develop a reduction from robust improper optimization to Bayesian optimization: given an oracle that returns $\alpha$-approximate solutions for distributions over objectives, we compute a distribution over solutions that is $\alpha$-approximate in the worst case. We show that de-randomizing this solution is NP-hard in general, but can be done for a broad class of statistical learning tasks. We apply our results to robust neural network training and submodular optimization. We evaluate our approach experimentally on corrupted character classification, and robust influence maximization in networks.

Causal Regularization

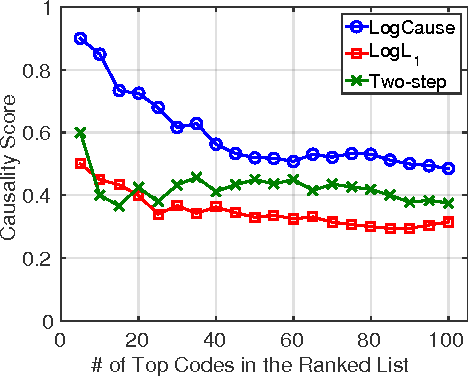
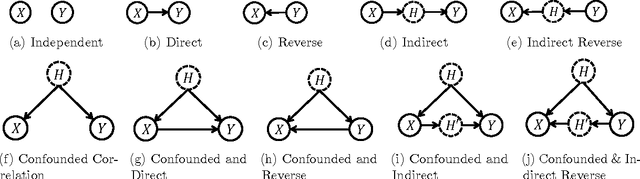
In application domains such as healthcare, we want accurate predictive models that are also causally interpretable. In pursuit of such models, we propose a causal regularizer to steer predictive models towards causally-interpretable solutions and theoretically study its properties. In a large-scale analysis of Electronic Health Records (EHR), our causally-regularized model outperforms its L1-regularized counterpart in causal accuracy and is competitive in predictive performance. We perform non-linear causality analysis by causally regularizing a special neural network architecture. We also show that the proposed causal regularizer can be used together with neural representation learning algorithms to yield up to 20% improvement over multilayer perceptron in detecting multivariate causation, a situation common in healthcare, where many causal factors should occur simultaneously to have an effect on the target variable.

Sparse Hierarchical Tucker Factorization and its Application to Healthcare

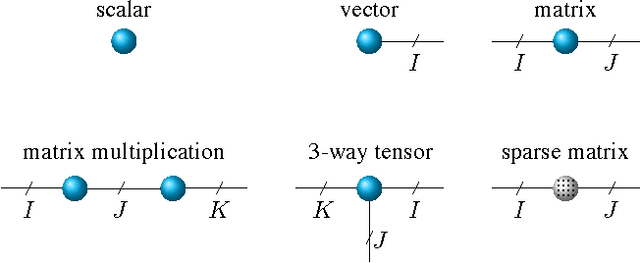
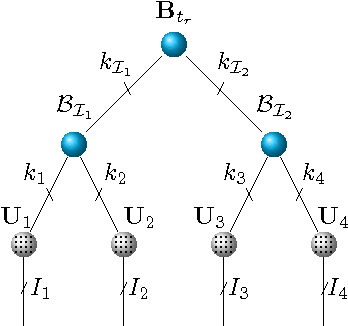
We propose a new tensor factorization method, called the Sparse Hierarchical-Tucker (Sparse H-Tucker), for sparse and high-order data tensors. Sparse H-Tucker is inspired by its namesake, the classical Hierarchical Tucker method, which aims to compute a tree-structured factorization of an input data set that may be readily interpreted by a domain expert. However, Sparse H-Tucker uses a nested sampling technique to overcome a key scalability problem in Hierarchical Tucker, which is the creation of an unwieldy intermediate dense core tensor; the result of our approach is a faster, more space-efficient, and more accurate method. We extensively test our method on a real healthcare dataset, which is collected from 30K patients and results in an 18th order sparse data tensor. Unlike competing methods, Sparse H-Tucker can analyze the full data set on a single multi-threaded machine. It can also do so more accurately and in less time than the state-of-the-art: on a 12th order subset of the input data, Sparse H-Tucker is 18x more accurate and 7.5x faster than a previously state-of-the-art method. Even for analyzing low order tensors (e.g., 4-order), our method requires close to an order of magnitude less time and over two orders of magnitude less memory, as compared to traditional tensor factorization methods such as CP and Tucker. Moreover, we observe that Sparse H-Tucker scales nearly linearly in the number of non-zero tensor elements. The resulting model also provides an interpretable disease hierarchy, which is confirmed by a clinical expert.

Scalable Latent Tree Model and its Application to Health Analytics

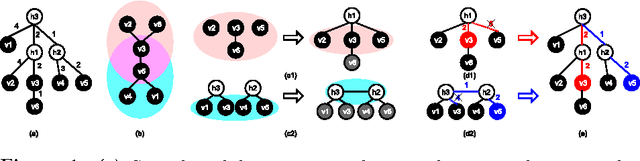
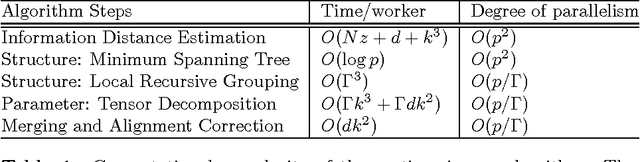
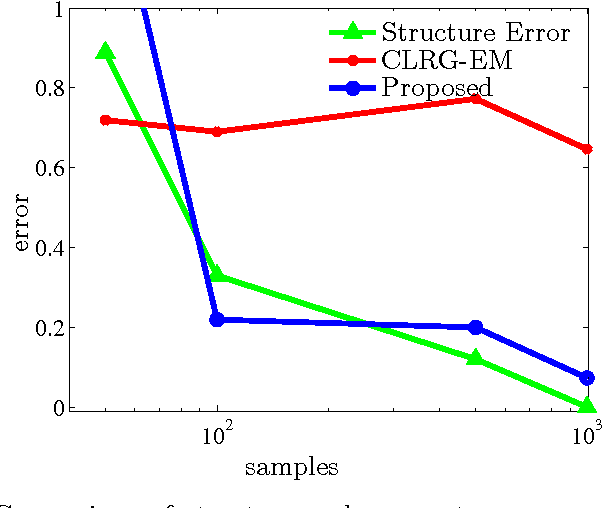
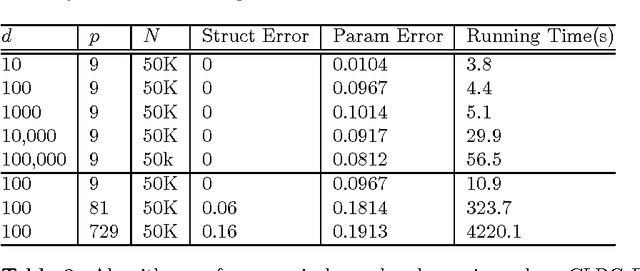
We present an integrated approach to structure and parameter estimation in latent tree graphical models, where some nodes are hidden. Our overall approach follows a "divide-and-conquer" strategy that learns models over small groups of variables and iteratively merges into a global solution. The structure learning involves combinatorial operations such as minimum spanning tree construction and local recursive grouping; the parameter learning is based on the method of moments and on tensor decompositions. Our method is guaranteed to correctly recover the unknown tree structure and the model parameters with low sample complexity for the class of linear multivariate latent tree models which includes discrete and Gaussian distributions, and Gaussian mixtures. Our bulk asynchronous parallel algorithm is implemented in parallel using the OpenMP framework and scales logarithmically with the number of variables and linearly with dimensionality of each variable. Our experiments confirm a high degree of efficiency and accuracy on large datasets of electronic health records. The proposed algorithm also generates intuitive and clinically meaningful disease hierarchies.