Nimble GNN Embedding with Tensor-Train Decomposition

This paper describes a new method for representing embedding tables of graph neural networks (GNNs) more compactly via tensor-train (TT) decomposition. We consider the scenario where (a) the graph data that lack node features, thereby requiring the learning of embeddings during training; and (b) we wish to exploit GPU platforms, where smaller tables are needed to reduce host-to-GPU communication even for large-memory GPUs. The use of TT enables a compact parameterization of the embedding, rendering it small enough to fit entirely on modern GPUs even for massive graphs. When combined with judicious schemes for initialization and hierarchical graph partitioning, this approach can reduce the size of node embedding vectors by 1,659 times to 81,362 times on large publicly available benchmark datasets, achieving comparable or better accuracy and significant speedups on multi-GPU systems. In some cases, our model without explicit node features on input can even match the accuracy of models that use node features.

CUP: Cluster Pruning for Compressing Deep Neural Networks

We propose Cluster Pruning (CUP) for compressing and accelerating deep neural networks. Our approach prunes similar filters by clustering them based on features derived from both the incoming and outgoing weight connections. With CUP, we overcome two limitations of prior work-(1) non-uniform pruning: CUP can efficiently determine the ideal number of filters to prune in each layer of a neural network. This is in contrast to prior methods that either prune all layers uniformly or otherwise use resource-intensive methods such as manual sensitivity analysis or reinforcement learning to determine the ideal number. (2) Single-shot operation: We extend CUP to CUP-SS (for CUP single shot) whereby pruning is integrated into the initial training phase itself. This leads to large savings in training time compared to traditional pruning pipelines. Through extensive evaluation on multiple datasets (MNIST, CIFAR-10, and Imagenet) and models(VGG-16, Resnets-18/34/56) we show that CUP outperforms recent state of the art. Specifically, CUP-SS achieves 2.2x flops reduction for a Resnet-50 model trained on Imagenet while staying within 0.9% top-5 accuracy. It saves over 14 hours in training time with respect to the original Resnet-50. The code to reproduce results is available.

SUSTain: Scalable Unsupervised Scoring for Tensors and its Application to Phenotyping

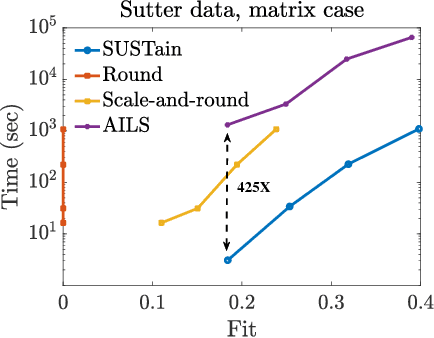
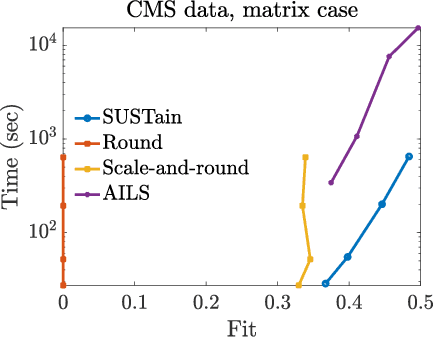
This paper presents a new method, which we call SUSTain, that extends real-valued matrix and tensor factorizations to data where values are integers. Such data are common when the values correspond to event counts or ordinal measures. The conventional approach is to treat integer data as real, and then apply real-valued factorizations. However, doing so fails to preserve important characteristics of the original data, thereby making it hard to interpret the results. Instead, our approach extracts factor values from integer datasets as scores that are constrained to take values from a small integer set. These scores are easy to interpret: a score of zero indicates no feature contribution and higher scores indicate distinct levels of feature importance. At its core, SUSTain relies on: a) a problem partitioning into integer-constrained subproblems, so that they can be optimally solved in an efficient manner; and b) organizing the order of the subproblems' solution, to promote reuse of shared intermediate results. We propose two variants, SUSTain_M and SUSTain_T, to handle both matrix and tensor inputs, respectively. We evaluate SUSTain against several state-of-the-art baselines on both synthetic and real Electronic Health Record (EHR) datasets. Comparing to those baselines, SUSTain shows either significantly better fit or orders of magnitude speedups that achieve a comparable fit (up to 425X faster). We apply SUSTain to EHR datasets to extract patient phenotypes (i.e., clinically meaningful patient clusters). Furthermore, 87% of them were validated as clinically meaningful phenotypes related to heart failure by a cardiologist.

SPARTan: Scalable PARAFAC2 for Large & Sparse Data

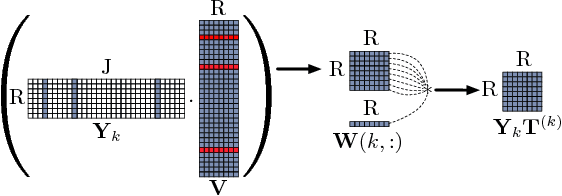
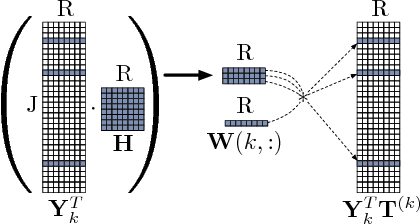
In exploratory tensor mining, a common problem is how to analyze a set of variables across a set of subjects whose observations do not align naturally. For example, when modeling medical features across a set of patients, the number and duration of treatments may vary widely in time, meaning there is no meaningful way to align their clinical records across time points for analysis purposes. To handle such data, the state-of-the-art tensor model is the so-called PARAFAC2, which yields interpretable and robust output and can naturally handle sparse data. However, its main limitation up to now has been the lack of efficient algorithms that can handle large-scale datasets. In this work, we fill this gap by developing a scalable method to compute the PARAFAC2 decomposition of large and sparse datasets, called SPARTan. Our method exploits special structure within PARAFAC2, leading to a novel algorithmic reformulation that is both fast (in absolute time) and more memory-efficient than prior work. We evaluate SPARTan on both synthetic and real datasets, showing 22X performance gains over the best previous implementation and also handling larger problem instances for which the baseline fails. Furthermore, we are able to apply SPARTan to the mining of temporally-evolving phenotypes on data taken from real and medically complex pediatric patients. The clinical meaningfulness of the phenotypes identified in this process, as well as their temporal evolution over time for several patients, have been endorsed by clinical experts.

Sparse Hierarchical Tucker Factorization and its Application to Healthcare

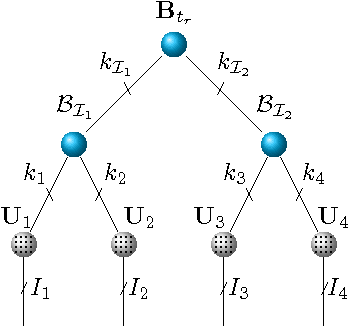
We propose a new tensor factorization method, called the Sparse Hierarchical-Tucker (Sparse H-Tucker), for sparse and high-order data tensors. Sparse H-Tucker is inspired by its namesake, the classical Hierarchical Tucker method, which aims to compute a tree-structured factorization of an input data set that may be readily interpreted by a domain expert. However, Sparse H-Tucker uses a nested sampling technique to overcome a key scalability problem in Hierarchical Tucker, which is the creation of an unwieldy intermediate dense core tensor; the result of our approach is a faster, more space-efficient, and more accurate method. We extensively test our method on a real healthcare dataset, which is collected from 30K patients and results in an 18th order sparse data tensor. Unlike competing methods, Sparse H-Tucker can analyze the full data set on a single multi-threaded machine. It can also do so more accurately and in less time than the state-of-the-art: on a 12th order subset of the input data, Sparse H-Tucker is 18x more accurate and 7.5x faster than a previously state-of-the-art method. Even for analyzing low order tensors (e.g., 4-order), our method requires close to an order of magnitude less time and over two orders of magnitude less memory, as compared to traditional tensor factorization methods such as CP and Tucker. Moreover, we observe that Sparse H-Tucker scales nearly linearly in the number of non-zero tensor elements. The resulting model also provides an interpretable disease hierarchy, which is confirmed by a clinical expert.