TASTE: Temporal and Static Tensor Factorization for Phenotyping Electronic Health Records

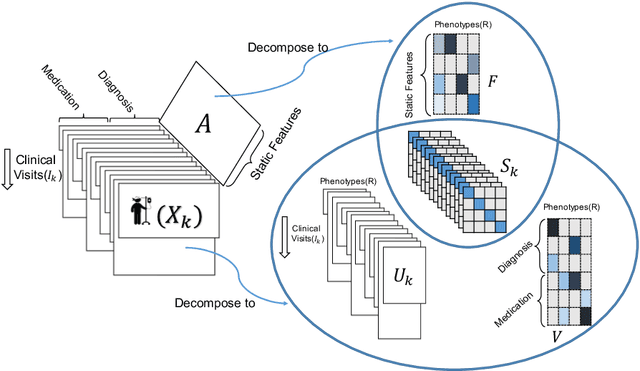
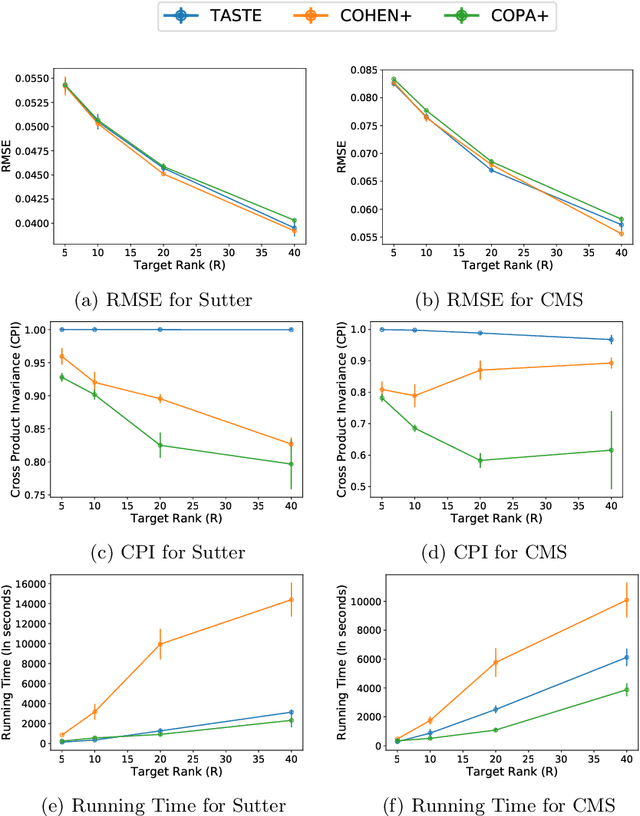
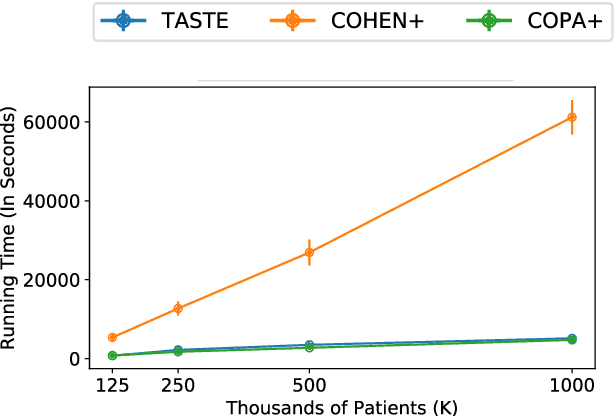
Phenotyping electronic health records (EHR) focuses on defining meaningful patient groups (e.g., heart failure group and diabetes group) and identifying the temporal evolution of patients in those groups. Tensor factorization has been an effective tool for phenotyping. Most of the existing works assume either a static patient representation with aggregate data or only model temporal data. However, real EHR data contain both temporal (e.g., longitudinal clinical visits) and static information (e.g., patient demographics), which are difficult to model simultaneously. In this paper, we propose Temporal And Static TEnsor factorization (TASTE) that jointly models both static and temporal information to extract phenotypes. TASTE combines the PARAFAC2 model with non-negative matrix factorization to model a temporal and a static tensor. To fit the proposed model, we transform the original problem into simpler ones which are optimally solved in an alternating fashion. For each of the sub-problems, our proposed mathematical reformulations lead to efficient sub-problem solvers. Comprehensive experiments on large EHR data from a heart failure (HF) study confirmed that TASTE is up to 14x faster than several baselines and the resulting phenotypes were confirmed to be clinically meaningful by a cardiologist. Using 80 phenotypes extracted by TASTE, a simple logistic regression can achieve the same level of area under the curve (AUC) for HF prediction compared to a deep learning model using recurrent neural networks (RNN) with 345 features.

SUSTain: Scalable Unsupervised Scoring for Tensors and its Application to Phenotyping

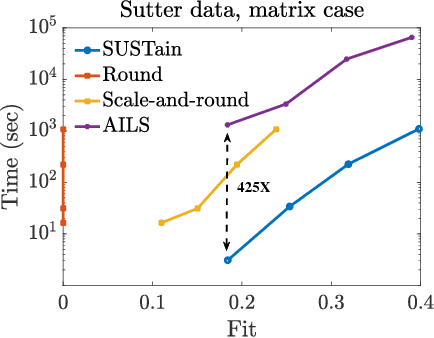
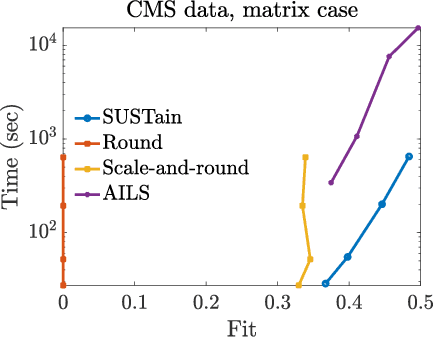
This paper presents a new method, which we call SUSTain, that extends real-valued matrix and tensor factorizations to data where values are integers. Such data are common when the values correspond to event counts or ordinal measures. The conventional approach is to treat integer data as real, and then apply real-valued factorizations. However, doing so fails to preserve important characteristics of the original data, thereby making it hard to interpret the results. Instead, our approach extracts factor values from integer datasets as scores that are constrained to take values from a small integer set. These scores are easy to interpret: a score of zero indicates no feature contribution and higher scores indicate distinct levels of feature importance. At its core, SUSTain relies on: a) a problem partitioning into integer-constrained subproblems, so that they can be optimally solved in an efficient manner; and b) organizing the order of the subproblems' solution, to promote reuse of shared intermediate results. We propose two variants, SUSTain_M and SUSTain_T, to handle both matrix and tensor inputs, respectively. We evaluate SUSTain against several state-of-the-art baselines on both synthetic and real Electronic Health Record (EHR) datasets. Comparing to those baselines, SUSTain shows either significantly better fit or orders of magnitude speedups that achieve a comparable fit (up to 425X faster). We apply SUSTain to EHR datasets to extract patient phenotypes (i.e., clinically meaningful patient clusters). Furthermore, 87% of them were validated as clinically meaningful phenotypes related to heart failure by a cardiologist.

Solving a New 3D Bin Packing Problem with Deep Reinforcement Learning Method

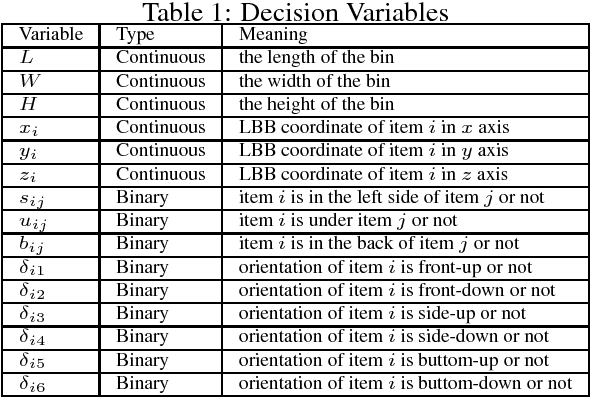
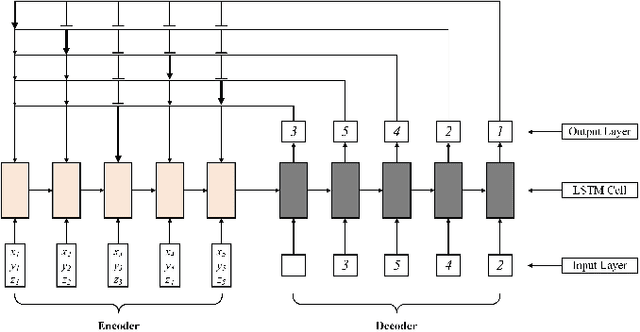
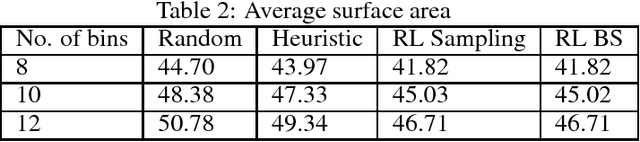
In this paper, a new type of 3D bin packing problem (BPP) is proposed, in which a number of cuboid-shaped items must be put into a bin one by one orthogonally. The objective is to find a way to place these items that can minimize the surface area of the bin. This problem is based on the fact that there is no fixed-sized bin in many real business scenarios and the cost of a bin is proportional to its surface area. Our research shows that this problem is NP-hard. Based on previous research on 3D BPP, the surface area is determined by the sequence, spatial locations and orientations of items. Among these factors, the sequence of items plays a key role in minimizing the surface area. Inspired by recent achievements of deep reinforcement learning (DRL) techniques, especially Pointer Network, on combinatorial optimization problems such as TSP, a DRL-based method is applied to optimize the sequence of items to be packed into the bin. Numerical results show that the method proposed in this paper achieve about 5% improvement than heuristic method.