TASTE: Temporal and Static Tensor Factorization for Phenotyping Electronic Health Records

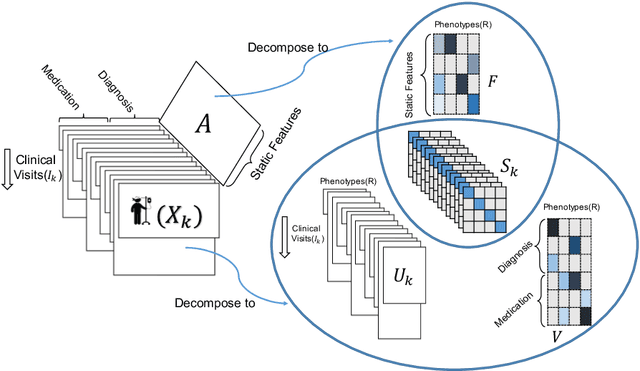
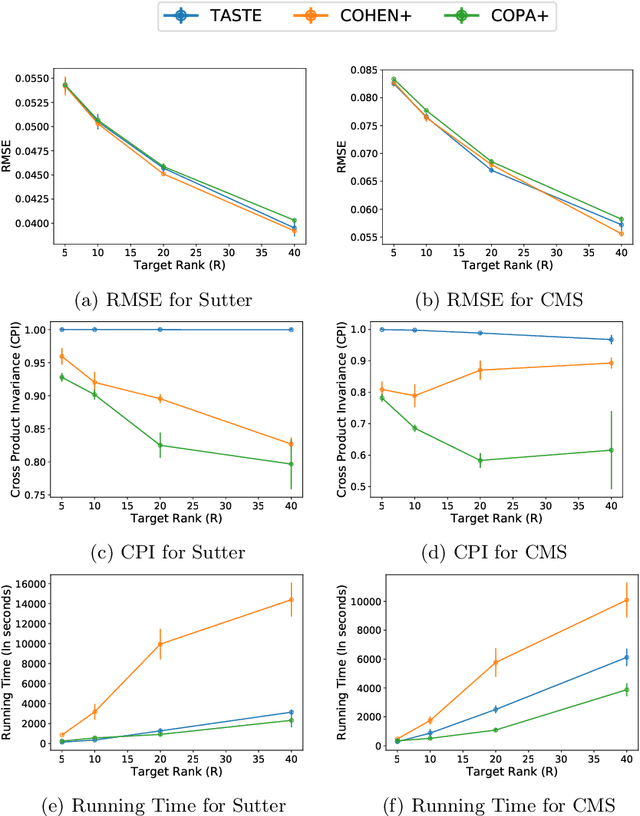
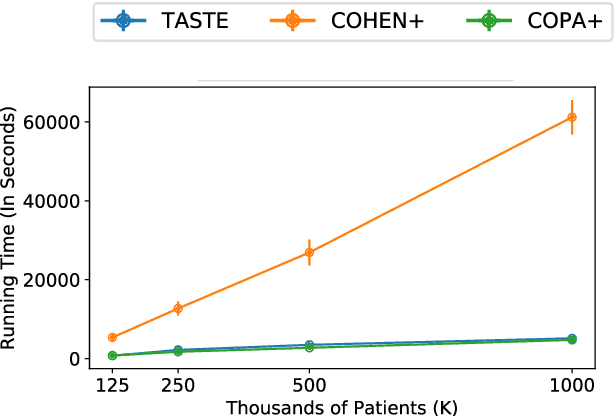
Phenotyping electronic health records (EHR) focuses on defining meaningful patient groups (e.g., heart failure group and diabetes group) and identifying the temporal evolution of patients in those groups. Tensor factorization has been an effective tool for phenotyping. Most of the existing works assume either a static patient representation with aggregate data or only model temporal data. However, real EHR data contain both temporal (e.g., longitudinal clinical visits) and static information (e.g., patient demographics), which are difficult to model simultaneously. In this paper, we propose Temporal And Static TEnsor factorization (TASTE) that jointly models both static and temporal information to extract phenotypes. TASTE combines the PARAFAC2 model with non-negative matrix factorization to model a temporal and a static tensor. To fit the proposed model, we transform the original problem into simpler ones which are optimally solved in an alternating fashion. For each of the sub-problems, our proposed mathematical reformulations lead to efficient sub-problem solvers. Comprehensive experiments on large EHR data from a heart failure (HF) study confirmed that TASTE is up to 14x faster than several baselines and the resulting phenotypes were confirmed to be clinically meaningful by a cardiologist. Using 80 phenotypes extracted by TASTE, a simple logistic regression can achieve the same level of area under the curve (AUC) for HF prediction compared to a deep learning model using recurrent neural networks (RNN) with 345 features.

COPA: Constrained PARAFAC2 for Sparse & Large Datasets

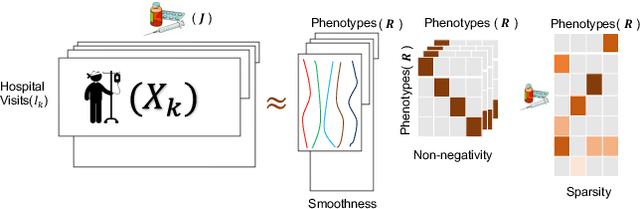
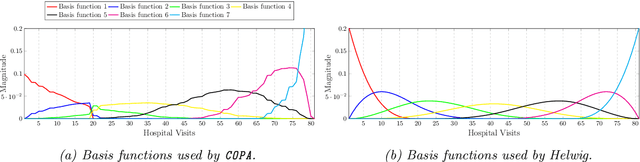
PARAFAC2 has demonstrated success in modeling irregular tensors, where the tensor dimensions vary across one of the modes. An example scenario is modeling treatments across a set of patients with the varying number of medical encounters over time. Despite recent improvements on unconstrained PARAFAC2, its model factors are usually dense and sensitive to noise which limits their interpretability. As a result, the following open challenges remain: a) various modeling constraints, such as temporal smoothness, sparsity and non-negativity, are needed to be imposed for interpretable temporal modeling and b) a scalable approach is required to support those constraints efficiently for large datasets. To tackle these challenges, we propose a {\it CO}nstrained {\it PA}RAFAC2 (COPA) method, which carefully incorporates optimization constraints such as temporal smoothness, sparsity, and non-negativity in the resulting factors. To efficiently support all those constraints, COPA adopts a hybrid optimization framework using alternating optimization and alternating direction method of multiplier (AO-ADMM). As evaluated on large electronic health record (EHR) datasets with hundreds of thousands of patients, COPA achieves significant speedups (up to 36 times faster) over prior PARAFAC2 approaches that only attempt to handle a subset of the constraints that COPA enables. Overall, our method outperforms all the baselines attempting to handle a subset of the constraints in terms of speed, while achieving the same level of accuracy. Through a case study on temporal phenotyping of medically complex children, we demonstrate how the constraints imposed by COPA reveal concise phenotypes and meaningful temporal profiles of patients. The clinical interpretation of both the phenotypes and the temporal profiles was confirmed by a medical expert.

SUSTain: Scalable Unsupervised Scoring for Tensors and its Application to Phenotyping

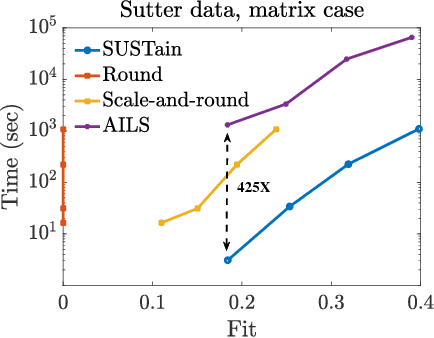
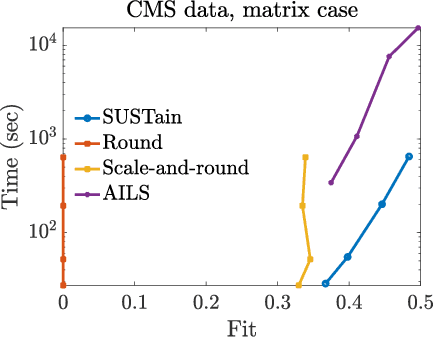
This paper presents a new method, which we call SUSTain, that extends real-valued matrix and tensor factorizations to data where values are integers. Such data are common when the values correspond to event counts or ordinal measures. The conventional approach is to treat integer data as real, and then apply real-valued factorizations. However, doing so fails to preserve important characteristics of the original data, thereby making it hard to interpret the results. Instead, our approach extracts factor values from integer datasets as scores that are constrained to take values from a small integer set. These scores are easy to interpret: a score of zero indicates no feature contribution and higher scores indicate distinct levels of feature importance. At its core, SUSTain relies on: a) a problem partitioning into integer-constrained subproblems, so that they can be optimally solved in an efficient manner; and b) organizing the order of the subproblems' solution, to promote reuse of shared intermediate results. We propose two variants, SUSTain_M and SUSTain_T, to handle both matrix and tensor inputs, respectively. We evaluate SUSTain against several state-of-the-art baselines on both synthetic and real Electronic Health Record (EHR) datasets. Comparing to those baselines, SUSTain shows either significantly better fit or orders of magnitude speedups that achieve a comparable fit (up to 425X faster). We apply SUSTain to EHR datasets to extract patient phenotypes (i.e., clinically meaningful patient clusters). Furthermore, 87% of them were validated as clinically meaningful phenotypes related to heart failure by a cardiologist.

SPARTan: Scalable PARAFAC2 for Large & Sparse Data

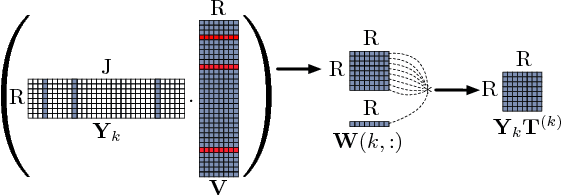
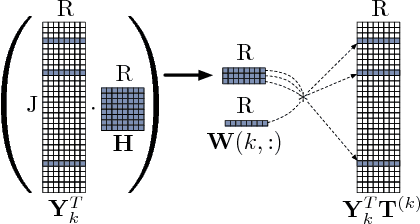
In exploratory tensor mining, a common problem is how to analyze a set of variables across a set of subjects whose observations do not align naturally. For example, when modeling medical features across a set of patients, the number and duration of treatments may vary widely in time, meaning there is no meaningful way to align their clinical records across time points for analysis purposes. To handle such data, the state-of-the-art tensor model is the so-called PARAFAC2, which yields interpretable and robust output and can naturally handle sparse data. However, its main limitation up to now has been the lack of efficient algorithms that can handle large-scale datasets. In this work, we fill this gap by developing a scalable method to compute the PARAFAC2 decomposition of large and sparse datasets, called SPARTan. Our method exploits special structure within PARAFAC2, leading to a novel algorithmic reformulation that is both fast (in absolute time) and more memory-efficient than prior work. We evaluate SPARTan on both synthetic and real datasets, showing 22X performance gains over the best previous implementation and also handling larger problem instances for which the baseline fails. Furthermore, we are able to apply SPARTan to the mining of temporally-evolving phenotypes on data taken from real and medically complex pediatric patients. The clinical meaningfulness of the phenotypes identified in this process, as well as their temporal evolution over time for several patients, have been endorsed by clinical experts.

Sparse Hierarchical Tucker Factorization and its Application to Healthcare

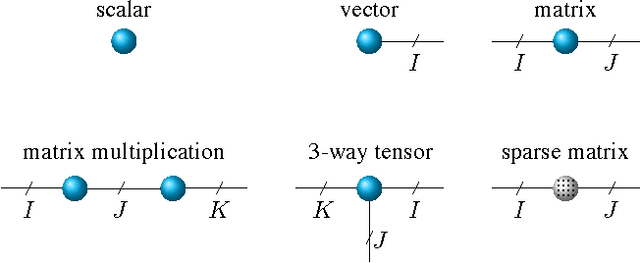
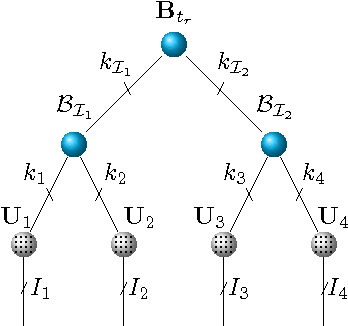
We propose a new tensor factorization method, called the Sparse Hierarchical-Tucker (Sparse H-Tucker), for sparse and high-order data tensors. Sparse H-Tucker is inspired by its namesake, the classical Hierarchical Tucker method, which aims to compute a tree-structured factorization of an input data set that may be readily interpreted by a domain expert. However, Sparse H-Tucker uses a nested sampling technique to overcome a key scalability problem in Hierarchical Tucker, which is the creation of an unwieldy intermediate dense core tensor; the result of our approach is a faster, more space-efficient, and more accurate method. We extensively test our method on a real healthcare dataset, which is collected from 30K patients and results in an 18th order sparse data tensor. Unlike competing methods, Sparse H-Tucker can analyze the full data set on a single multi-threaded machine. It can also do so more accurately and in less time than the state-of-the-art: on a 12th order subset of the input data, Sparse H-Tucker is 18x more accurate and 7.5x faster than a previously state-of-the-art method. Even for analyzing low order tensors (e.g., 4-order), our method requires close to an order of magnitude less time and over two orders of magnitude less memory, as compared to traditional tensor factorization methods such as CP and Tucker. Moreover, we observe that Sparse H-Tucker scales nearly linearly in the number of non-zero tensor elements. The resulting model also provides an interpretable disease hierarchy, which is confirmed by a clinical expert.

Scalable Latent Tree Model and its Application to Health Analytics

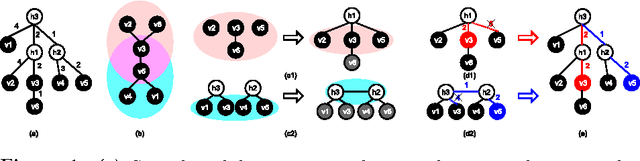
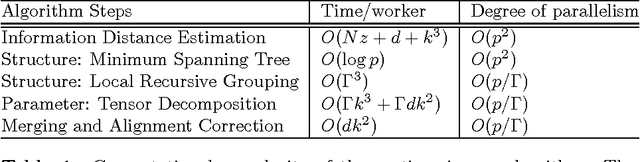
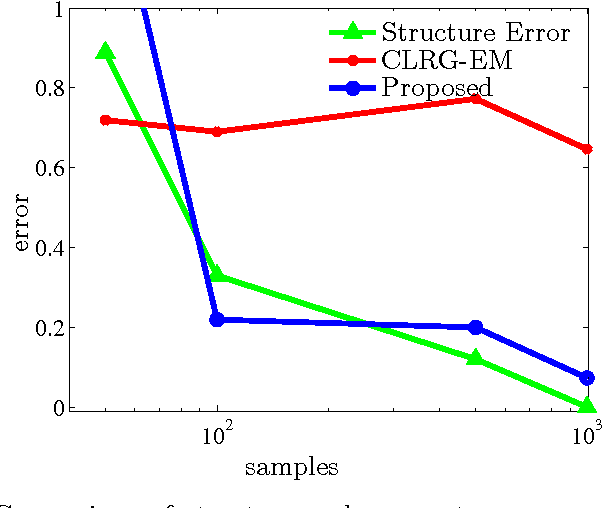
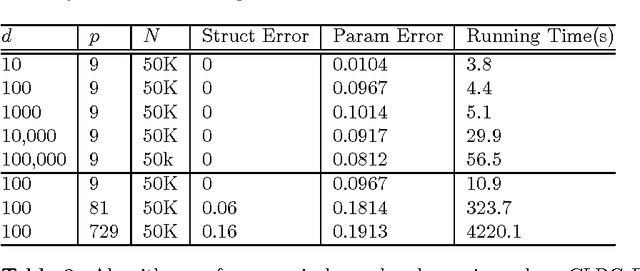
We present an integrated approach to structure and parameter estimation in latent tree graphical models, where some nodes are hidden. Our overall approach follows a "divide-and-conquer" strategy that learns models over small groups of variables and iteratively merges into a global solution. The structure learning involves combinatorial operations such as minimum spanning tree construction and local recursive grouping; the parameter learning is based on the method of moments and on tensor decompositions. Our method is guaranteed to correctly recover the unknown tree structure and the model parameters with low sample complexity for the class of linear multivariate latent tree models which includes discrete and Gaussian distributions, and Gaussian mixtures. Our bulk asynchronous parallel algorithm is implemented in parallel using the OpenMP framework and scales logarithmically with the number of variables and linearly with dimensionality of each variable. Our experiments confirm a high degree of efficiency and accuracy on large datasets of electronic health records. The proposed algorithm also generates intuitive and clinically meaningful disease hierarchies.