Sparse Hierarchical Tucker Factorization and its Application to Healthcare
Paper and Code
Oct 25, 2016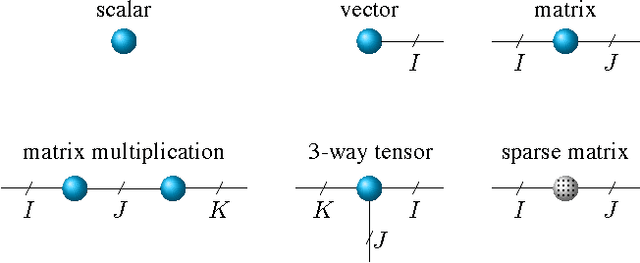

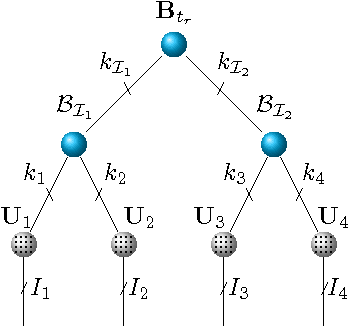

We propose a new tensor factorization method, called the Sparse Hierarchical-Tucker (Sparse H-Tucker), for sparse and high-order data tensors. Sparse H-Tucker is inspired by its namesake, the classical Hierarchical Tucker method, which aims to compute a tree-structured factorization of an input data set that may be readily interpreted by a domain expert. However, Sparse H-Tucker uses a nested sampling technique to overcome a key scalability problem in Hierarchical Tucker, which is the creation of an unwieldy intermediate dense core tensor; the result of our approach is a faster, more space-efficient, and more accurate method. We extensively test our method on a real healthcare dataset, which is collected from 30K patients and results in an 18th order sparse data tensor. Unlike competing methods, Sparse H-Tucker can analyze the full data set on a single multi-threaded machine. It can also do so more accurately and in less time than the state-of-the-art: on a 12th order subset of the input data, Sparse H-Tucker is 18x more accurate and 7.5x faster than a previously state-of-the-art method. Even for analyzing low order tensors (e.g., 4-order), our method requires close to an order of magnitude less time and over two orders of magnitude less memory, as compared to traditional tensor factorization methods such as CP and Tucker. Moreover, we observe that Sparse H-Tucker scales nearly linearly in the number of non-zero tensor elements. The resulting model also provides an interpretable disease hierarchy, which is confirmed by a clinical expert.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge