DRiVE: Diffusion-based Rigging Empowers Generation of Versatile and Expressive Characters

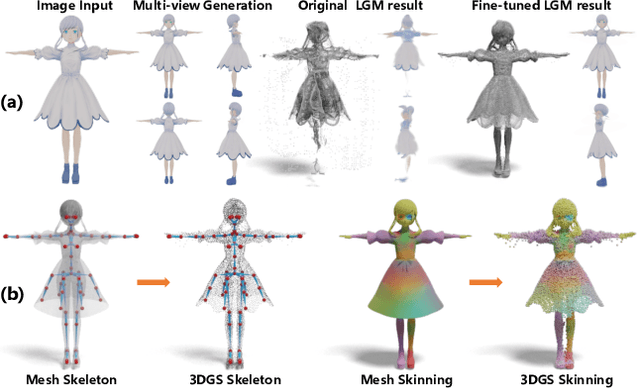
Recent advances in generative models have enabled high-quality 3D character reconstruction from multi-modal. However, animating these generated characters remains a challenging task, especially for complex elements like garments and hair, due to the lack of large-scale datasets and effective rigging methods. To address this gap, we curate AnimeRig, a large-scale dataset with detailed skeleton and skinning annotations. Building upon this, we propose DRiVE, a novel framework for generating and rigging 3D human characters with intricate structures. Unlike existing methods, DRiVE utilizes a 3D Gaussian representation, facilitating efficient animation and high-quality rendering. We further introduce GSDiff, a 3D Gaussian-based diffusion module that predicts joint positions as spatial distributions, overcoming the limitations of regression-based approaches. Extensive experiments demonstrate that DRiVE achieves precise rigging results, enabling realistic dynamics for clothing and hair, and surpassing previous methods in both quality and versatility. The code and dataset will be made public for academic use upon acceptance.

SRIF: Semantic Shape Registration Empowered by Diffusion-based Image Morphing and Flow Estimation

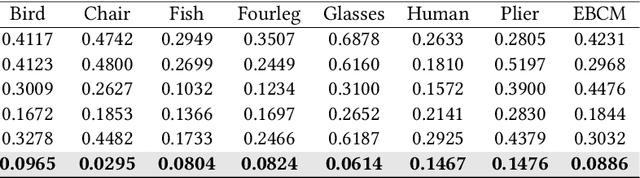
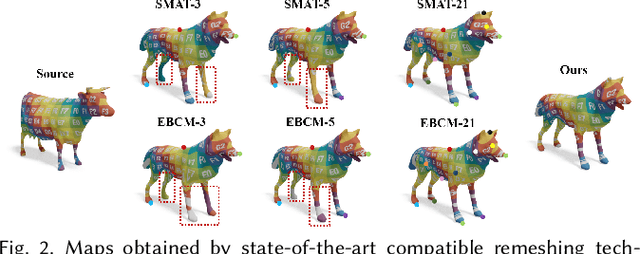
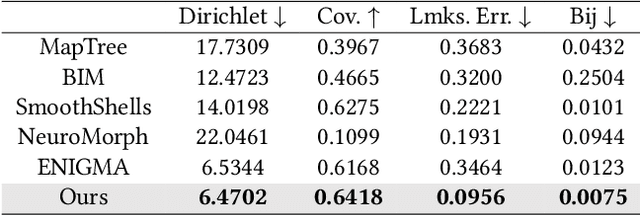
In this paper, we propose SRIF, a novel Semantic shape Registration framework based on diffusion-based Image morphing and Flow estimation. More concretely, given a pair of extrinsically aligned shapes, we first render them from multi-views, and then utilize an image interpolation framework based on diffusion models to generate sequences of intermediate images between them. The images are later fed into a dynamic 3D Gaussian splatting framework, with which we reconstruct and post-process for intermediate point clouds respecting the image morphing processing. In the end, tailored for the above, we propose a novel registration module to estimate continuous normalizing flow, which deforms source shape consistently towards the target, with intermediate point clouds as weak guidance. Our key insight is to leverage large vision models (LVMs) to associate shapes and therefore obtain much richer semantic information on the relationship between shapes than the ad-hoc feature extraction and alignment. As a consequence, SRIF achieves high-quality dense correspondences on challenging shape pairs, but also delivers smooth, semantically meaningful interpolation in between. Empirical evidence justifies the effectiveness and superiority of our method as well as specific design choices. The code is released at https://github.com/rqhuang88/SRIF.

Unsupervised Non-Rigid Point Cloud Matching through Large Vision Models

In this paper, we propose a novel learning-based framework for non-rigid point cloud matching, which can be trained purely on point clouds without any correspondence annotation but also be extended naturally to partial-to-full matching. Our key insight is to incorporate semantic features derived from large vision models (LVMs) to geometry-based shape feature learning. Our framework effectively leverages the structural information contained in the semantic features to address ambiguities arise from self-similarities among local geometries. Furthermore, our framework also enjoys the strong generalizability and robustness regarding partial observations of LVMs, leading to improvements in the regarding point cloud matching tasks. In order to achieve the above, we propose a pixel-to-point feature aggregation module, a local and global attention network as well as a geometrical similarity loss function. Experimental results show that our method achieves state-of-the-art results in matching non-rigid point clouds in both near-isometric and heterogeneous shape collection as well as more realistic partial and noisy data.

Non-Rigid Shape Registration via Deep Functional Maps Prior

In this paper, we propose a learning-based framework for non-rigid shape registration without correspondence supervision. Traditional shape registration techniques typically rely on correspondences induced by extrinsic proximity, therefore can fail in the presence of large intrinsic deformations. Spectral mapping methods overcome this challenge by embedding shapes into, geometric or learned, high-dimensional spaces, where shapes are easier to align. However, due to the dependency on abstract, non-linear embedding schemes, the latter can be vulnerable with respect to perturbed or alien input. In light of this, our framework takes the best of both worlds. Namely, we deform source mesh towards the target point cloud, guided by correspondences induced by high-dimensional embeddings learned from deep functional maps (DFM). In particular, the correspondences are dynamically updated according to the intermediate registrations and filtered by consistency prior, which prominently robustify the overall pipeline. Moreover, in order to alleviate the requirement of extrinsically aligned input, we train an orientation regressor on a set of aligned synthetic shapes independent of the training shapes for DFM. Empirical results show that, with as few as dozens of training shapes of limited variability, our pipeline achieves state-of-the-art results on several benchmarks of non-rigid point cloud matching, but also delivers high-quality correspondences between unseen challenging shape pairs that undergo both significant extrinsic and intrinsic deformations, in which case neither traditional registration methods nor intrinsic methods work. The code is available at https://github.com/rqhuang88/DFR.

Spatially and Spectrally Consistent Deep Functional Maps

Cycle consistency has long been exploited as a powerful prior for jointly optimizing maps within a collection of shapes. In this paper, we investigate its utility in the approaches of Deep Functional Maps, which are considered state-of-the-art in non-rigid shape matching. We first justify that under certain conditions, the learned maps, when represented in the spectral domain, are already cycle consistent. Furthermore, we identify the discrepancy that spectrally consistent maps are not necessarily spatially, or point-wise, consistent. In light of this, we present a novel design of unsupervised Deep Functional Maps, which effectively enforces the harmony of learned maps under the spectral and the point-wise representation. By taking advantage of cycle consistency, our framework produces state-of-the-art results in mapping shapes even under significant distortions. Beyond that, by independently estimating maps in both spectral and spatial domains, our method naturally alleviates over-fitting in network training, yielding superior generalization performance and accuracy within an array of challenging tests for both near-isometric and non-isometric datasets. Codes are available at https://github.com/rqhuang88/Spatiallyand-Spectrally-Consistent-Deep-Functional-Maps.

Neural Intrinsic Embedding for Non-rigid Point Cloud Matching

As a primitive 3D data representation, point clouds are prevailing in 3D sensing, yet short of intrinsic structural information of the underlying objects. Such discrepancy poses great challenges on directly establishing correspondences between point clouds sampled from deformable shapes. In light of this, we propose Neural Intrinsic Embedding (NIE) to embed each vertex into a high-dimensional space in a way that respects the intrinsic structure. Based upon NIE, we further present a weakly-supervised learning framework for non-rigid point cloud registration. Unlike the prior works, we do not require expansive and sensitive off-line basis construction (e.g., eigen-decomposition of Laplacians), nor do we require ground-truth correspondence labels for supervision. We empirically show that our framework performs on par with or even better than the state-of-the-art baselines, which generally require more supervision and/or more structural geometric input.