Personalized Interpolation: An Efficient Method to Tame Flexible Optimization Window Estimation

In the realm of online advertising, optimizing conversions is crucial for delivering relevant products to users and enhancing business outcomes. Predicting conversion events is challenging due to variable delays between user interactions, such as impressions or clicks, and the actual conversions. These delays differ significantly across various advertisers and products, necessitating distinct optimization time windows for targeted conversions. To address this, we introduce a novel approach named the \textit{Personalized Interpolation} method, which innovatively builds upon existing fixed conversion window models to estimate flexible conversion windows. This method allows for the accurate estimation of conversions across a variety of delay ranges, thus meeting the diverse needs of advertisers without increasing system complexity. To validate the efficacy of our proposed method, we conducted comprehensive experiments using ads conversion model. Our experiments demonstrate that this method not only achieves high prediction accuracy but also does so more efficiently than other existing solutions. This validation underscores the potential of our Personalized Interpolation method to significantly enhance conversion optimization in real-world online advertising systems, promising improved targeting and effectiveness in advertising strategies.

Preference Discerning with LLM-Enhanced Generative Retrieval

Sequential recommendation systems aim to provide personalized recommendations for users based on their interaction history. To achieve this, they often incorporate auxiliary information, such as textual descriptions of items and auxiliary tasks, like predicting user preferences and intent. Despite numerous efforts to enhance these models, they still suffer from limited personalization. To address this issue, we propose a new paradigm, which we term preference discerning. In preference dscerning, we explicitly condition a generative sequential recommendation system on user preferences within its context. To this end, we generate user preferences using Large Language Models (LLMs) based on user reviews and item-specific data. To evaluate preference discerning capabilities of sequential recommendation systems, we introduce a novel benchmark that provides a holistic evaluation across various scenarios, including preference steering and sentiment following. We assess current state-of-the-art methods using our benchmark and show that they struggle to accurately discern user preferences. Therefore, we propose a new method named Mender ($\textbf{M}$ultimodal Prefer$\textbf{en}$ce $\textbf{d}$iscern$\textbf{er}$), which improves upon existing methods and achieves state-of-the-art performance on our benchmark. Our results show that Mender can be effectively guided by human preferences even though they have not been observed during training, paving the way toward more personalized sequential recommendation systems. We will open-source the code and benchmarks upon publication.

Unifying Generative and Dense Retrieval for Sequential Recommendation

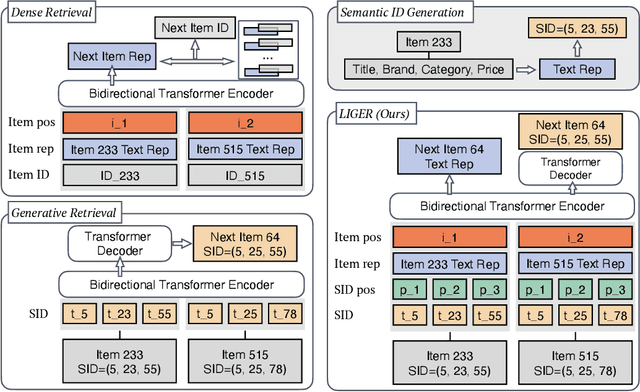
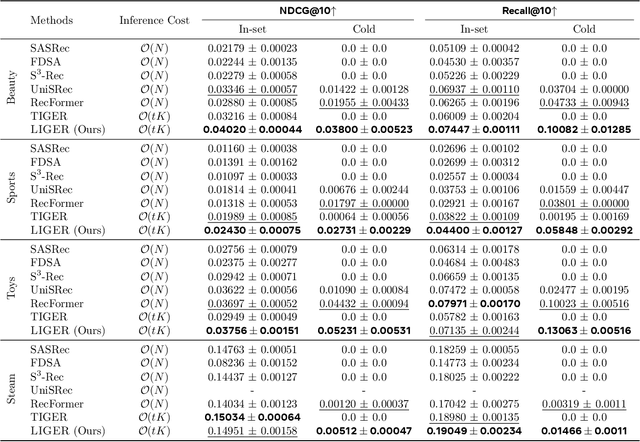
Sequential dense retrieval models utilize advanced sequence learning techniques to compute item and user representations, which are then used to rank relevant items for a user through inner product computation between the user and all item representations. However, this approach requires storing a unique representation for each item, resulting in significant memory requirements as the number of items grow. In contrast, the recently proposed generative retrieval paradigm offers a promising alternative by directly predicting item indices using a generative model trained on semantic IDs that encapsulate items' semantic information. Despite its potential for large-scale applications, a comprehensive comparison between generative retrieval and sequential dense retrieval under fair conditions is still lacking, leaving open questions regarding performance, and computation trade-offs. To address this, we compare these two approaches under controlled conditions on academic benchmarks and propose LIGER (LeveragIng dense retrieval for GEnerative Retrieval), a hybrid model that combines the strengths of these two widely used methods. LIGER integrates sequential dense retrieval into generative retrieval, mitigating performance differences and enhancing cold-start item recommendation in the datasets evaluated. This hybrid approach provides insights into the trade-offs between these approaches and demonstrates improvements in efficiency and effectiveness for recommendation systems in small-scale benchmarks.

TIES: Temporal Interaction Embeddings For Enhancing Social Media Integrity At Facebook

Since its inception, Facebook has become an integral part of the online social community. People rely on Facebook to make connections with others and build communities. As a result, it is paramount to protect the integrity of such a rapidly growing network in a fast and scalable manner. In this paper, we present our efforts to protect various social media entities at Facebook from people who try to abuse our platform. We present a novel Temporal Interaction EmbeddingS (TIES) model that is designed to capture rogue social interactions and flag them for further suitable actions. TIES is a supervised, deep learning, production ready model at Facebook-scale networks. Prior works on integrity problems are mostly focused on capturing either only static or certain dynamic features of social entities. In contrast, TIES can capture both these variant behaviors in a unified model owing to the recent strides made in the domains of graph embedding and deep sequential pattern learning. To show the real-world impact of TIES, we present a few applications especially for preventing spread of misinformation, fake account detection, and reducing ads payment risks in order to enhance the platform's integrity.

A Novel Stochastic Decoding of LDPC Codes with Quantitative Guarantees

Low-density parity-check codes, a class of capacity-approaching linear codes, are particularly recognized for their efficient decoding scheme. The decoding scheme, known as the sum-product, is an iterative algorithm consisting of passing messages between variable and check nodes of the factor graph. The sum-product algorithm is fully parallelizable, owing to the fact that all messages can be update concurrently. However, since it requires extensive number of highly interconnected wires, the fully-parallel implementation of the sum-product on chips is exceedingly challenging. Stochastic decoding algorithms, which exchange binary messages, are of great interest for mitigating this challenge and have been the focus of extensive research over the past decade. They significantly reduce the required wiring and computational complexity of the message-passing algorithm. Even though stochastic decoders have been shown extremely effective in practice, the theoretical aspect and understanding of such algorithms remains limited at large. Our main objective in this paper is to address this issue. We first propose a novel algorithm referred to as the Markov based stochastic decoding. Then, we provide concrete quantitative guarantees on its performance for tree-structured as well as general factor graphs. More specifically, we provide upper-bounds on the first and second moments of the error, illustrating that the proposed algorithm is an asymptotically consistent estimate of the sum-product algorithm. We also validate our theoretical predictions with experimental results, showing we achieve comparable performance to other practical stochastic decoders.

Belief Propagation for Continuous State Spaces: Stochastic Message-Passing with Quantitative Guarantees

The sum-product or belief propagation (BP) algorithm is a widely used message-passing technique for computing approximate marginals in graphical models. We introduce a new technique, called stochastic orthogonal series message-passing (SOSMP), for computing the BP fixed point in models with continuous random variables. It is based on a deterministic approximation of the messages via orthogonal series expansion, and a stochastic approximation via Monte Carlo estimates of the integral updates of the basis coefficients. We prove that the SOSMP iterates converge to a \delta-neighborhood of the unique BP fixed point for any tree-structured graph, and for any graphs with cycles in which the BP updates satisfy a contractivity condition. In addition, we demonstrate how to choose the number of basis coefficients as a function of the desired approximation accuracy \delta and smoothness of the compatibility functions. We illustrate our theory with both simulated examples and in application to optical flow estimation.

Stochastic Belief Propagation: A Low-Complexity Alternative to the Sum-Product Algorithm

The sum-product or belief propagation (BP) algorithm is a widely-used message-passing algorithm for computing marginal distributions in graphical models with discrete variables. At the core of the BP message updates, when applied to a graphical model with pairwise interactions, lies a matrix-vector product with complexity that is quadratic in the state dimension $d$, and requires transmission of a $(d-1)$-dimensional vector of real numbers (messages) to its neighbors. Since various applications involve very large state dimensions, such computation and communication complexities can be prohibitively complex. In this paper, we propose a low-complexity variant of BP, referred to as stochastic belief propagation (SBP). As suggested by the name, it is an adaptively randomized version of the BP message updates in which each node passes randomly chosen information to each of its neighbors. The SBP message updates reduce the computational complexity (per iteration) from quadratic to linear in $d$, without assuming any particular structure of the potentials, and also reduce the communication complexity significantly, requiring only $\log{d}$ bits transmission per edge. Moreover, we establish a number of theoretical guarantees for the performance of SBP, showing that it converges almost surely to the BP fixed point for any tree-structured graph, and for graphs with cycles satisfying a contractivity condition. In addition, for these graphical models, we provide non-asymptotic upper bounds on the convergence rate, showing that the $\ell_{\infty}$ norm of the error vector decays no slower than $O(1/\sqrt{t})$ with the number of iterations $t$ on trees and the mean square error decays as $O(1/t)$ for general graphs. These analysis show that SBP can provably yield reductions in computational and communication complexities for various classes of graphical models.