RAD: Region-Aware Diffusion Models for Image Inpainting

Diffusion models have achieved remarkable success in image generation, with applications broadening across various domains. Inpainting is one such application that can benefit significantly from diffusion models. Existing methods either hijack the reverse process of a pretrained diffusion model or cast the problem into a larger framework, \ie, conditioned generation. However, these approaches often require nested loops in the generation process or additional components for conditioning. In this paper, we present region-aware diffusion models (RAD) for inpainting with a simple yet effective reformulation of the vanilla diffusion models. RAD utilizes a different noise schedule for each pixel, which allows local regions to be generated asynchronously while considering the global image context. A plain reverse process requires no additional components, enabling RAD to achieve inference time up to 100 times faster than the state-of-the-art approaches. Moreover, we employ low-rank adaptation (LoRA) to fine-tune RAD based on other pretrained diffusion models, reducing computational burdens in training as well. Experiments demonstrated that RAD provides state-of-the-art results both qualitatively and quantitatively, on the FFHQ, LSUN Bedroom, and ImageNet datasets.

EnSiam: Self-Supervised Learning With Ensemble Representations

Recently, contrastive self-supervised learning, where the proximity of representations is determined based on the identities of samples, has made remarkable progress in unsupervised representation learning. SimSiam is a well-known example in this area, known for its simplicity yet powerful performance. However, it is known to be sensitive to changes in training configurations, such as hyperparameters and augmentation settings, due to its structural characteristics. To address this issue, we focus on the similarity between contrastive learning and the teacher-student framework in knowledge distillation. Inspired by the ensemble-based knowledge distillation approach, the proposed method, EnSiam, aims to improve the contrastive learning procedure using ensemble representations. This can provide stable pseudo labels, providing better performance. Experiments demonstrate that EnSiam outperforms previous state-of-the-art methods in most cases, including the experiments on ImageNet, which shows that EnSiam is capable of learning high-quality representations.

Procrustean Regression Networks: Learning 3D Structure of Non-Rigid Objects from 2D Annotations

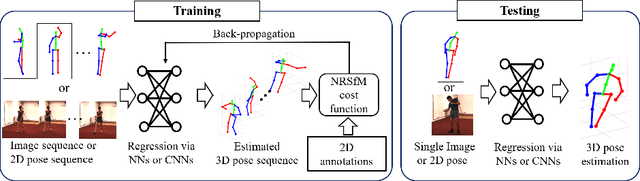
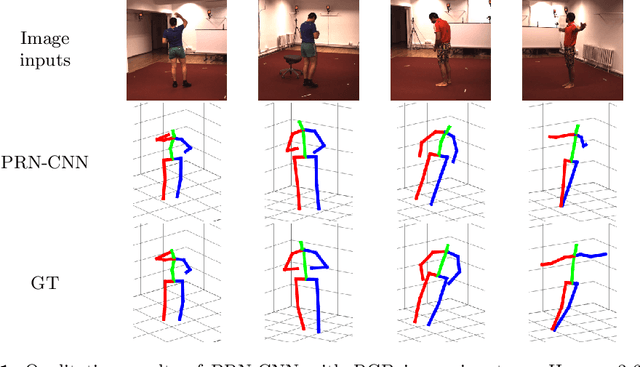
We propose a novel framework for training neural networks which is capable of learning 3D information of non-rigid objects when only 2D annotations are available as ground truths. Recently, there have been some approaches that incorporate the problem setting of non-rigid structure-from-motion (NRSfM) into deep learning to learn 3D structure reconstruction. The most important difficulty of NRSfM is to estimate both the rotation and deformation at the same time, and previous works handle this by regressing both of them. In this paper, we resolve this difficulty by proposing a loss function wherein the suitable rotation is automatically determined. Trained with the cost function consisting of the reprojection error and the low-rank term of aligned shapes, the network learns the 3D structures of such objects as human skeletons and faces during the training, whereas the testing is done in a single-frame basis. The proposed method can handle inputs with missing entries and experimental results validate that the proposed framework shows superior reconstruction performance to the state-of-the-art method on the Human 3.6M, 300-VW, and SURREAL datasets, even though the underlying network structure is very simple.

Differentiable Fixed-Point Iteration Layer

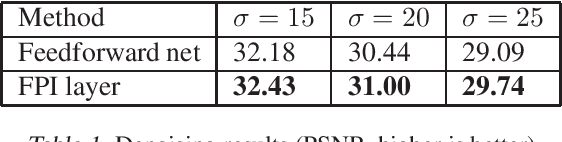
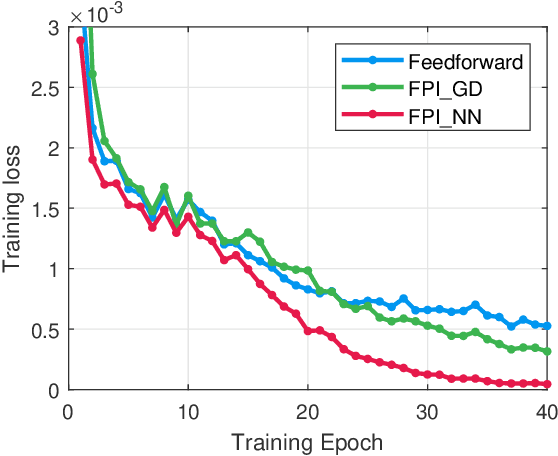
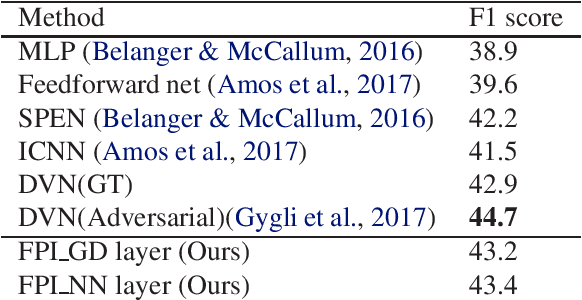
Recently, several studies proposed methods to utilize some restricted classes of optimization problems as layers of deep neural networks. However, these methods are still in their infancy and require special treatments, i.e., analyzing the KKT condition, etc., for deriving the backpropagation formula. Instead, in this paper, we propose a method to utilize fixed-point iteration (FPI), a generalization of many types of numerical algorithms, as a network layer. We show that the derivative of an FPI layer depends only on the fixed point, and then we present a method to calculate it efficiently using another FPI which we call the backward FPI. The proposed method can be easily implemented based on the autograd functionalities in existing deep learning tools. Since FPI covers vast different types of numerical algorithms in machine learning and other fields, it has a lot of potential applications. In the experiments, the differentiable FPI layer is applied to two scenarios, i.e., gradient descent iterations for differentiable optimization problems and FPI with arbitrary neural network modules, of which the results demonstrate the simplicity and the effectiveness.

Symmetric Graph Convolutional Autoencoder for Unsupervised Graph Representation Learning

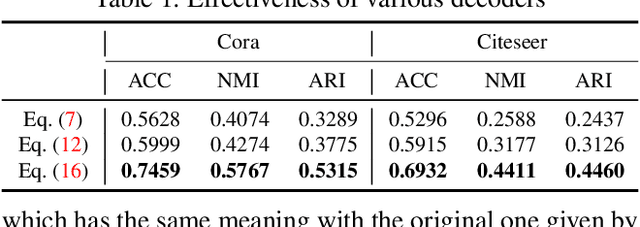
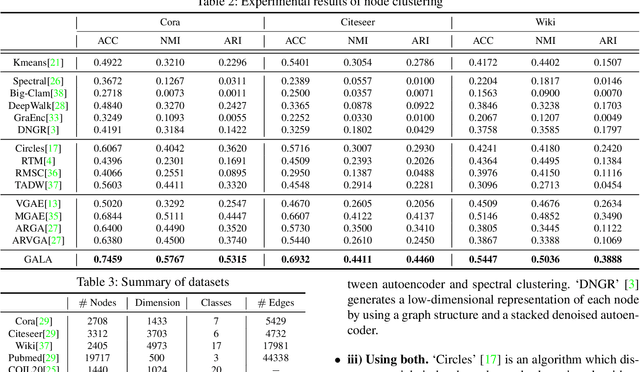
We propose a symmetric graph convolutional autoencoder which produces a low-dimensional latent representation from a graph. In contrast to the existing graph autoencoders with asymmetric decoder parts, the proposed autoencoder has a newly designed decoder which builds a completely symmetric autoencoder form. For the reconstruction of node features, the decoder is designed based on Laplacian sharpening as the counterpart of Laplacian smoothing of the encoder, which allows utilizing the graph structure in the whole processes of the proposed autoencoder architecture. In order to prevent the numerical instability of the network caused by the Laplacian sharpening introduction, we further propose a new numerically stable form of the Laplacian sharpening by incorporating the signed graphs. In addition, a new cost function which finds a latent representation and a latent affinity matrix simultaneously is devised to boost the performance of image clustering tasks. The experimental results on clustering, link prediction and visualization tasks strongly support that the proposed model is stable and outperforms various state-of-the-art algorithms.

Neuro-Optimization: Learning Objective Functions Using Neural Networks

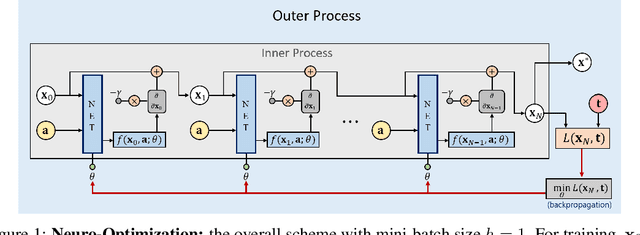
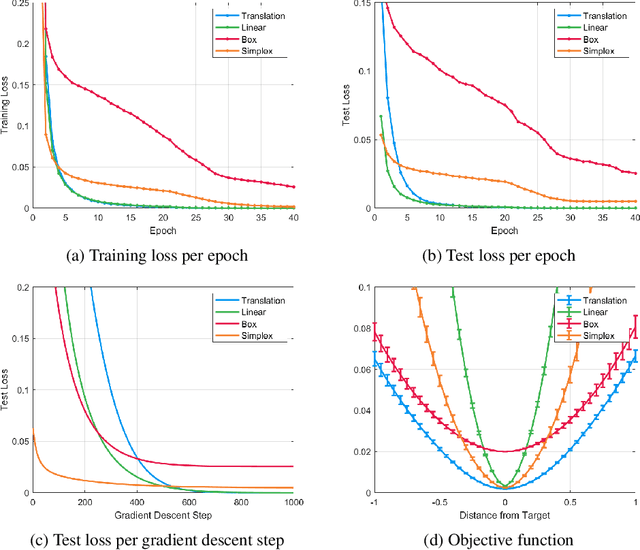
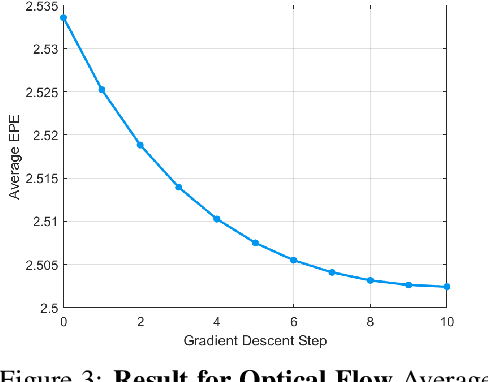
Mathematical optimization is widely used in various research fields. With a carefully-designed objective function, mathematical optimization can be quite helpful in solving many problems. However, objective functions are usually hand-crafted and designing a good one can be quite challenging. In this paper, we propose a novel framework to learn the objective function based on a neural net-work. The basic idea is to consider the neural network as an objective function, and the input as an optimization variable. For the learning of objective function from the training data, two processes are conducted: In the inner process, the optimization variable (the input of the network) are optimized to minimize the objective function (the network output), while fixing the network weights. In the outer process, on the other hand, the weights are optimized based on how close the final solution of the inner process is to the desired solution. After learning the objective function, the solution for the test set is obtained in the same manner of the inner process. The potential and applicability of our approach are demonstrated by the experiments on toy examples and a computer vision task, optical flow.

Knowledge Transfer via Distillation of Activation Boundaries Formed by Hidden Neurons

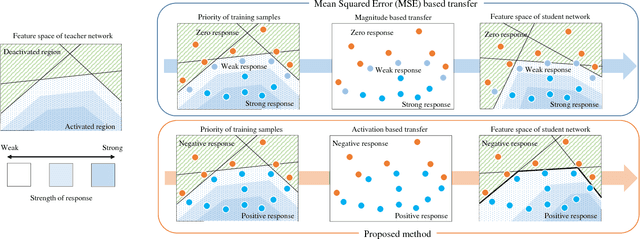
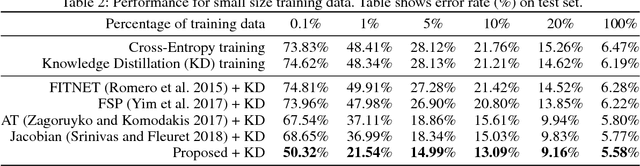
An activation boundary for a neuron refers to a separating hyperplane that determines whether the neuron is activated or deactivated. It has been long considered in neural networks that the activations of neurons, rather than their exact output values, play the most important role in forming classification friendly partitions of the hidden feature space. However, as far as we know, this aspect of neural networks has not been considered in the literature of knowledge transfer. In this paper, we propose a knowledge transfer method via distillation of activation boundaries formed by hidden neurons. For the distillation, we propose an activation transfer loss that has the minimum value when the boundaries generated by the student coincide with those by the teacher. Since the activation transfer loss is not differentiable, we design a piecewise differentiable loss approximating the activation transfer loss. By the proposed method, the student learns a separating boundary between activation region and deactivation region formed by each neuron in the teacher. Through the experiments in various aspects of knowledge transfer, it is verified that the proposed method outperforms the current state-of-the-art.

Knowledge Distillation with Adversarial Samples Supporting Decision Boundary

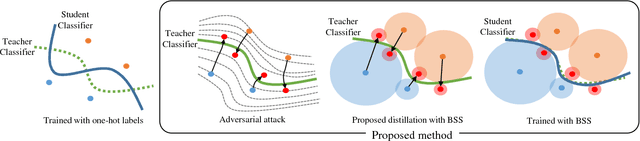
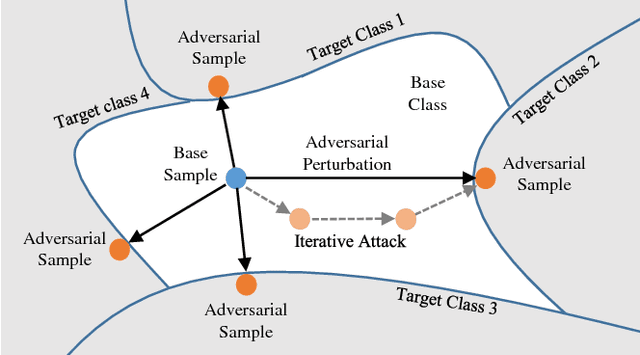
Many recent works on knowledge distillation have provided ways to transfer the knowledge of a trained network for improving the learning process of a new one, but finding a good technique for knowledge distillation is still an open problem. In this paper, we provide a new perspective based on a decision boundary, which is one of the most important component of a classifier. The generalization performance of a classifier is closely related to the adequacy of its decision boundary, so a good classifier bears a good decision boundary. Therefore, transferring information closely related to the decision boundary can be a good attempt for knowledge distillation. To realize this goal, we utilize an adversarial attack to discover samples supporting a decision boundary. Based on this idea, to transfer more accurate information about the decision boundary, the proposed algorithm trains a student classifier based on the adversarial samples supporting the decision boundary. Experiments show that the proposed method indeed improves knowledge distillation and achieves the state-of-the-arts performance.

Deep Pose Consensus Networks

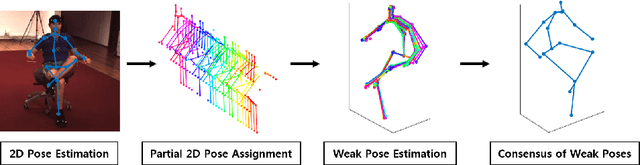
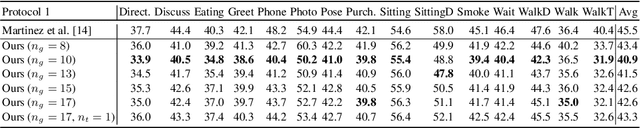
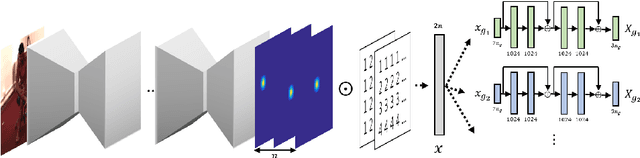
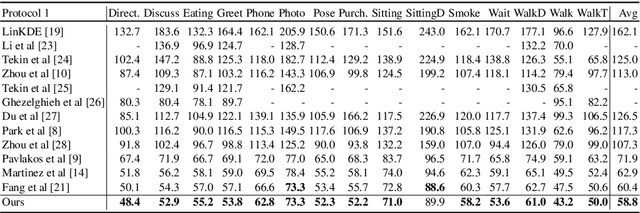
In this paper, we address the problem of estimating a 3D human pose from a single image, which is important but difficult to solve due to many reasons, such as self-occlusions, wild appearance changes, and inherent ambiguities of 3D estimation from a 2D cue. These difficulties make the problem ill-posed, which have become requiring increasingly complex estimators to enhance the performance. On the other hand, most existing methods try to handle this problem based on a single complex estimator, which might not be good solutions. In this paper, to resolve this issue, we propose a multiple-partial-hypothesis-based framework for the problem of estimating 3D human pose from a single image, which can be fine-tuned in an end-to-end fashion. We first select several joint groups from a human joint model using the proposed sampling scheme, and estimate the 3D poses of each joint group separately based on deep neural networks. After that, they are aggregated to obtain the final 3D poses using the proposed robust optimization formula. The overall procedure can be fine-tuned in an end-to-end fashion, resulting in better performance. In the experiments, the proposed framework shows the state-of-the-art performances on popular benchmark data sets, namely Human3.6M and HumanEva, which demonstrate the effectiveness of the proposed framework.