Symmetric Graph Convolutional Autoencoder for Unsupervised Graph Representation Learning
Paper and Code
Aug 07, 2019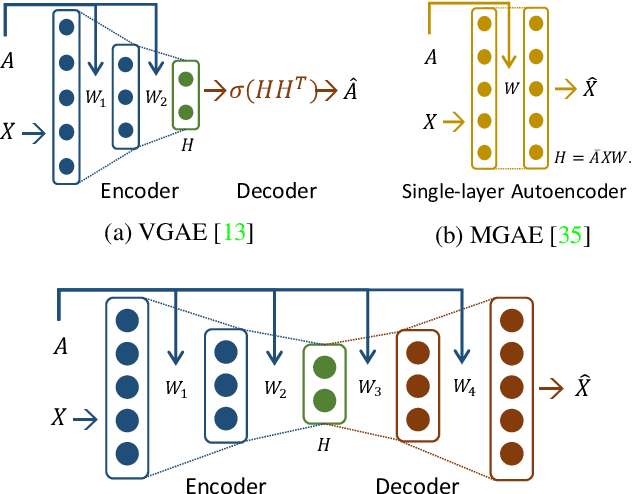
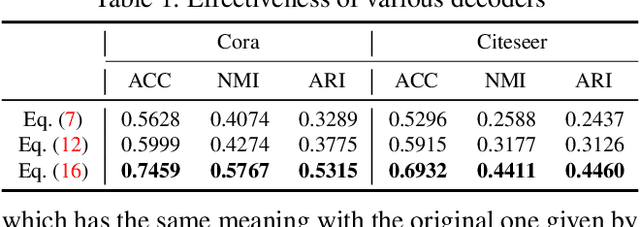

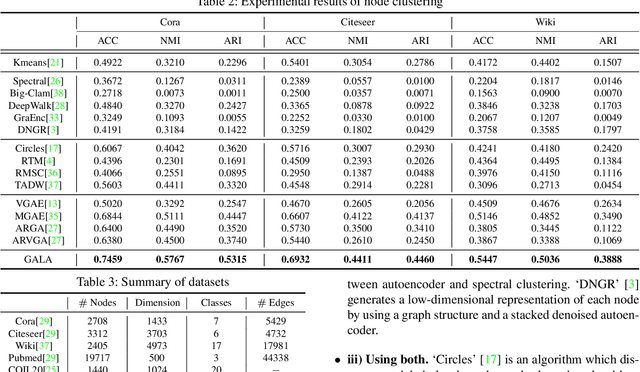
We propose a symmetric graph convolutional autoencoder which produces a low-dimensional latent representation from a graph. In contrast to the existing graph autoencoders with asymmetric decoder parts, the proposed autoencoder has a newly designed decoder which builds a completely symmetric autoencoder form. For the reconstruction of node features, the decoder is designed based on Laplacian sharpening as the counterpart of Laplacian smoothing of the encoder, which allows utilizing the graph structure in the whole processes of the proposed autoencoder architecture. In order to prevent the numerical instability of the network caused by the Laplacian sharpening introduction, we further propose a new numerically stable form of the Laplacian sharpening by incorporating the signed graphs. In addition, a new cost function which finds a latent representation and a latent affinity matrix simultaneously is devised to boost the performance of image clustering tasks. The experimental results on clustering, link prediction and visualization tasks strongly support that the proposed model is stable and outperforms various state-of-the-art algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge