Younahan Jeon
Differentiable Fixed-Point Iteration Layer
Feb 07, 2020
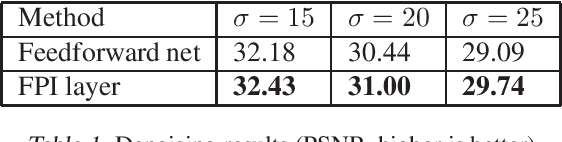
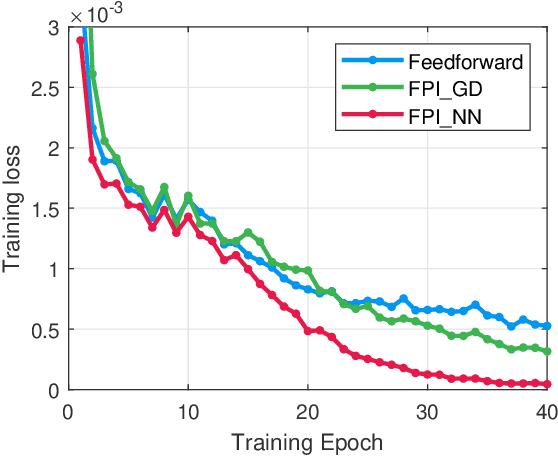
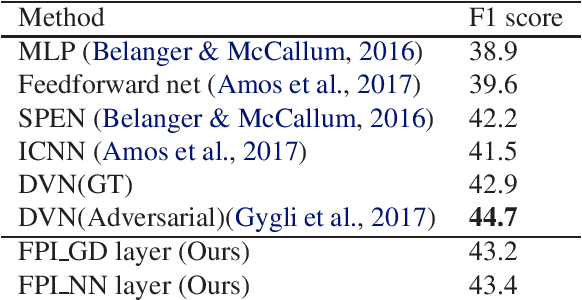
Abstract:Recently, several studies proposed methods to utilize some restricted classes of optimization problems as layers of deep neural networks. However, these methods are still in their infancy and require special treatments, i.e., analyzing the KKT condition, etc., for deriving the backpropagation formula. Instead, in this paper, we propose a method to utilize fixed-point iteration (FPI), a generalization of many types of numerical algorithms, as a network layer. We show that the derivative of an FPI layer depends only on the fixed point, and then we present a method to calculate it efficiently using another FPI which we call the backward FPI. The proposed method can be easily implemented based on the autograd functionalities in existing deep learning tools. Since FPI covers vast different types of numerical algorithms in machine learning and other fields, it has a lot of potential applications. In the experiments, the differentiable FPI layer is applied to two scenarios, i.e., gradient descent iterations for differentiable optimization problems and FPI with arbitrary neural network modules, of which the results demonstrate the simplicity and the effectiveness.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge