Younghan Jeon
Influence-Balanced Loss for Imbalanced Visual Classification
Oct 06, 2021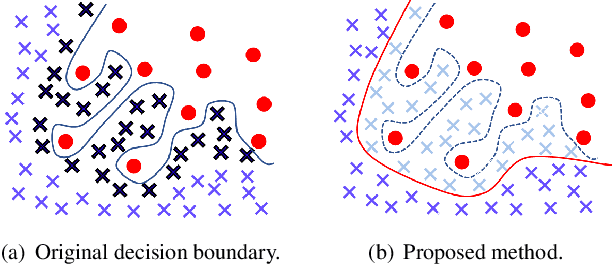
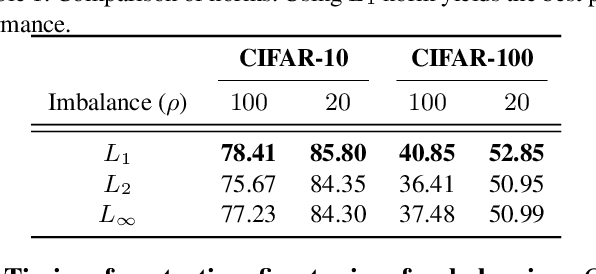
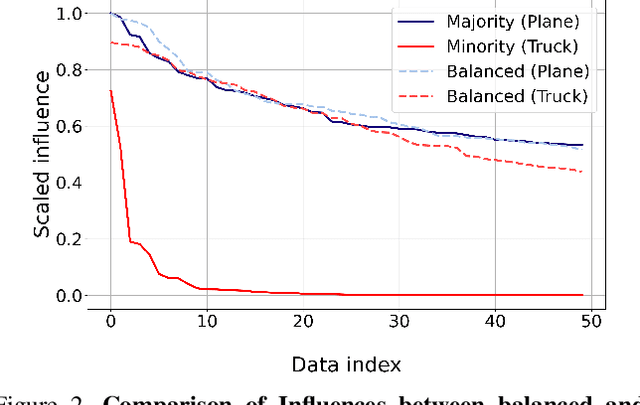
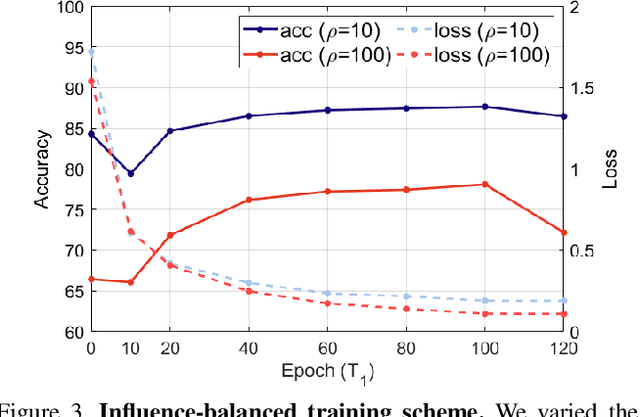
Abstract:In this paper, we propose a balancing training method to address problems in imbalanced data learning. To this end, we derive a new loss used in the balancing training phase that alleviates the influence of samples that cause an overfitted decision boundary. The proposed loss efficiently improves the performance of any type of imbalance learning methods. In experiments on multiple benchmark data sets, we demonstrate the validity of our method and reveal that the proposed loss outperforms the state-of-the-art cost-sensitive loss methods. Furthermore, since our loss is not restricted to a specific task, model, or training method, it can be easily used in combination with other recent re-sampling, meta-learning, and cost-sensitive learning methods for class-imbalance problems.
* Published in ICCV 2021
Neuro-Optimization: Learning Objective Functions Using Neural Networks
May 24, 2019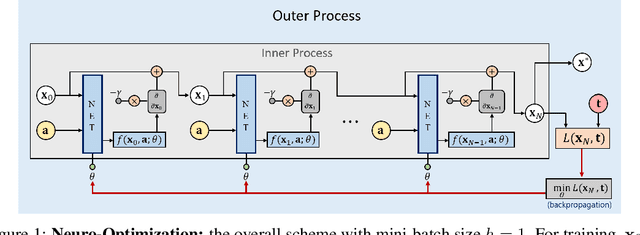
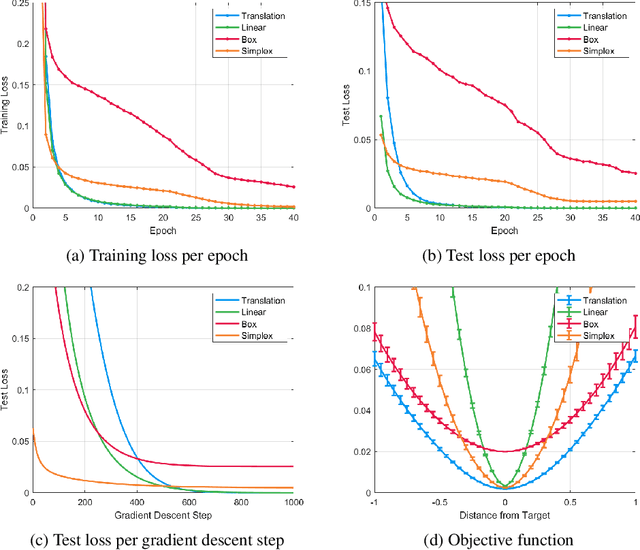
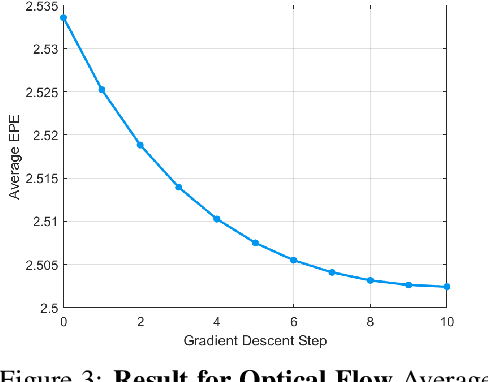
Abstract:Mathematical optimization is widely used in various research fields. With a carefully-designed objective function, mathematical optimization can be quite helpful in solving many problems. However, objective functions are usually hand-crafted and designing a good one can be quite challenging. In this paper, we propose a novel framework to learn the objective function based on a neural net-work. The basic idea is to consider the neural network as an objective function, and the input as an optimization variable. For the learning of objective function from the training data, two processes are conducted: In the inner process, the optimization variable (the input of the network) are optimized to minimize the objective function (the network output), while fixing the network weights. In the outer process, on the other hand, the weights are optimized based on how close the final solution of the inner process is to the desired solution. After learning the objective function, the solution for the test set is obtained in the same manner of the inner process. The potential and applicability of our approach are demonstrated by the experiments on toy examples and a computer vision task, optical flow.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge