From Orbit to Ground: Generative City Photogrammetry from Extreme Off-Nadir Satellite Images

City-scale 3D reconstruction from satellite imagery presents the challenge of extreme viewpoint extrapolation, where our goal is to synthesize ground-level novel views from sparse orbital images with minimal parallax. This requires inferring nearly $90^\circ$ viewpoint gaps from image sources with severely foreshortened facades and flawed textures, causing state-of-the-art reconstruction engines such as NeRF and 3DGS to fail. To address this problem, we propose two design choices tailored for city structures and satellite inputs. First, we model city geometry as a 2.5D height map, implemented as a Z-monotonic signed distance field (SDF) that matches urban building layouts from top-down viewpoints. This stabilizes geometry optimization under sparse, off-nadir satellite views and yields a watertight mesh with crisp roofs and clean, vertically extruded facades. Second, we paint the mesh appearance from satellite images via differentiable rendering techniques. While the satellite inputs may contain long-range, blurry captures, we further train a generative texture restoration network to enhance the appearance, recovering high-frequency, plausible texture details from degraded inputs. Our method's scalability and robustness are demonstrated through extensive experiments on large-scale urban reconstruction. For example, in our teaser figure, we reconstruct a $4\,\mathrm{km}^2$ real-world region from only a few satellite images, achieving state-of-the-art performance in synthesizing photorealistic ground views. The resulting models are not only visually compelling but also serve as high-fidelity, application-ready assets for downstream tasks like urban planning and simulation. Project page can be found at https://pku-vcl-geometry.github.io/Orbit2Ground/.

DO-Conv: Depthwise Over-parameterized Convolutional Layer

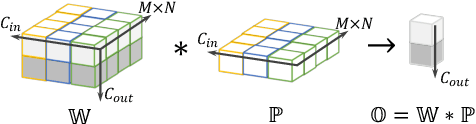
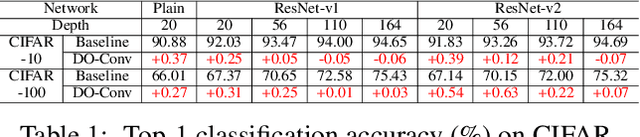
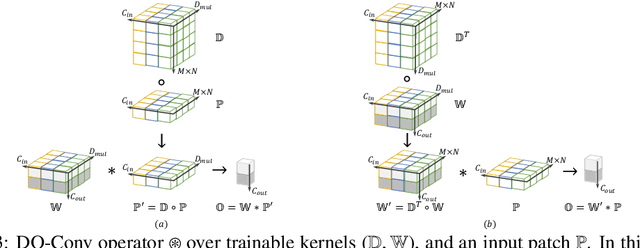
Convolutional layers are the core building blocks of Convolutional Neural Networks (CNNs). In this paper, we propose to augment a convolutional layer with an additional depthwise convolution, where each input channel is convolved with a different 2D kernel. The composition of the two convolutions constitutes an over-parameterization, since it adds learnable parameters, while the resulting linear operation can be expressed by a single convolution layer. We refer to this depthwise over-parameterized convolutional layer as DO-Conv. We show with extensive experiments that the mere replacement of conventional convolutional layers with DO-Conv layers boosts the performance of CNNs on many classical vision tasks, such as image classification, detection, and segmentation. Moreover, in the inference phase, the depthwise convolution is folded into the conventional convolution, reducing the computation to be exactly equivalent to that of a convolutional layer without over-parameterization. As DO-Conv introduces performance gains without incurring any computational complexity increase for inference, we advocate it as an alternative to the conventional convolutional layer. We open-source a reference implementation of DO-Conv in Tensorflow, PyTorch and GluonCV at https://github.com/yangyanli/DO-Conv.

Neighborhood Enlargement in Graph Neural Networks

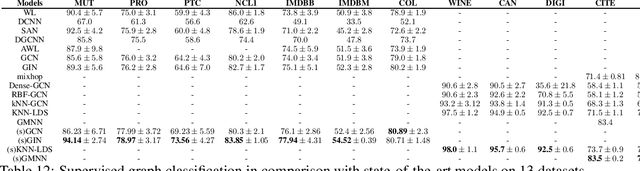
Graph Neural Network (GNN) is an effective framework for representation learning and prediction for graph structural data. A neighborhood aggregation scheme is applied in the training of GNN and variants, that representation of each node is calculated through recursively aggregating and transforming representation of the neighboring nodes. A variety of GNNS and the variants are build and have achieved state-of-the-art results on both node and graph classification tasks. However, despite common neighborhood which is used in the state-of-the-art GNN models, there is little analysis on the properties of the neighborhood in the neighborhood aggregation scheme. Here, we analyze the properties of the node, edges, and neighborhood of the graph model. Our results characterize the efficiency of the common neighborhood used in the state-of-the-art GNNs, and show that it is not sufficient for the representation learning of the nodes. We propose a simple neighborhood which is likely to be more sufficient. We empirically validate our theoretical analysis on a number of graph classification benchmarks and demonstrate that our methods achieve state-of-the-art performance on listed benchmarks. The implementation code is available at \url{https://github.com/CODE-SUBMIT/Neighborhood-Enlargement-in-Graph-Network}.

PointCNN: Convolution On $\mathcal{X}$-Transformed Points

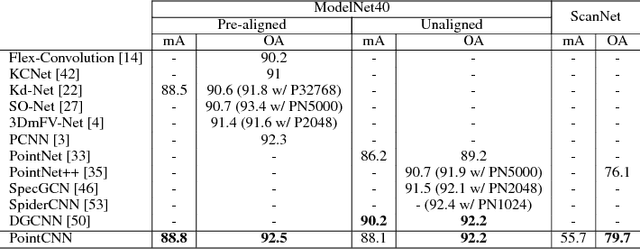
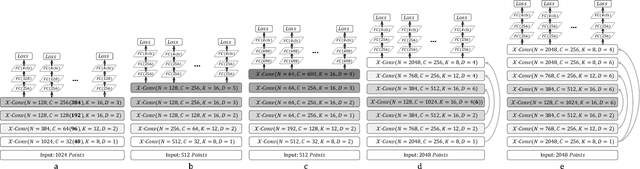
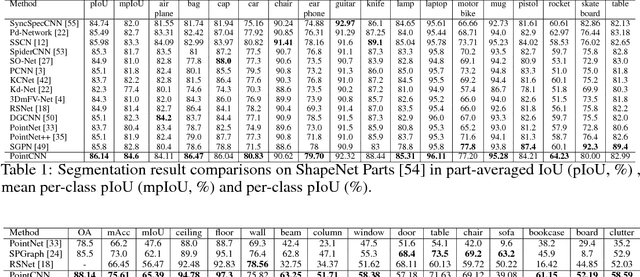
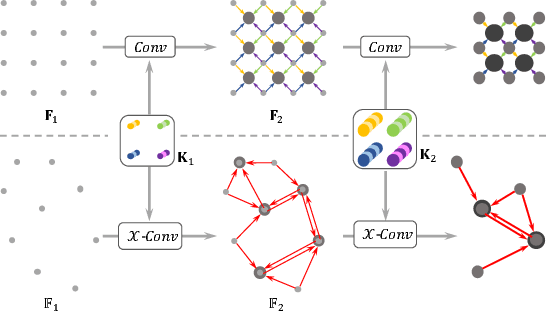
We present a simple and general framework for feature learning from point clouds. The key to the success of CNNs is the convolution operator that is capable of leveraging spatially-local correlation in data represented densely in grids (e.g. images). However, point clouds are irregular and unordered, thus directly convolving kernels against features associated with the points, will result in desertion of shape information and variance to point ordering. To address these problems, we propose to learn an $\mathcal{X}$-transformation from the input points, to simultaneously promote two causes. The first is the weighting of the input features associated with the points, and the second is the permutation of the points into a latent and potentially canonical order. Element-wise product and sum operations of the typical convolution operator are subsequently applied on the $\mathcal{X}$-transformed features. The proposed method is a generalization of typical CNNs to feature learning from point clouds, thus we call it PointCNN. Experiments show that PointCNN achieves on par or better performance than state-of-the-art methods on multiple challenging benchmark datasets and tasks.

Large-Scale 3D Shape Reconstruction and Segmentation from ShapeNet Core55

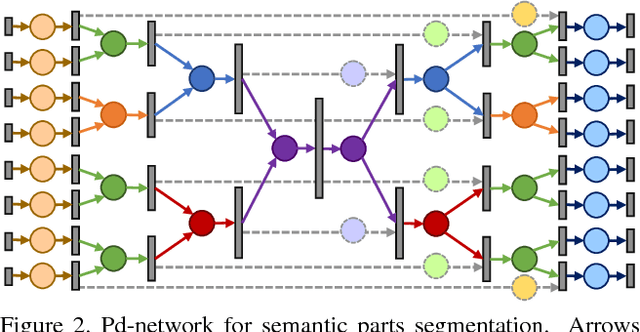
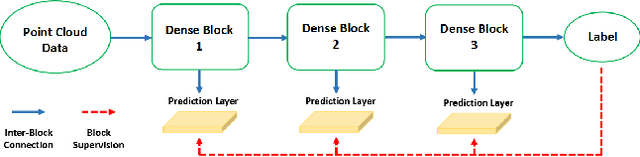
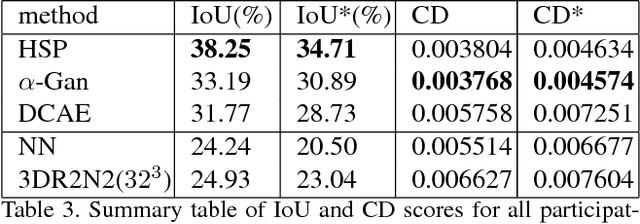
We introduce a large-scale 3D shape understanding benchmark using data and annotation from ShapeNet 3D object database. The benchmark consists of two tasks: part-level segmentation of 3D shapes and 3D reconstruction from single view images. Ten teams have participated in the challenge and the best performing teams have outperformed state-of-the-art approaches on both tasks. A few novel deep learning architectures have been proposed on various 3D representations on both tasks. We report the techniques used by each team and the corresponding performances. In addition, we summarize the major discoveries from the reported results and possible trends for the future work in the field.