Rui Bu
Neighborhood Enlargement in Graph Neural Networks
May 21, 2019


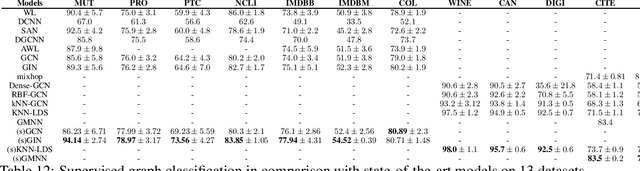
Abstract:Graph Neural Network (GNN) is an effective framework for representation learning and prediction for graph structural data. A neighborhood aggregation scheme is applied in the training of GNN and variants, that representation of each node is calculated through recursively aggregating and transforming representation of the neighboring nodes. A variety of GNNS and the variants are build and have achieved state-of-the-art results on both node and graph classification tasks. However, despite common neighborhood which is used in the state-of-the-art GNN models, there is little analysis on the properties of the neighborhood in the neighborhood aggregation scheme. Here, we analyze the properties of the node, edges, and neighborhood of the graph model. Our results characterize the efficiency of the common neighborhood used in the state-of-the-art GNNs, and show that it is not sufficient for the representation learning of the nodes. We propose a simple neighborhood which is likely to be more sufficient. We empirically validate our theoretical analysis on a number of graph classification benchmarks and demonstrate that our methods achieve state-of-the-art performance on listed benchmarks. The implementation code is available at \url{https://github.com/CODE-SUBMIT/Neighborhood-Enlargement-in-Graph-Network}.
PointCNN: Convolution On $\mathcal{X}$-Transformed Points
Nov 05, 2018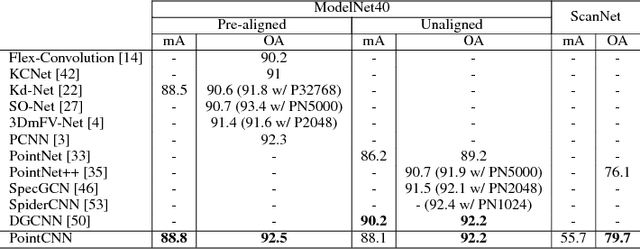
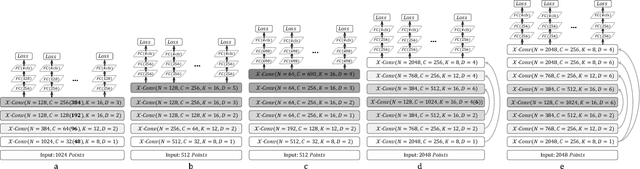
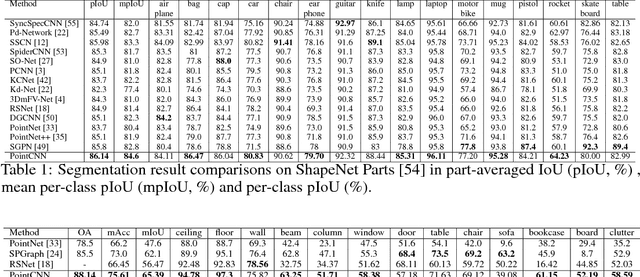
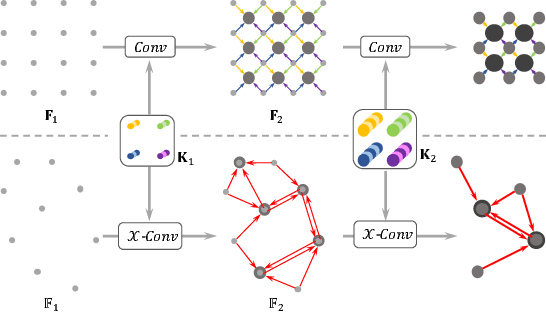
Abstract:We present a simple and general framework for feature learning from point clouds. The key to the success of CNNs is the convolution operator that is capable of leveraging spatially-local correlation in data represented densely in grids (e.g. images). However, point clouds are irregular and unordered, thus directly convolving kernels against features associated with the points, will result in desertion of shape information and variance to point ordering. To address these problems, we propose to learn an $\mathcal{X}$-transformation from the input points, to simultaneously promote two causes. The first is the weighting of the input features associated with the points, and the second is the permutation of the points into a latent and potentially canonical order. Element-wise product and sum operations of the typical convolution operator are subsequently applied on the $\mathcal{X}$-transformed features. The proposed method is a generalization of typical CNNs to feature learning from point clouds, thus we call it PointCNN. Experiments show that PointCNN achieves on par or better performance than state-of-the-art methods on multiple challenging benchmark datasets and tasks.
Large-Scale 3D Shape Reconstruction and Segmentation from ShapeNet Core55
Oct 27, 2017
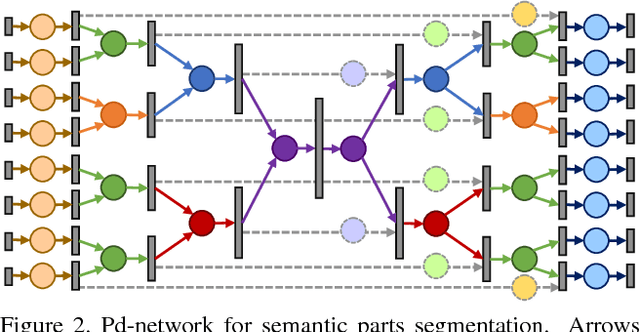
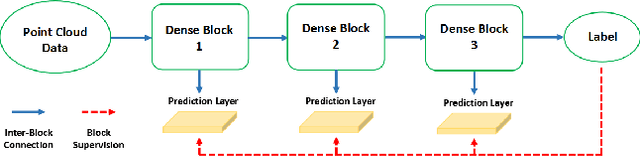
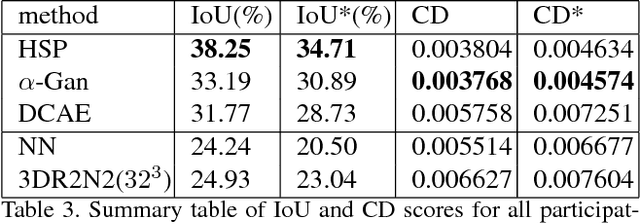
Abstract:We introduce a large-scale 3D shape understanding benchmark using data and annotation from ShapeNet 3D object database. The benchmark consists of two tasks: part-level segmentation of 3D shapes and 3D reconstruction from single view images. Ten teams have participated in the challenge and the best performing teams have outperformed state-of-the-art approaches on both tasks. A few novel deep learning architectures have been proposed on various 3D representations on both tasks. We report the techniques used by each team and the corresponding performances. In addition, we summarize the major discoveries from the reported results and possible trends for the future work in the field.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge