Vision-Language Models as a Source of Rewards

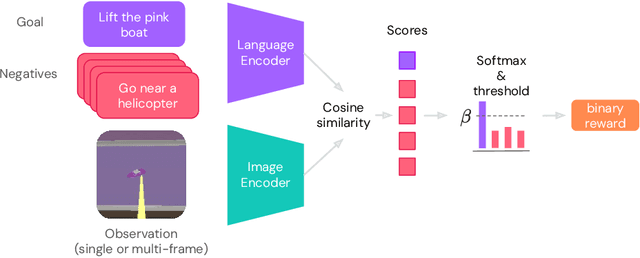
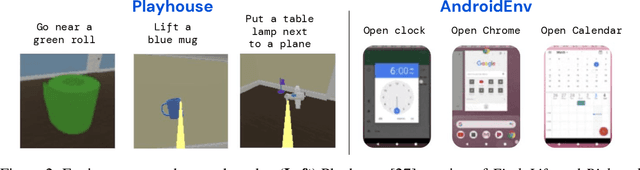
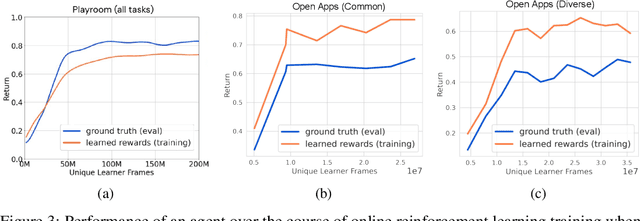
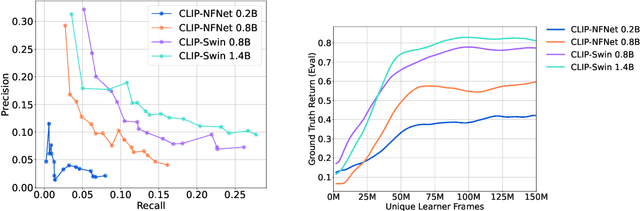
Building generalist agents that can accomplish many goals in rich open-ended environments is one of the research frontiers for reinforcement learning. A key limiting factor for building generalist agents with RL has been the need for a large number of reward functions for achieving different goals. We investigate the feasibility of using off-the-shelf vision-language models, or VLMs, as sources of rewards for reinforcement learning agents. We show how rewards for visual achievement of a variety of language goals can be derived from the CLIP family of models, and used to train RL agents that can achieve a variety of language goals. We showcase this approach in two distinct visual domains and present a scaling trend showing how larger VLMs lead to more accurate rewards for visual goal achievement, which in turn produces more capable RL agents.

In-context Reinforcement Learning with Algorithm Distillation

We propose Algorithm Distillation (AD), a method for distilling reinforcement learning (RL) algorithms into neural networks by modeling their training histories with a causal sequence model. Algorithm Distillation treats learning to reinforcement learn as an across-episode sequential prediction problem. A dataset of learning histories is generated by a source RL algorithm, and then a causal transformer is trained by autoregressively predicting actions given their preceding learning histories as context. Unlike sequential policy prediction architectures that distill post-learning or expert sequences, AD is able to improve its policy entirely in-context without updating its network parameters. We demonstrate that AD can reinforcement learn in-context in a variety of environments with sparse rewards, combinatorial task structure, and pixel-based observations, and find that AD learns a more data-efficient RL algorithm than the one that generated the source data.

Higher Order Generalization Error for First Order Discretization of Langevin Diffusion

We propose a novel approach to analyze generalization error for discretizations of Langevin diffusion, such as the stochastic gradient Langevin dynamics (SGLD). For an $\epsilon$ tolerance of expected generalization error, it is known that a first order discretization can reach this target if we run $\Omega(\epsilon^{-1} \log (\epsilon^{-1}) )$ iterations with $\Omega(\epsilon^{-1})$ samples. In this article, we show that with additional smoothness assumptions, even first order methods can achieve arbitrarily runtime complexity. More precisely, for each $N>0$, we provide a sufficient smoothness condition on the loss function such that a first order discretization can reach $\epsilon$ expected generalization error given $\Omega( \epsilon^{-1/N} \log (\epsilon^{-1}) )$ iterations with $\Omega(\epsilon^{-1})$ samples.

Interplay Between Optimization and Generalization of Stochastic Gradient Descent with Covariance Noise

The choice of batch-size in a stochastic optimization algorithm plays a substantial role for both optimization and generalization. Increasing the batch-size used typically improves optimization but degrades generalization. To address the problem of improving generalization while maintaining optimal convergence in large-batch training, we propose to add covariance noise to the gradients. We demonstrate that the optimization performance of our method is more accurately captured by the structure of the noise covariance matrix rather than by the variance of gradients. Moreover, over the convex-quadratic, we prove in theory that it can be characterized by the Frobenius norm of the noise matrix. Our empirical studies with standard deep learning model-architectures and datasets shows that our method not only improves generalization performance in large-batch training, but furthermore, does so in a way where the optimization performance remains desirable and the training duration is not elongated.

A general system of differential equations to model first order adaptive algorithms

First order optimization algorithms play a major role in large scale machine learning. A new class of methods, called adaptive algorithms, were recently introduced to adjust iteratively the learning rate for each coordinate. Despite great practical success in deep learning, their behavior and performance on more general loss functions are not well understood. In this paper, we derive a non-autonomous system of differential equations, which is the continuous time limit of adaptive optimization methods. We prove global well-posedness of the system and we investigate the numerical time convergence of its forward Euler approximation. We study, furthermore, the convergence of its trajectories and give conditions under which the differential system, underlying all adaptive algorithms, is suitable for optimization. We discuss convergence to a critical point in the non-convex case and give conditions for the dynamics to avoid saddle points and local maxima. For convex and deterministic loss function, we introduce a suitable Lyapunov functional which allow us to study its rate of convergence. Several other properties of both the continuous and discrete systems are briefly discussed. The differential system studied in the paper is general enough to encompass many other classical algorithms (such as Heavy ball and Nesterov's accelerated method) and allow us to recover several known results for these algorithms.

Scalable Recommender Systems through Recursive Evidence Chains

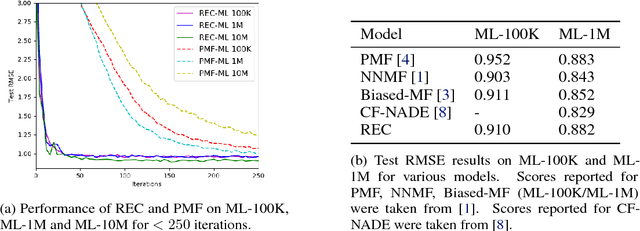
Recommender systems can be formulated as a matrix completion problem, predicting ratings from user and item parameter vectors. Optimizing these parameters by subsampling data becomes difficult as the number of users and items grows. We develop a novel approach to generate all latent variables on demand from the ratings matrix itself and a fixed pool of parameters. We estimate missing ratings using chains of evidence that link them to a small set of prototypical users and items. Our model automatically addresses the cold-start and online learning problems by combining information across both users and items. We investigate the scaling behavior of this model, and demonstrate competitive results with respect to current matrix factorization techniques in terms of accuracy and convergence speed.

Implicit Manifold Learning on Generative Adversarial Networks

This paper raises an implicit manifold learning perspective in Generative Adversarial Networks (GANs), by studying how the support of the learned distribution, modelled as a submanifold $\mathcal{M}_{\theta}$, perfectly match with $\mathcal{M}_{r}$, the support of the real data distribution. We show that optimizing Jensen-Shannon divergence forces $\mathcal{M}_{\theta}$ to perfectly match with $\mathcal{M}_{r}$, while optimizing Wasserstein distance does not. On the other hand, by comparing the gradients of the Jensen-Shannon divergence and the Wasserstein distances ($W_1$ and $W_2^2$) in their primal forms, we conjecture that Wasserstein $W_2^2$ may enjoy desirable properties such as reduced mode collapse. It is therefore interesting to design new distances that inherit the best from both distances.