Rethinking Test-time Likelihood: The Likelihood Path Principle and Its Application to OOD Detection

While likelihood is attractive in theory, its estimates by deep generative models (DGMs) are often broken in practice, and perform poorly for out of distribution (OOD) Detection. Various recent works started to consider alternative scores and achieved better performances. However, such recipes do not come with provable guarantees, nor is it clear that their choices extract sufficient information. We attempt to change this by conducting a case study on variational autoencoders (VAEs). First, we introduce the likelihood path (LPath) principle, generalizing the likelihood principle. This narrows the search for informative summary statistics down to the minimal sufficient statistics of VAEs' conditional likelihoods. Second, introducing new theoretic tools such as nearly essential support, essential distance and co-Lipschitzness, we obtain non-asymptotic provable OOD detection guarantees for certain distillation of the minimal sufficient statistics. The corresponding LPath algorithm demonstrates SOTA performances, even using simple and small VAEs with poor likelihood estimates. To our best knowledge, this is the first provable unsupervised OOD method that delivers excellent empirical results, better than any other VAEs based techniques. We use the same model as \cite{xiao2020likelihood}, open sourced from: https://github.com/XavierXiao/Likelihood-Regret

Robust Risk-Sensitive Reinforcement Learning Agents for Trading Markets

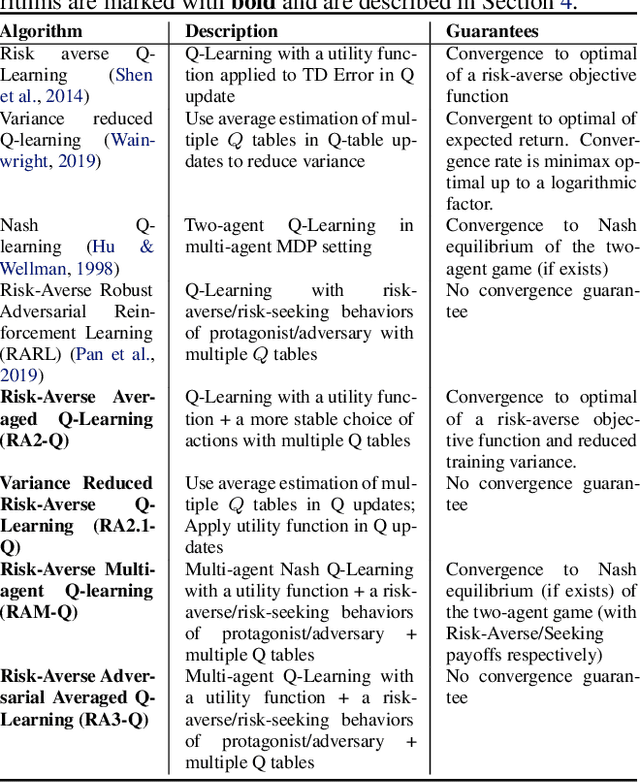
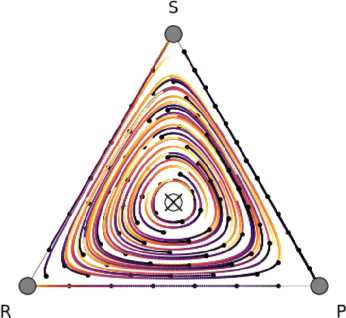
Trading markets represent a real-world financial application to deploy reinforcement learning agents, however, they carry hard fundamental challenges such as high variance and costly exploration. Moreover, markets are inherently a multiagent domain composed of many actors taking actions and changing the environment. To tackle these type of scenarios agents need to exhibit certain characteristics such as risk-awareness, robustness to perturbations and low learning variance. We take those as building blocks and propose a family of four algorithms. First, we contribute with two algorithms that use risk-averse objective functions and variance reduction techniques. Then, we augment the framework to multi-agent learning and assume an adversary which can take over and perturb the learning process. Our third and fourth algorithms perform well under this setting and balance theoretical guarantees with practical use. Additionally, we consider the multi-agent nature of the environment and our work is the first one extending empirical game theory analysis for multi-agent learning by considering risk-sensitive payoffs.

On the Sensitivity of Adversarial Robustness to Input Data Distributions

Neural networks are vulnerable to small adversarial perturbations. Existing literature largely focused on understanding and mitigating the vulnerability of learned models. In this paper, we demonstrate an intriguing phenomenon about the most popular robust training method in the literature, adversarial training: Adversarial robustness, unlike clean accuracy, is sensitive to the input data distribution. Even a semantics-preserving transformations on the input data distribution can cause a significantly different robustness for the adversarial trained model that is both trained and evaluated on the new distribution. Our discovery of such sensitivity on data distribution is based on a study which disentangles the behaviors of clean accuracy and robust accuracy of the Bayes classifier. Empirical investigations further confirm our finding. We construct semantically-identical variants for MNIST and CIFAR10 respectively, and show that standardly trained models achieve comparable clean accuracies on them, but adversarially trained models achieve significantly different robustness accuracies. This counter-intuitive phenomenon indicates that input data distribution alone can affect the adversarial robustness of trained neural networks, not necessarily the tasks themselves. Lastly, we discuss the practical implications on evaluating adversarial robustness, and make initial attempts to understand this complex phenomenon.

Max-Margin Adversarial (MMA) Training: Direct Input Space Margin Maximization through Adversarial Training

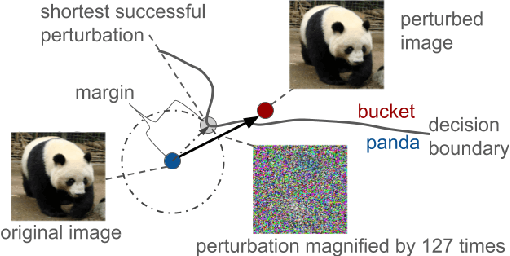
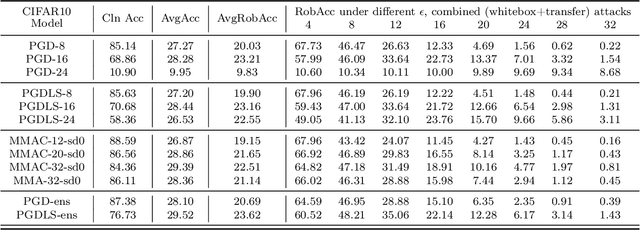
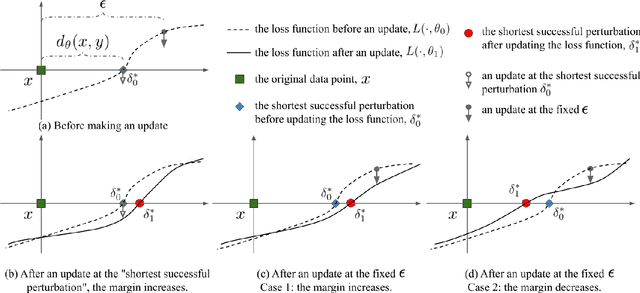
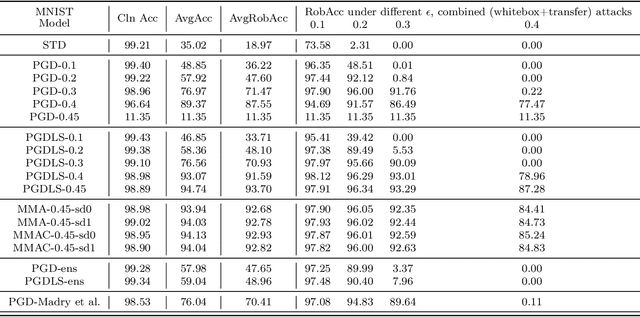
We propose Max-Margin Adversarial (MMA) training for directly maximizing the input space margin. This margin maximization is direct, in the sense that the margin's gradient w.r.t. model parameters can be shown to be parallel with the loss' gradient at the minimal length perturbation, thus gradient ascent on margins can be performed by gradient descent on losses. We further propose a specific formulation of MMA training to maximize the average margin of training examples in order to train models that are robust to adversarial perturbations. It is implemented by performing adversarial training on a novel adaptive norm projected gradient descent (AN-PGD) attack. Preliminary experimental results demonstrate that our method outperforms the existing state of the art methods. In particular, testing against both white-box and transfer projected gradient descent attacks on MNIST, our trained model improves the SOTA $\ell_\infty$ $\epsilon=0.3$ robust accuracy by 2\%, while maintaining the SOTA clean accuracy. Furthermore, the same model provides, to the best of our knowledge, the first model that is robust at $\ell_\infty$ $\epsilon=0.4$, with a robust accuracy of $86.51\%$.

Dimensionality Reduction has Quantifiable Imperfections: Two Geometric Bounds

In this paper, we investigate Dimensionality reduction (DR) maps in an information retrieval setting from a quantitative topology point of view. In particular, we show that no DR maps can achieve perfect precision and perfect recall simultaneously. Thus a continuous DR map must have imperfect precision. We further prove an upper bound on the precision of Lipschitz continuous DR maps. While precision is a natural measure in an information retrieval setting, it does not measure `how' wrong the retrieved data is. We therefore propose a new measure based on Wasserstein distance that comes with similar theoretical guarantee. A key technical step in our proofs is a particular optimization problem of the $L_2$-Wasserstein distance over a constrained set of distributions. We provide a complete solution to this optimization problem, which can be of independent interest on the technical side.

Implicit Manifold Learning on Generative Adversarial Networks

This paper raises an implicit manifold learning perspective in Generative Adversarial Networks (GANs), by studying how the support of the learned distribution, modelled as a submanifold $\mathcal{M}_{\theta}$, perfectly match with $\mathcal{M}_{r}$, the support of the real data distribution. We show that optimizing Jensen-Shannon divergence forces $\mathcal{M}_{\theta}$ to perfectly match with $\mathcal{M}_{r}$, while optimizing Wasserstein distance does not. On the other hand, by comparing the gradients of the Jensen-Shannon divergence and the Wasserstein distances ($W_1$ and $W_2^2$) in their primal forms, we conjecture that Wasserstein $W_2^2$ may enjoy desirable properties such as reduced mode collapse. It is therefore interesting to design new distances that inherit the best from both distances.