Elias Tragas
Scalable Recommender Systems through Recursive Evidence Chains
Jul 05, 2018
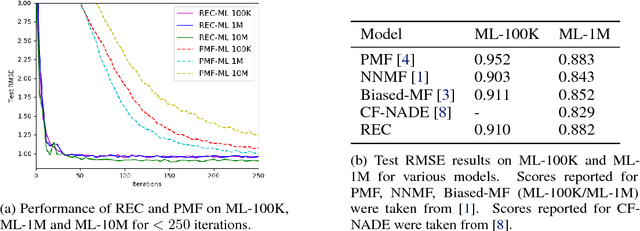
Abstract:Recommender systems can be formulated as a matrix completion problem, predicting ratings from user and item parameter vectors. Optimizing these parameters by subsampling data becomes difficult as the number of users and items grows. We develop a novel approach to generate all latent variables on demand from the ratings matrix itself and a fixed pool of parameters. We estimate missing ratings using chains of evidence that link them to a small set of prototypical users and items. Our model automatically addresses the cold-start and online learning problems by combining information across both users and items. We investigate the scaling behavior of this model, and demonstrate competitive results with respect to current matrix factorization techniques in terms of accuracy and convergence speed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge