Interplay Between Optimization and Generalization of Stochastic Gradient Descent with Covariance Noise

The choice of batch-size in a stochastic optimization algorithm plays a substantial role for both optimization and generalization. Increasing the batch-size used typically improves optimization but degrades generalization. To address the problem of improving generalization while maintaining optimal convergence in large-batch training, we propose to add covariance noise to the gradients. We demonstrate that the optimization performance of our method is more accurately captured by the structure of the noise covariance matrix rather than by the variance of gradients. Moreover, over the convex-quadratic, we prove in theory that it can be characterized by the Frobenius norm of the noise matrix. Our empirical studies with standard deep learning model-architectures and datasets shows that our method not only improves generalization performance in large-batch training, but furthermore, does so in a way where the optimization performance remains desirable and the training duration is not elongated.

A Coordinate-Free Construction of Scalable Natural Gradient

Most neural networks are trained using first-order optimization methods, which are sensitive to the parameterization of the model. Natural gradient descent is invariant to smooth reparameterizations because it is defined in a coordinate-free way, but tractable approximations are typically defined in terms of coordinate systems, and hence may lose the invariance properties. We analyze the invariance properties of the Kronecker-Factored Approximate Curvature (K-FAC) algorithm by constructing the algorithm in a coordinate-free way. We explicitly construct a Riemannian metric under which the natural gradient matches the K-FAC update; invariance to affine transformations of the activations follows immediately. We extend our framework to analyze the invariance properties of K-FAC applied to convolutional networks and recurrent neural networks, as well as metrics other than the usual Fisher metric.

Scalable Recommender Systems through Recursive Evidence Chains

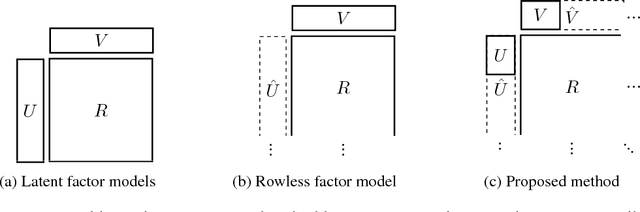
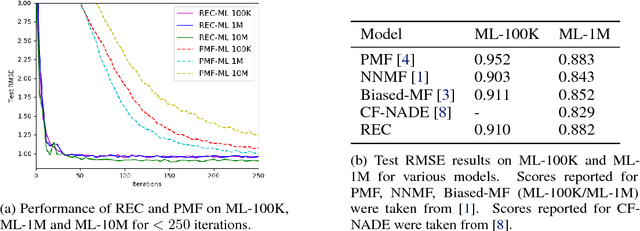
Recommender systems can be formulated as a matrix completion problem, predicting ratings from user and item parameter vectors. Optimizing these parameters by subsampling data becomes difficult as the number of users and items grows. We develop a novel approach to generate all latent variables on demand from the ratings matrix itself and a fixed pool of parameters. We estimate missing ratings using chains of evidence that link them to a small set of prototypical users and items. Our model automatically addresses the cold-start and online learning problems by combining information across both users and items. We investigate the scaling behavior of this model, and demonstrate competitive results with respect to current matrix factorization techniques in terms of accuracy and convergence speed.