Kun Mao
SMARTAPS: Tool-augmented LLMs for Operations Management
Jul 23, 2025Abstract:Large language models (LLMs) present intriguing opportunities to enhance user interaction with traditional algorithms and tools in real-world applications. An advanced planning system (APS) is a sophisticated software that leverages optimization to help operations planners create, interpret, and modify an operational plan. While highly beneficial, many customers are priced out of using an APS due to the ongoing costs of consultants responsible for customization and maintenance. To address the need for a more accessible APS expressed by supply chain planners, we present SmartAPS, a conversational system built on a tool-augmented LLM. Our system provides operations planners with an intuitive natural language chat interface, allowing them to query information, perform counterfactual reasoning, receive recommendations, and execute scenario analysis to better manage their operation. A short video demonstrating the system has been released: https://youtu.be/KtIrJjlDbyw
Fitness Landscape of Large Language Model-Assisted Automated Algorithm Search
May 01, 2025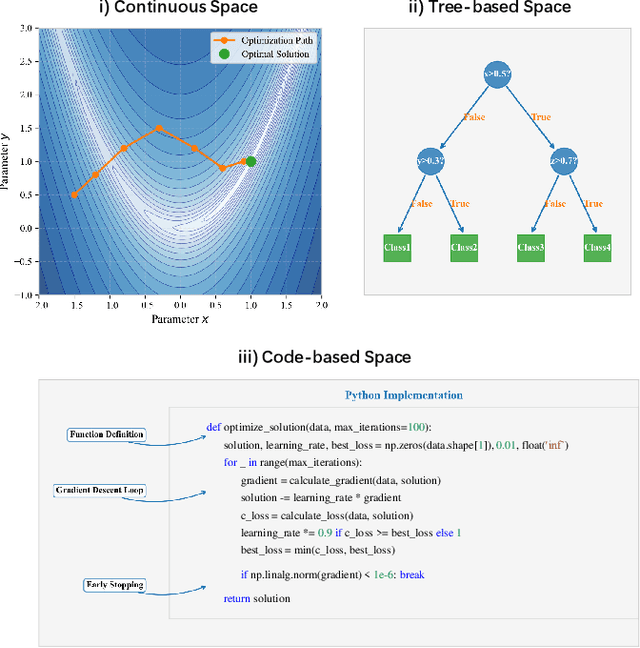
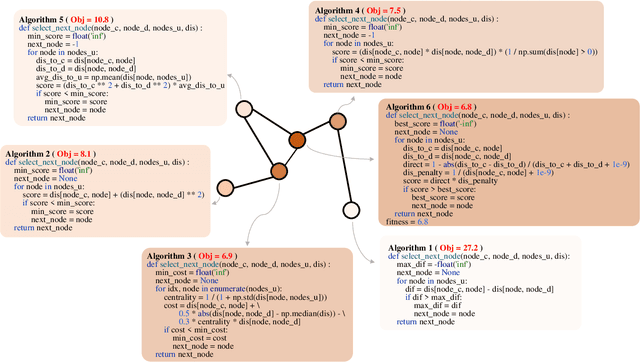
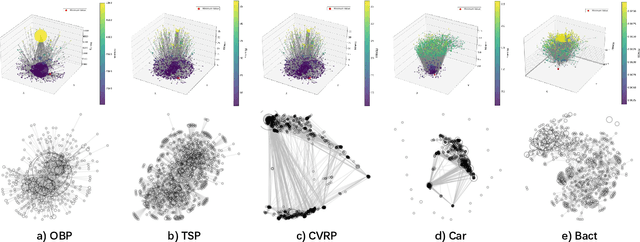
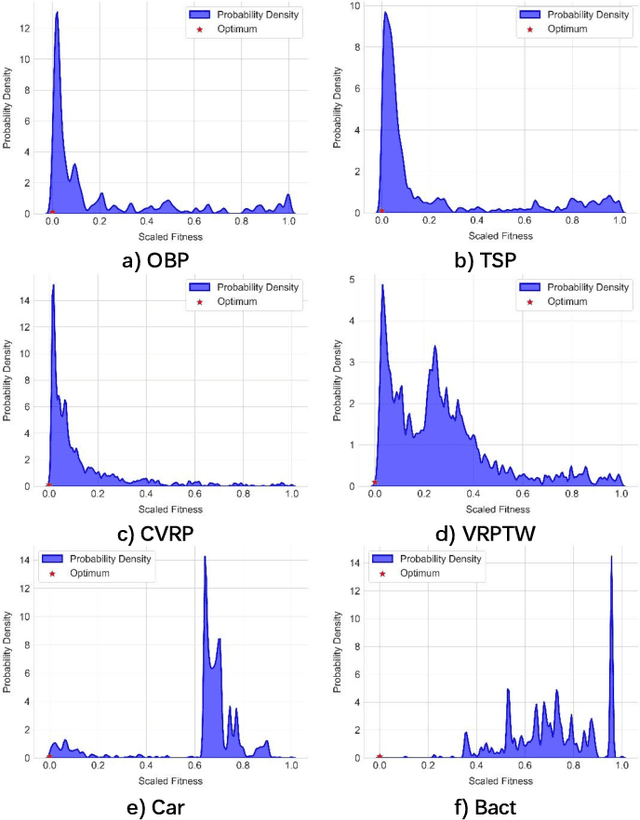
Abstract:Large Language Models (LLMs) have demonstrated significant potential in algorithm design. However, when integrated into search frameworks for iterative algorithm search, the underlying fitness landscape--critical for understanding search behaviou--remains underexplored. In this paper, we illustrate and analyze the fitness landscape of LLM-assisted Algorithm Search (LAS) using a graph-based approach, where nodes represent algorithms and edges denote transitions between them. We conduct extensive evaluations across six algorithm design tasks and six commonly used LLMs. Our findings reveal that LAS landscapes are highly multimodal and rugged, particularly in combinatorial optimization tasks, with distinct structural variations across tasks and LLMs. For instance, heuristic design tasks exhibit dense clusters of high-performing algorithms, while symbolic regression tasks show sparse, scattered distributions. Additionally, we demonstrate how population size influences exploration-exploitation trade-offs and the evolving trajectory of elite algorithms. These insights not only advance our understanding of LAS landscapes but also provide practical guidance for designing more effective LAS methods.
Machine Learning Insides OptVerse AI Solver: Design Principles and Applications
Jan 17, 2024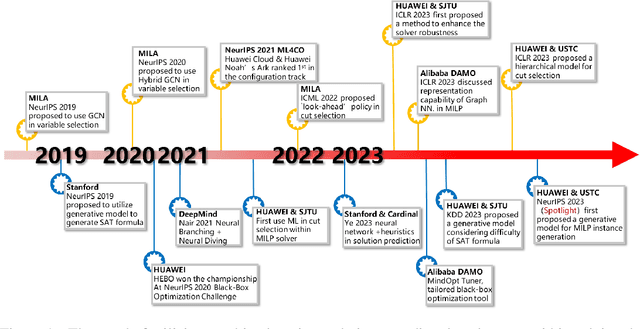
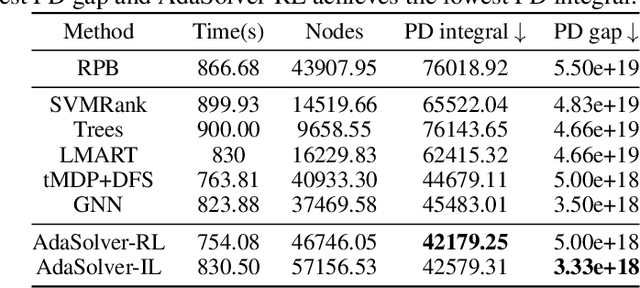

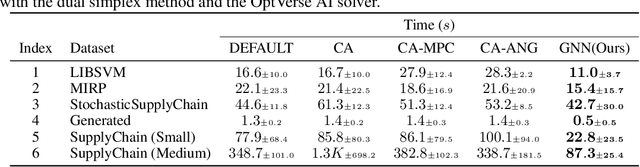
Abstract:In an era of digital ubiquity, efficient resource management and decision-making are paramount across numerous industries. To this end, we present a comprehensive study on the integration of machine learning (ML) techniques into Huawei Cloud's OptVerse AI Solver, which aims to mitigate the scarcity of real-world mathematical programming instances, and to surpass the capabilities of traditional optimization techniques. We showcase our methods for generating complex SAT and MILP instances utilizing generative models that mirror multifaceted structures of real-world problem. Furthermore, we introduce a training framework leveraging augmentation policies to maintain solvers' utility in dynamic environments. Besides the data generation and augmentation, our proposed approaches also include novel ML-driven policies for personalized solver strategies, with an emphasis on applications like graph convolutional networks for initial basis selection and reinforcement learning for advanced presolving and cut selection. Additionally, we detail the incorporation of state-of-the-art parameter tuning algorithms which markedly elevate solver performance. Compared with traditional solvers such as Cplex and SCIP, our ML-augmented OptVerse AI Solver demonstrates superior speed and precision across both established benchmarks and real-world scenarios, reinforcing the practical imperative and effectiveness of machine learning techniques in mathematical programming solvers.
Learning to Reformulate for Linear Programming
Jan 17, 2022

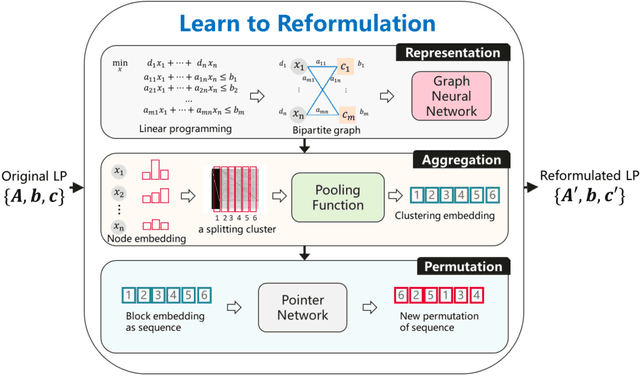
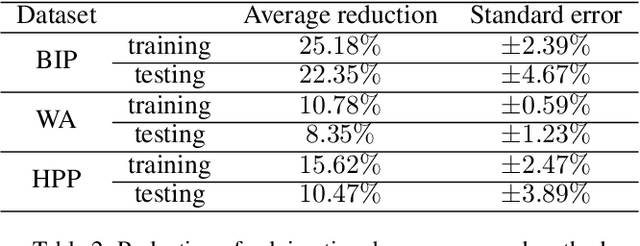
Abstract:It has been verified that the linear programming (LP) is able to formulate many real-life optimization problems, which can obtain the optimum by resorting to corresponding solvers such as OptVerse, Gurobi and CPLEX. In the past decades, a serial of traditional operation research algorithms have been proposed to obtain the optimum of a given LP in a fewer solving time. Recently, there is a trend of using machine learning (ML) techniques to improve the performance of above solvers. However, almost no previous work takes advantage of ML techniques to improve the performance of solver from the front end, i.e., the modeling (or formulation). In this paper, we are the first to propose a reinforcement learning-based reformulation method for LP to improve the performance of solving process. Using an open-source solver COIN-OR LP (CLP) as an environment, we implement the proposed method over two public research LP datasets and one large-scale LP dataset collected from practical production planning scenario. The evaluation results suggest that the proposed method can effectively reduce both the solving iteration number ($25\%\downarrow$) and the solving time ($15\%\downarrow$) over above datasets in average, compared to directly solving the original LP instances.
An Improved Reinforcement Learning Algorithm for Learning to Branch
Jan 17, 2022Abstract:Most combinatorial optimization problems can be formulated as mixed integer linear programming (MILP), in which branch-and-bound (B\&B) is a general and widely used method. Recently, learning to branch has become a hot research topic in the intersection of machine learning and combinatorial optimization. In this paper, we propose a novel reinforcement learning-based B\&B algorithm. Similar to offline reinforcement learning, we initially train on the demonstration data to accelerate learning massively. With the improvement of the training effect, the agent starts to interact with the environment with its learned policy gradually. It is critical to improve the performance of the algorithm by determining the mixing ratio between demonstration and self-generated data. Thus, we propose a prioritized storage mechanism to control this ratio automatically. In order to improve the robustness of the training process, a superior network is additionally introduced based on Double DQN, which always serves as a Q-network with competitive performance. We evaluate the performance of the proposed algorithm over three public research benchmarks and compare it against strong baselines, including three classical heuristics and one state-of-the-art imitation learning-based branching algorithm. The results show that the proposed algorithm achieves the best performance among compared algorithms and possesses the potential to improve B\&B algorithm performance continuously.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge