Retire: Robust Expectile Regression in High Dimensions

High-dimensional data can often display heterogeneity due to heteroscedastic variance or inhomogeneous covariate effects. Penalized quantile and expectile regression methods offer useful tools to detect heteroscedasticity in high-dimensional data. The former is computationally challenging due to the non-smooth nature of the check loss, and the latter is sensitive to heavy-tailed error distributions. In this paper, we propose and study (penalized) robust expectile regression (retire), with a focus on iteratively reweighted $\ell_1$-penalization which reduces the estimation bias from $\ell_1$-penalization and leads to oracle properties. Theoretically, we establish the statistical properties of the retire estimator under two regimes: (i) low-dimensional regime in which $d \ll n$; (ii) high-dimensional regime in which $s\ll n\ll d$ with $s$ denoting the number of significant predictors. In the high-dimensional setting, we carefully characterize the solution path of the iteratively reweighted $\ell_1$-penalized retire estimation, adapted from the local linear approximation algorithm for folded-concave regularization. Under a mild minimum signal strength condition, we show that after as many as $\log(\log d)$ iterations the final iterate enjoys the oracle convergence rate. At each iteration, the weighted $\ell_1$-penalized convex program can be efficiently solved by a semismooth Newton coordinate descent algorithm. Numerical studies demonstrate the competitive performance of the proposed procedure compared with either non-robust or quantile regression based alternatives.

Communication-Efficient Distributed Quantile Regression with Optimal Statistical Guarantees

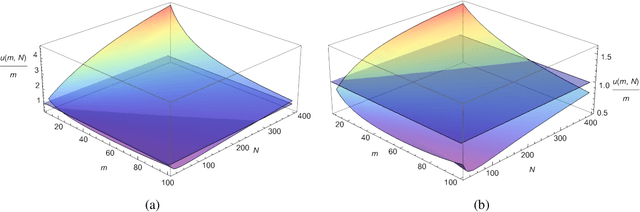
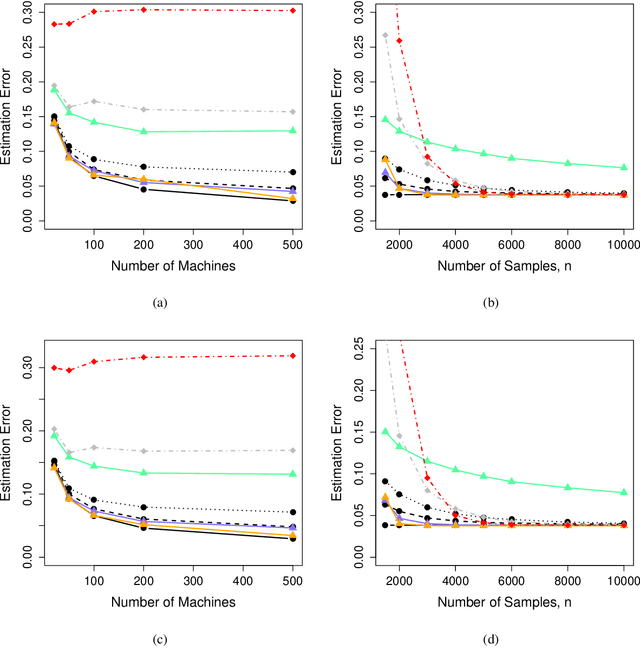
We address the problem of how to achieve optimal inference in distributed quantile regression without stringent scaling conditions. This is challenging due to the non-smooth nature of the quantile regression loss function, which invalidates the use of existing methodology. The difficulties are resolved through a double-smoothing approach that is applied to the local (at each data source) and global objective functions. Despite the reliance on a delicate combination of local and global smoothing parameters, the quantile regression model is fully parametric, thereby facilitating interpretation. In the low-dimensional regime, we discuss and compare several alternative confidence set constructions, based on inversion of Wald and score-type tests and resam-pling techniques, detailing an improvement that is effective for more extreme quantile coefficients. In high dimensions, a sparse framework is adopted, where the proposed doubly-smoothed objective function is complemented with an $\ell_1$-penalty. A thorough simulation study further elucidates our findings. Finally, we provide estimation theory and numerical studies for sparse quantile regression in the high-dimensional setting.

Model Linkage Selection for Cooperative Learning

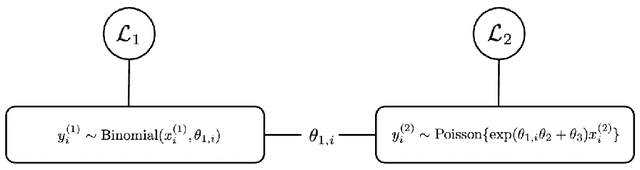
Rapid developments in data collecting devices and computation platforms produce an emerging number of learners and data modalities in many scientific domains. We consider the setting in which each learner holds a pair of parametric statistical model and a specific data source, with the goal of integrating information across a set of learners to enhance the prediction accuracy of a specific learner. One natural way to integrate information is to build a joint model across a set of learners that shares common parameters of interest. However, the parameter sharing patterns across a set of learners are not known a priori. Misspecifying the parameter sharing patterns and the parametric statistical model for each learner yields a biased estimator and degrades the prediction accuracy of the joint model. In this paper, we propose a novel framework for integrating information across a set of learners that is robust against model misspecification and misspecified parameter sharing patterns. The main crux is to sequentially incorporates additional learners that can enhance the prediction accuracy of an existing joint model based on a user-specified parameter sharing patterns across a set of learners, starting from a model with one learner. Theoretically, we show that the proposed method can data-adaptively select the correct parameter sharing patterns based on a user-specified parameter sharing patterns, and thus enhances the prediction accuracy of a learner. Extensive numerical studies are performed to evaluate the performance of the proposed method.

Estimating and Inferring the Maximum Degree of Stimulus-Locked Time-Varying Brain Connectivity Networks

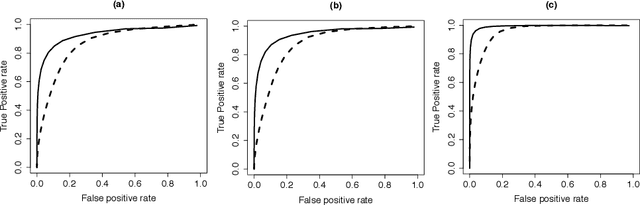
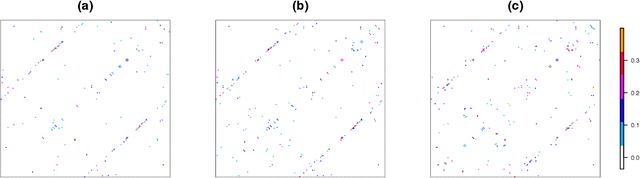
Neuroscientists have enjoyed much success in understanding brain functions by constructing brain connectivity networks using data collected under highly controlled experimental settings. However, these experimental settings bear little resemblance to our real-life experience in day-to-day interactions with the surroundings. To address this issue, neuroscientists have been measuring brain activity under natural viewing experiments in which the subjects are given continuous stimuli, such as watching a movie or listening to a story. The main challenge with this approach is that the measured signal consists of both the stimulus-induced signal, as well as intrinsic-neural and non-neuronal signals. By exploiting the experimental design, we propose to estimate stimulus-locked brain network by treating non-stimulus-induced signals as nuisance parameters. In many neuroscience applications, it is often important to identify brain regions that are connected to many other brain regions during cognitive process. We propose an inferential method to test whether the maximum degree of the estimated network is larger than a pre-specific number. We prove that the type I error can be controlled and that the power increases to one asymptotically. Simulation studies are conducted to assess the performance of our method. Finally, we analyze a functional magnetic resonance imaging dataset obtained under the Sherlock Holmes movie stimuli.

Distributionally Robust Reduced Rank Regression and Principal Component Analysis in High Dimensions

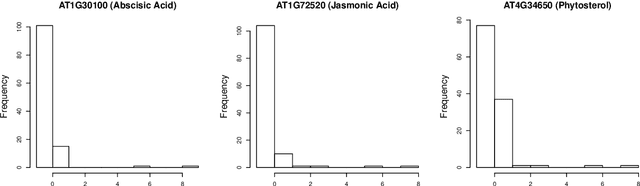
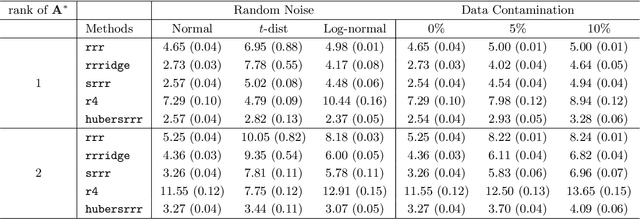
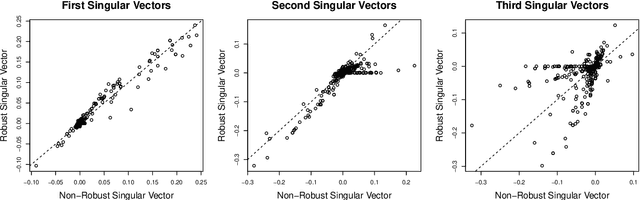
We propose robust sparse reduced rank regression and robust sparse principal component analysis for analyzing large and complex high-dimensional data with heavy-tailed random noise. The proposed methods are based on convex relaxations of rank-and sparsity-constrained non-convex optimization problems, which are solved using the alternating direction method of multipliers (ADMM) algorithm. For robust sparse reduced rank regression, we establish non-asymptotic estimation error bounds under both Frobenius and nuclear norms, while existing results focus mostly on rank-selection and prediction consistency. Our theoretical results quantify the tradeoff between heavy-tailedness of the random noise and statistical bias. For random noise with bounded $(1+\delta)$th moment with $\delta \in (0,1)$, the rate of convergence is a function of $\delta$, and is slower than the sub-Gaussian-type deviation bounds; for random noise with bounded second moment, we recover the results obtained under sub-Gaussian noise. Furthermore, the transition between the two regimes is smooth. For robust sparse principal component analysis, we propose to truncate the observed data, and show that this truncation will lead to consistent estimation of the eigenvectors. We then establish theoretical results similar to those of robust sparse reduced rank regression. We illustrate the performance of these methods via extensive numerical studies and two real data applications.

A convex formulation for high-dimensional sparse sliced inverse regression

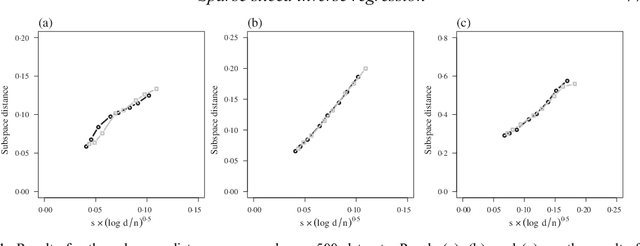
Sliced inverse regression is a popular tool for sufficient dimension reduction, which replaces covariates with a minimal set of their linear combinations without loss of information on the conditional distribution of the response given the covariates. The estimated linear combinations include all covariates, making results difficult to interpret and perhaps unnecessarily variable, particularly when the number of covariates is large. In this paper, we propose a convex formulation for fitting sparse sliced inverse regression in high dimensions. Our proposal estimates the subspace of the linear combinations of the covariates directly and performs variable selection simultaneously. We solve the resulting convex optimization problem via the linearized alternating direction methods of multiplier algorithm, and establish an upper bound on the subspace distance between the estimated and the true subspaces. Through numerical studies, we show that our proposal is able to identify the correct covariates in the high-dimensional setting.

Local Uncertainty Sampling for Large-Scale Multi-Class Logistic Regression

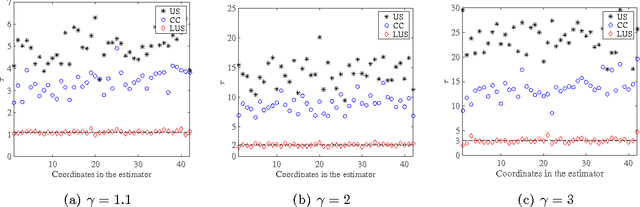
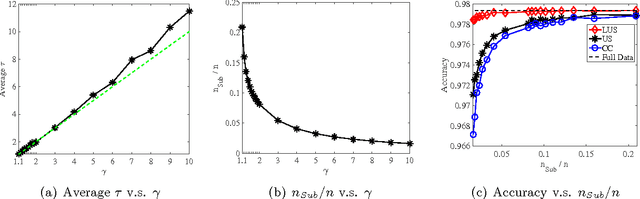
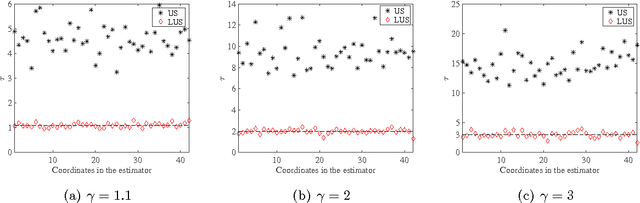
A major challenge for building statistical models in the big data era is that the available data volume far exceeds the computational capability. A common approach for solving this problem is to employ a subsampled dataset that can be handled by available computational resources. In this paper, we propose a general subsampling scheme for large-scale multi-class logistic regression and examine the variance of the resulting estimator. We show that asymptotically, the proposed method always achieves a smaller variance than that of the uniform random sampling. Moreover, when the classes are conditionally imbalanced, significant improvement over uniform sampling can be achieved. Empirical performance of the proposed method is compared to other methods on both simulated and real-world datasets, and these results match and confirm our theoretical analysis.

Sparse Generalized Eigenvalue Problem: Optimal Statistical Rates via Truncated Rayleigh Flow

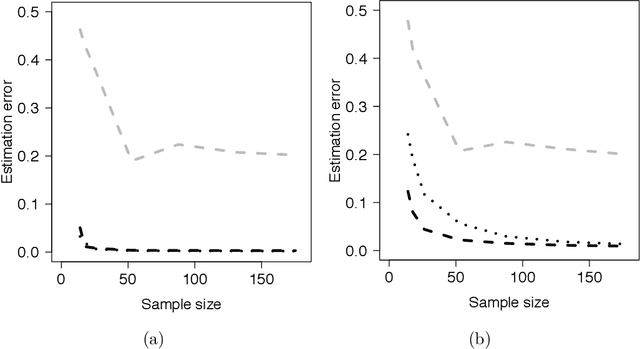
Sparse generalized eigenvalue problem (GEP) plays a pivotal role in a large family of high-dimensional statistical models, including sparse Fisher's discriminant analysis, canonical correlation analysis, and sufficient dimension reduction. Sparse GEP involves solving a non-convex optimization problem. Most existing methods and theory in the context of specific statistical models that are special cases of the sparse GEP require restrictive structural assumptions on the input matrices. In this paper, we propose a two-stage computational framework to solve the sparse GEP. At the first stage, we solve a convex relaxation of the sparse GEP. Taking the solution as an initial value, we then exploit a nonconvex optimization perspective and propose the truncated Rayleigh flow method (Rifle) to estimate the leading generalized eigenvector. We show that Rifle converges linearly to a solution with the optimal statistical rate of convergence for many statistical models. Theoretically, our method significantly improves upon the existing literature by eliminating structural assumptions on the input matrices for both stages. To achieve this, our analysis involves two key ingredients: (i) a new analysis of the gradient based method on nonconvex objective functions, and (ii) a fine-grained characterization of the evolution of sparsity patterns along the solution path. Thorough numerical studies are provided to validate the theoretical results.

Graphical Nonconvex Optimization for Optimal Estimation in Gaussian Graphical Models

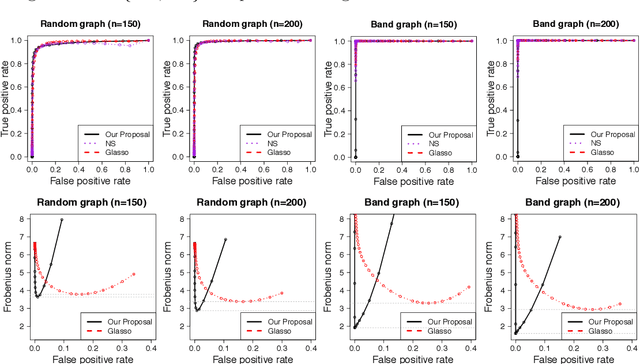
We consider the problem of learning high-dimensional Gaussian graphical models. The graphical lasso is one of the most popular methods for estimating Gaussian graphical models. However, it does not achieve the oracle rate of convergence. In this paper, we propose the graphical nonconvex optimization for optimal estimation in Gaussian graphical models, which is then approximated by a sequence of convex programs. Our proposal is computationally tractable and produces an estimator that achieves the oracle rate of convergence. The statistical error introduced by the sequential approximation using the convex programs are clearly demonstrated via a contraction property. The rate of convergence can be further improved using the notion of sparsity pattern. The proposed methodology is then extended to semiparametric graphical models. We show through numerical studies that the proposed estimator outperforms other popular methods for estimating Gaussian graphical models.

Selection Bias Correction and Effect Size Estimation under Dependence

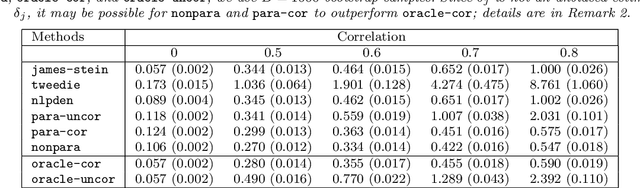
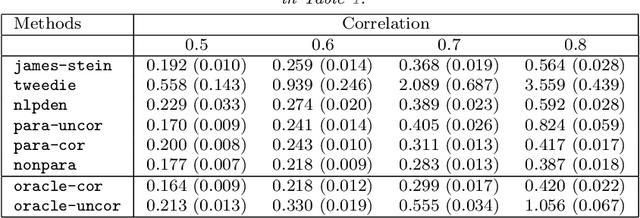
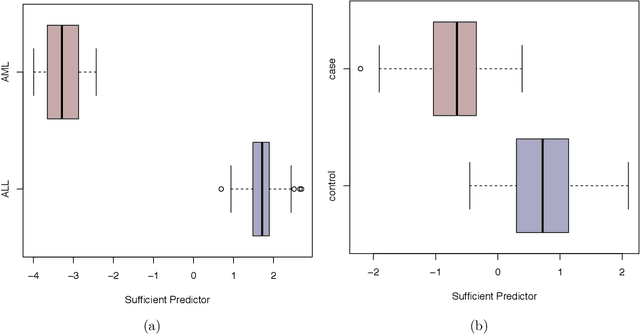
We consider large-scale studies in which it is of interest to test a very large number of hypotheses, and then to estimate the effect sizes corresponding to the rejected hypotheses. For instance, this setting arises in the analysis of gene expression or DNA sequencing data. However, naive estimates of the effect sizes suffer from selection bias, i.e., some of the largest naive estimates are large due to chance alone. Many authors have proposed methods to reduce the effects of selection bias under the assumption that the naive estimates of the effect sizes are independent. Unfortunately, when the effect size estimates are dependent, these existing techniques can have very poor performance, and in practice there will often be dependence. We propose an estimator that adjusts for selection bias under a recently-proposed frequentist framework, without the independence assumption. We study some properties of the proposed estimator, and illustrate that it outperforms past proposals in a simulation study and on two gene expression data sets.