Sparse Generalized Eigenvalue Problem: Optimal Statistical Rates via Truncated Rayleigh Flow
Paper and Code
Aug 31, 2018
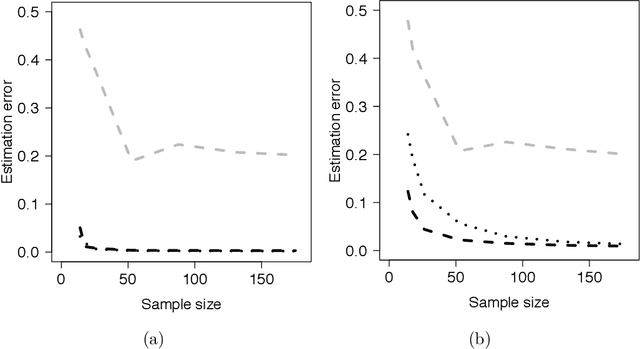
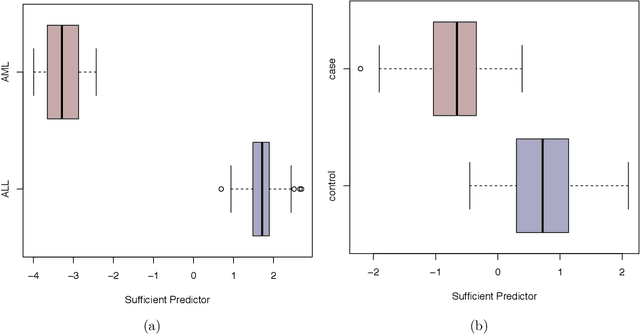
Sparse generalized eigenvalue problem (GEP) plays a pivotal role in a large family of high-dimensional statistical models, including sparse Fisher's discriminant analysis, canonical correlation analysis, and sufficient dimension reduction. Sparse GEP involves solving a non-convex optimization problem. Most existing methods and theory in the context of specific statistical models that are special cases of the sparse GEP require restrictive structural assumptions on the input matrices. In this paper, we propose a two-stage computational framework to solve the sparse GEP. At the first stage, we solve a convex relaxation of the sparse GEP. Taking the solution as an initial value, we then exploit a nonconvex optimization perspective and propose the truncated Rayleigh flow method (Rifle) to estimate the leading generalized eigenvector. We show that Rifle converges linearly to a solution with the optimal statistical rate of convergence for many statistical models. Theoretically, our method significantly improves upon the existing literature by eliminating structural assumptions on the input matrices for both stages. To achieve this, our analysis involves two key ingredients: (i) a new analysis of the gradient based method on nonconvex objective functions, and (ii) a fine-grained characterization of the evolution of sparsity patterns along the solution path. Thorough numerical studies are provided to validate the theoretical results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge