Heather Battey
Communication-Efficient Distributed Quantile Regression with Optimal Statistical Guarantees
Oct 25, 2021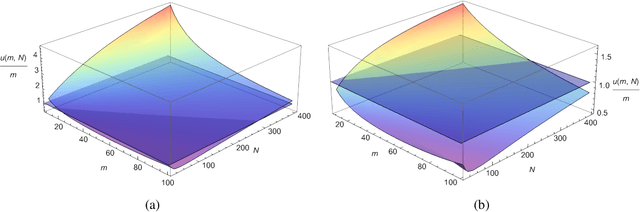

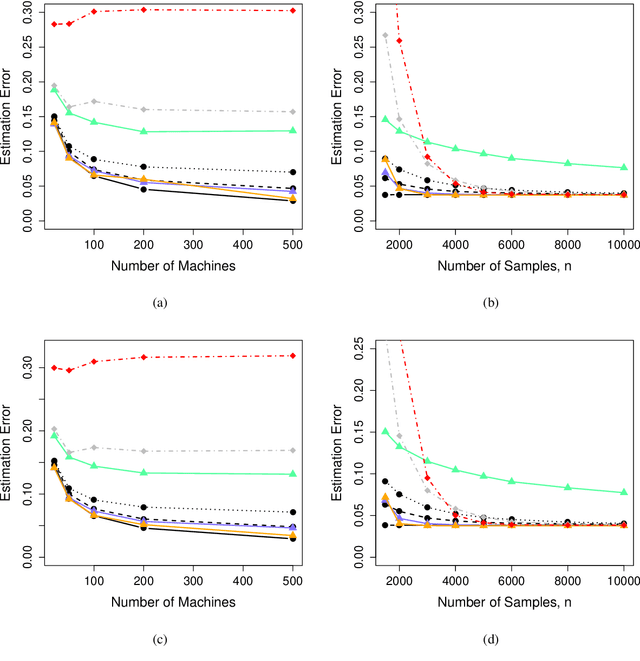

Abstract:We address the problem of how to achieve optimal inference in distributed quantile regression without stringent scaling conditions. This is challenging due to the non-smooth nature of the quantile regression loss function, which invalidates the use of existing methodology. The difficulties are resolved through a double-smoothing approach that is applied to the local (at each data source) and global objective functions. Despite the reliance on a delicate combination of local and global smoothing parameters, the quantile regression model is fully parametric, thereby facilitating interpretation. In the low-dimensional regime, we discuss and compare several alternative confidence set constructions, based on inversion of Wald and score-type tests and resam-pling techniques, detailing an improvement that is effective for more extreme quantile coefficients. In high dimensions, a sparse framework is adopted, where the proposed doubly-smoothed objective function is complemented with an $\ell_1$-penalty. A thorough simulation study further elucidates our findings. Finally, we provide estimation theory and numerical studies for sparse quantile regression in the high-dimensional setting.
An Unethical Optimization Principle
Nov 12, 2019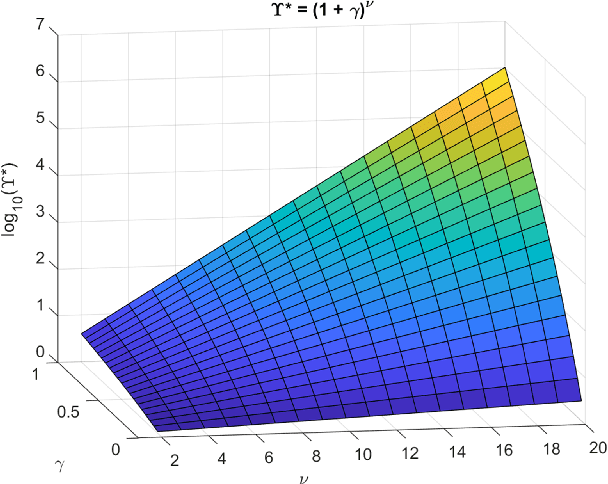
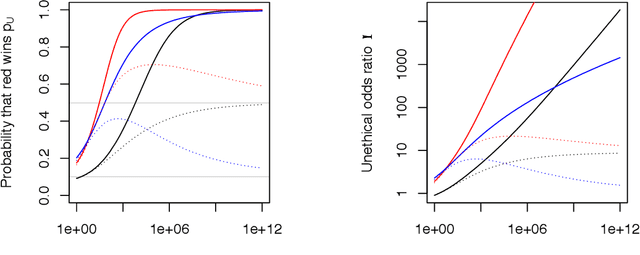
Abstract:If an artificial intelligence aims to maximise risk-adjusted return, then under mild conditions it is disproportionately likely to pick an unethical strategy unless the objective function allows sufficiently for this risk. Even if the proportion ${\eta}$ of available unethical strategies is small, the probability ${p_U}$ of picking an unethical strategy can become large; indeed unless returns are fat-tailed ${p_U}$ tends to unity as the strategy space becomes large. We define an Unethical Odds Ratio Upsilon (${\Upsilon}$) that allows us to calculate ${p_U}$ from ${\eta}$, and we derive a simple formula for the limit of ${\Upsilon}$ as the strategy space becomes large. We give an algorithm for estimating ${\Upsilon}$ and ${p_U}$ in finite cases and discuss how to deal with infinite strategy spaces. We show how this principle can be used to help detect unethical strategies and to estimate ${\eta}$. Finally we sketch some policy implications of this work.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge