An Unethical Optimization Principle
Paper and Code
Nov 12, 2019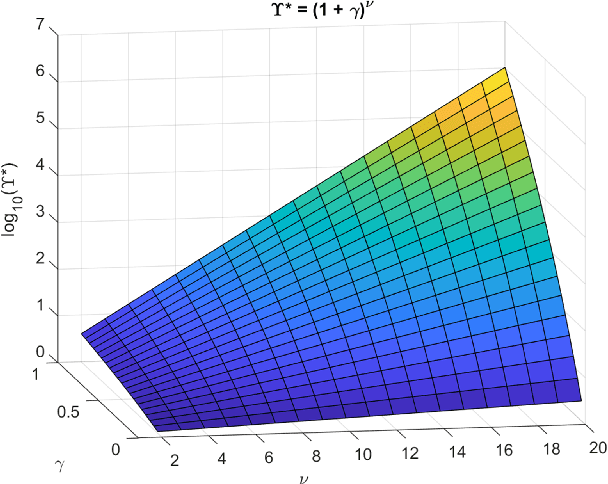
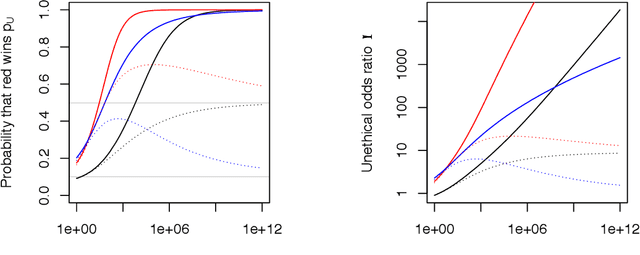
If an artificial intelligence aims to maximise risk-adjusted return, then under mild conditions it is disproportionately likely to pick an unethical strategy unless the objective function allows sufficiently for this risk. Even if the proportion ${\eta}$ of available unethical strategies is small, the probability ${p_U}$ of picking an unethical strategy can become large; indeed unless returns are fat-tailed ${p_U}$ tends to unity as the strategy space becomes large. We define an Unethical Odds Ratio Upsilon (${\Upsilon}$) that allows us to calculate ${p_U}$ from ${\eta}$, and we derive a simple formula for the limit of ${\Upsilon}$ as the strategy space becomes large. We give an algorithm for estimating ${\Upsilon}$ and ${p_U}$ in finite cases and discuss how to deal with infinite strategy spaces. We show how this principle can be used to help detect unethical strategies and to estimate ${\eta}$. Finally we sketch some policy implications of this work.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge