Bayesian nonparametric mixture inconsistency for the number of components: How worried should we be in practice?

We consider the Bayesian mixture of finite mixtures (MFMs) and Dirichlet process mixture (DPM) models for clustering. Recent asymptotic theory has established that DPMs overestimate the number of clusters for large samples and that estimators from both classes of models are inconsistent for the number of clusters under misspecification, but the implications for finite sample analyses are unclear. The final reported estimate after fitting these models is often a single representative clustering obtained using an MCMC summarisation technique, but it is unknown how well such a summary estimates the number of clusters. Here we investigate these practical considerations through simulations and an application to gene expression data, and find that (i) DPMs overestimate the number of clusters even in finite samples, but only to a limited degree that may be correctable using appropriate summaries, and (ii) misspecification can lead to considerable overestimation of the number of clusters in both DPMs and MFMs, but results are nevertheless often still interpretable. We provide recommendations on MCMC summarisation and suggest that although the more appealing asymptotic properties of MFMs provide strong motivation to prefer them, results obtained using MFMs and DPMs are often very similar in practice.

An Unethical Optimization Principle

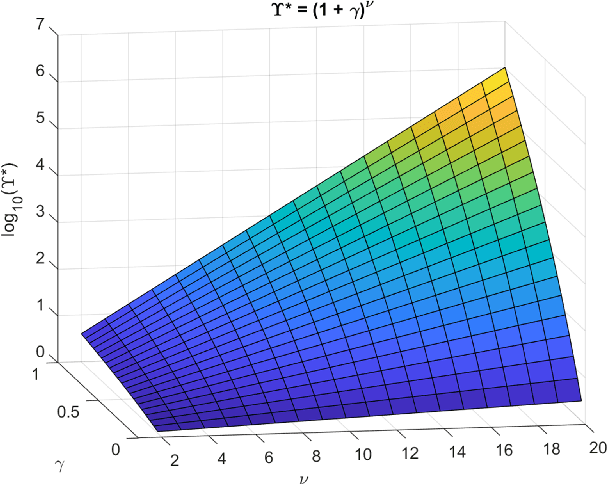
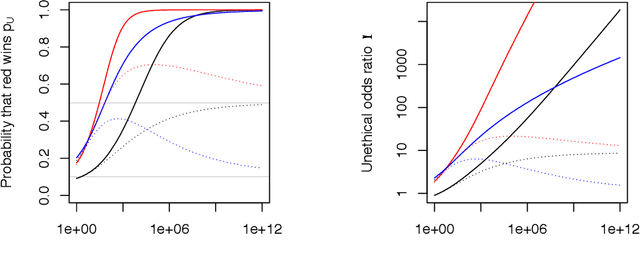
If an artificial intelligence aims to maximise risk-adjusted return, then under mild conditions it is disproportionately likely to pick an unethical strategy unless the objective function allows sufficiently for this risk. Even if the proportion ${\eta}$ of available unethical strategies is small, the probability ${p_U}$ of picking an unethical strategy can become large; indeed unless returns are fat-tailed ${p_U}$ tends to unity as the strategy space becomes large. We define an Unethical Odds Ratio Upsilon (${\Upsilon}$) that allows us to calculate ${p_U}$ from ${\eta}$, and we derive a simple formula for the limit of ${\Upsilon}$ as the strategy space becomes large. We give an algorithm for estimating ${\Upsilon}$ and ${p_U}$ in finite cases and discuss how to deal with infinite strategy spaces. We show how this principle can be used to help detect unethical strategies and to estimate ${\eta}$. Finally we sketch some policy implications of this work.

Fast Automatic Smoothing for Generalized Additive Models

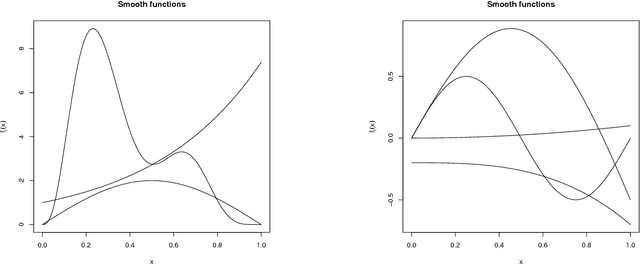
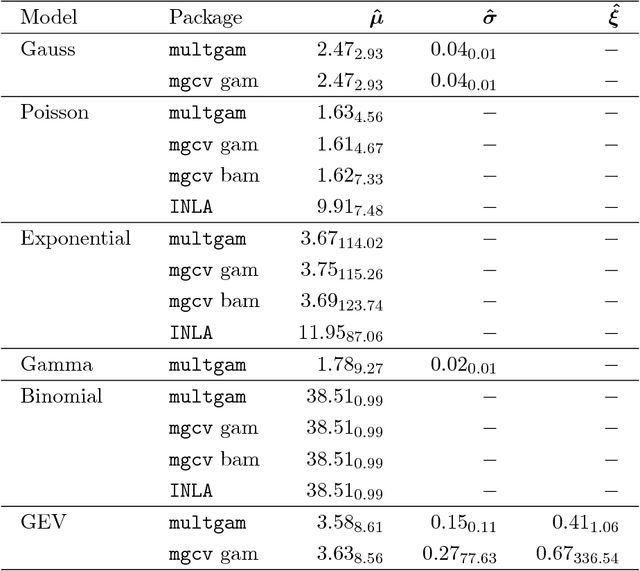
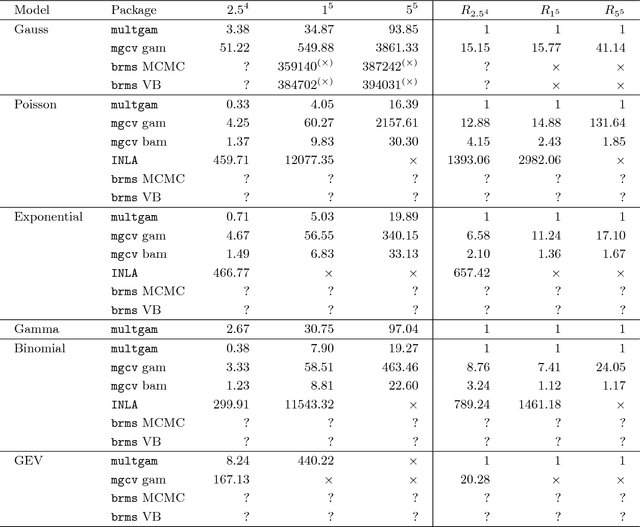
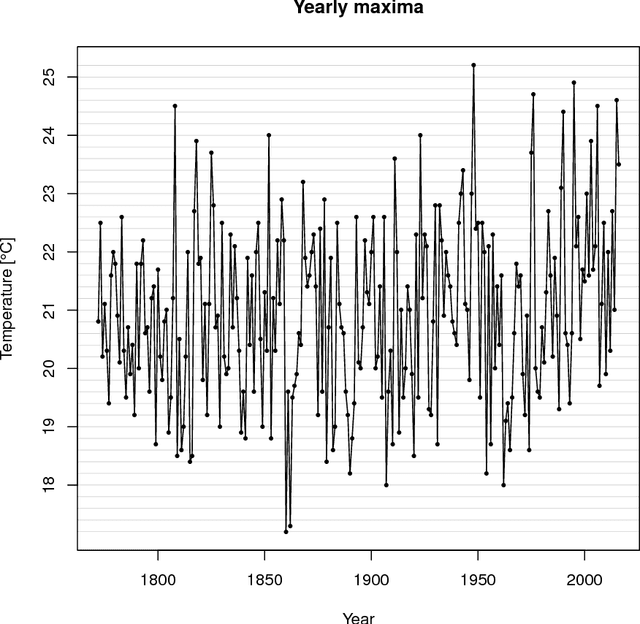
Multiple generalized additive models (GAMs) are a type of distributional regression wherein parameters of probability distributions depend on predictors through smooth functions, with selection of the degree of smoothness via $L_2$ regularization. Multiple GAMs allow finer statistical inference by incorporating explanatory information in any or all of the parameters of the distribution. Owing to their nonlinearity, flexibility and interpretability, GAMs are widely used, but reliable and fast methods for automatic smoothing in large datasets are still lacking, despite recent advances. We develop a general methodology for automatically learning the optimal degree of $L_2$ regularization for multiple GAMs using an empirical Bayes approach. The smooth functions are penalized by different amounts, which are learned simultaneously by maximization of a marginal likelihood through an approximate expectation-maximization algorithm that involves a double Laplace approximation at the E-step, and leads to an efficient M-step. Empirical analysis shows that the resulting algorithm is numerically stable, faster than all existing methods and achieves state-of-the-art accuracy. For illustration, we apply it to an important and challenging problem in the analysis of extremal data.