Yousra El-Bachir
Fast Automatic Smoothing for Generalized Additive Models
Sep 25, 2018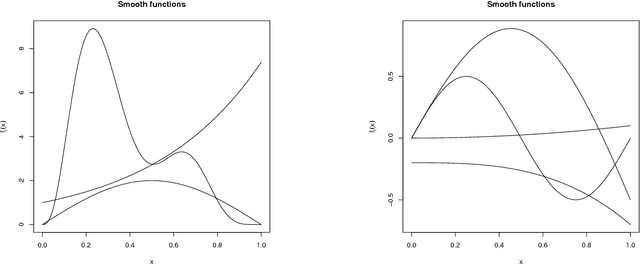
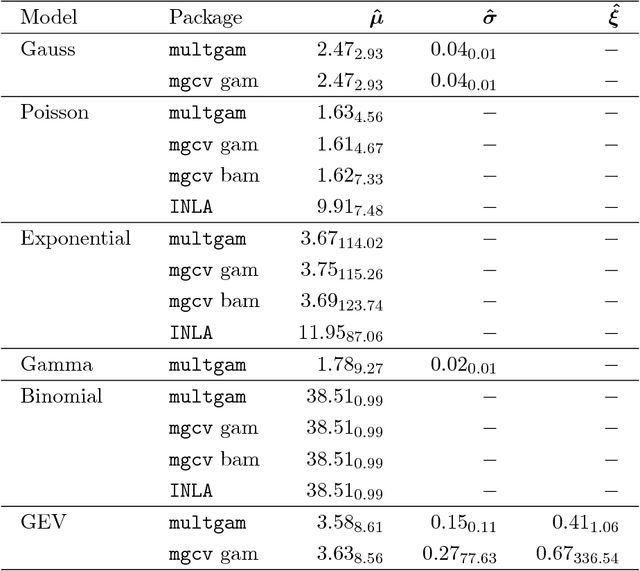
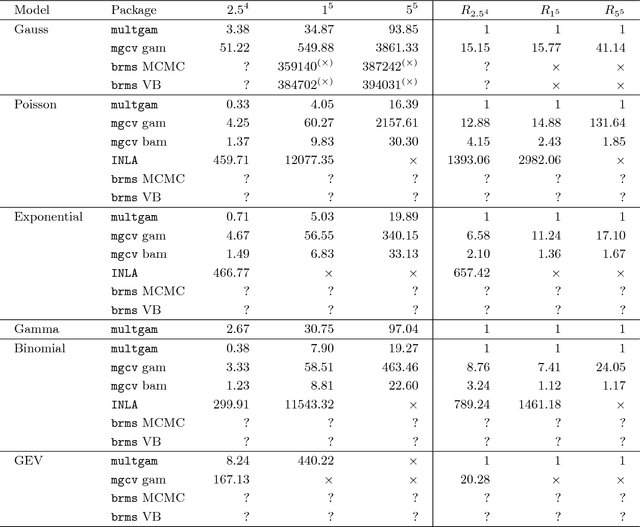
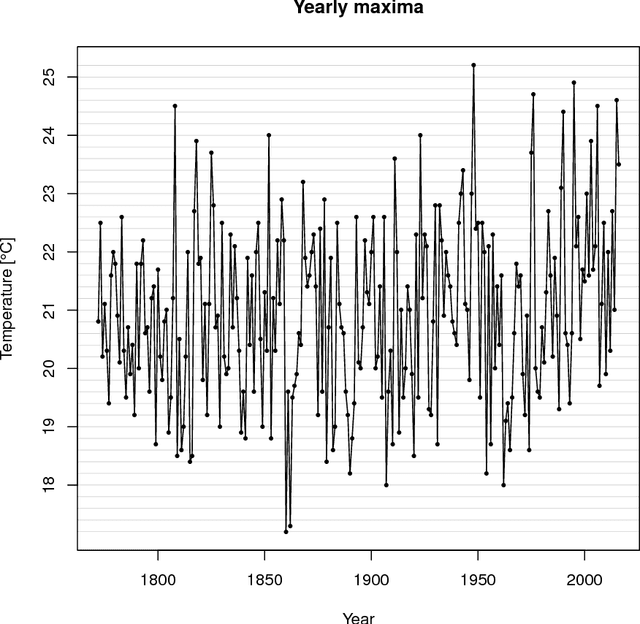
Abstract:Multiple generalized additive models (GAMs) are a type of distributional regression wherein parameters of probability distributions depend on predictors through smooth functions, with selection of the degree of smoothness via $L_2$ regularization. Multiple GAMs allow finer statistical inference by incorporating explanatory information in any or all of the parameters of the distribution. Owing to their nonlinearity, flexibility and interpretability, GAMs are widely used, but reliable and fast methods for automatic smoothing in large datasets are still lacking, despite recent advances. We develop a general methodology for automatically learning the optimal degree of $L_2$ regularization for multiple GAMs using an empirical Bayes approach. The smooth functions are penalized by different amounts, which are learned simultaneously by maximization of a marginal likelihood through an approximate expectation-maximization algorithm that involves a double Laplace approximation at the E-step, and leads to an efficient M-step. Empirical analysis shows that the resulting algorithm is numerically stable, faster than all existing methods and achieves state-of-the-art accuracy. For illustration, we apply it to an important and challenging problem in the analysis of extremal data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge