An Unethical Optimization Principle

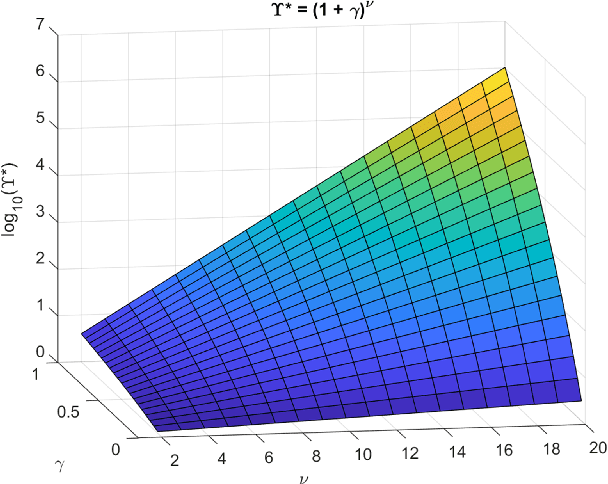
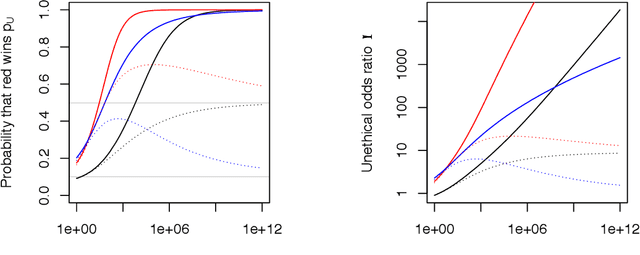
If an artificial intelligence aims to maximise risk-adjusted return, then under mild conditions it is disproportionately likely to pick an unethical strategy unless the objective function allows sufficiently for this risk. Even if the proportion ${\eta}$ of available unethical strategies is small, the probability ${p_U}$ of picking an unethical strategy can become large; indeed unless returns are fat-tailed ${p_U}$ tends to unity as the strategy space becomes large. We define an Unethical Odds Ratio Upsilon (${\Upsilon}$) that allows us to calculate ${p_U}$ from ${\eta}$, and we derive a simple formula for the limit of ${\Upsilon}$ as the strategy space becomes large. We give an algorithm for estimating ${\Upsilon}$ and ${p_U}$ in finite cases and discuss how to deal with infinite strategy spaces. We show how this principle can be used to help detect unethical strategies and to estimate ${\eta}$. Finally we sketch some policy implications of this work.

Inference of modes for linear stochastic processes

For dynamical systems that can be modelled as asymptotically stable linear systems forced by Gaussian noise, this paper develops methods to infer or estimate their modes from observations in real time. The modes can be real or complex. For a real mode, we wish to infer its damping rate and mode shape. For a complex mode, we wish to infer its frequency, damping rate and (complex) mode shape. Their amplitudes and correlations are encoded in a mode covariance matrix. The work is motivated and illustrated by the problem of detection of oscillations in power flow in AC electrical networks. Suggestions of other applications are given.