Communication-Efficient Distributed Quantile Regression with Optimal Statistical Guarantees
Paper and Code
Oct 25, 2021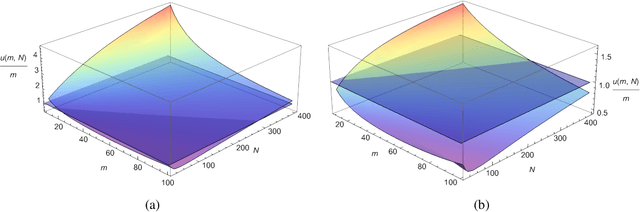

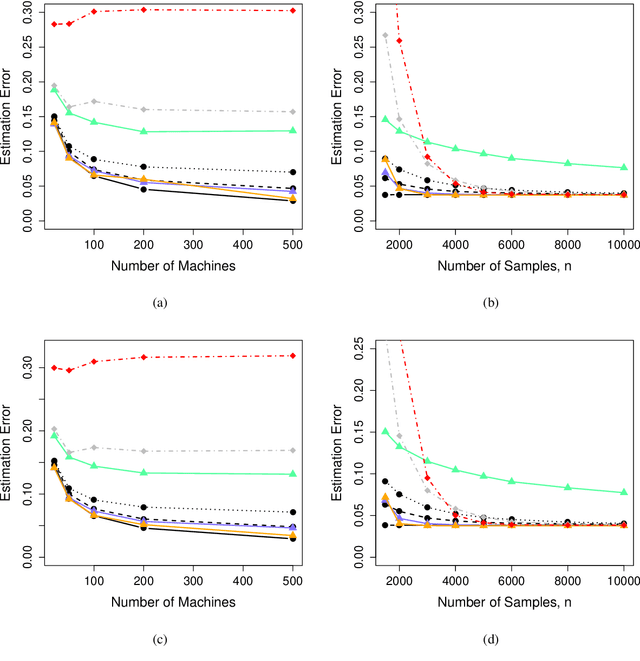

We address the problem of how to achieve optimal inference in distributed quantile regression without stringent scaling conditions. This is challenging due to the non-smooth nature of the quantile regression loss function, which invalidates the use of existing methodology. The difficulties are resolved through a double-smoothing approach that is applied to the local (at each data source) and global objective functions. Despite the reliance on a delicate combination of local and global smoothing parameters, the quantile regression model is fully parametric, thereby facilitating interpretation. In the low-dimensional regime, we discuss and compare several alternative confidence set constructions, based on inversion of Wald and score-type tests and resam-pling techniques, detailing an improvement that is effective for more extreme quantile coefficients. In high dimensions, a sparse framework is adopted, where the proposed doubly-smoothed objective function is complemented with an $\ell_1$-penalty. A thorough simulation study further elucidates our findings. Finally, we provide estimation theory and numerical studies for sparse quantile regression in the high-dimensional setting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge