Selection Bias Correction and Effect Size Estimation under Dependence
Paper and Code
Mar 28, 2015
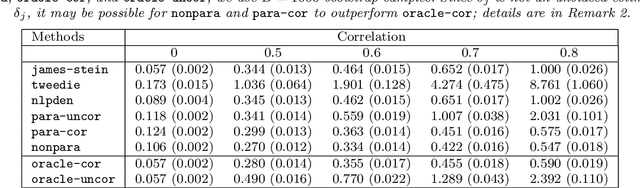

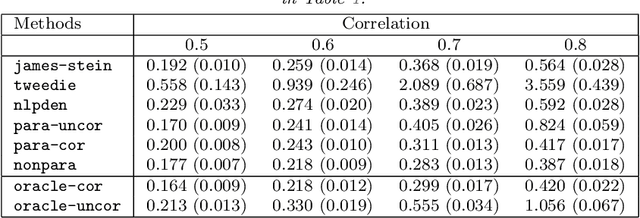
We consider large-scale studies in which it is of interest to test a very large number of hypotheses, and then to estimate the effect sizes corresponding to the rejected hypotheses. For instance, this setting arises in the analysis of gene expression or DNA sequencing data. However, naive estimates of the effect sizes suffer from selection bias, i.e., some of the largest naive estimates are large due to chance alone. Many authors have proposed methods to reduce the effects of selection bias under the assumption that the naive estimates of the effect sizes are independent. Unfortunately, when the effect size estimates are dependent, these existing techniques can have very poor performance, and in practice there will often be dependence. We propose an estimator that adjusts for selection bias under a recently-proposed frequentist framework, without the independence assumption. We study some properties of the proposed estimator, and illustrate that it outperforms past proposals in a simulation study and on two gene expression data sets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge